चित्र में, ABCD एक समांतर चतुर्भुज है। सिद्ध कीजिए कि
ar(ΔBCP)=ar(ΔDPQ)
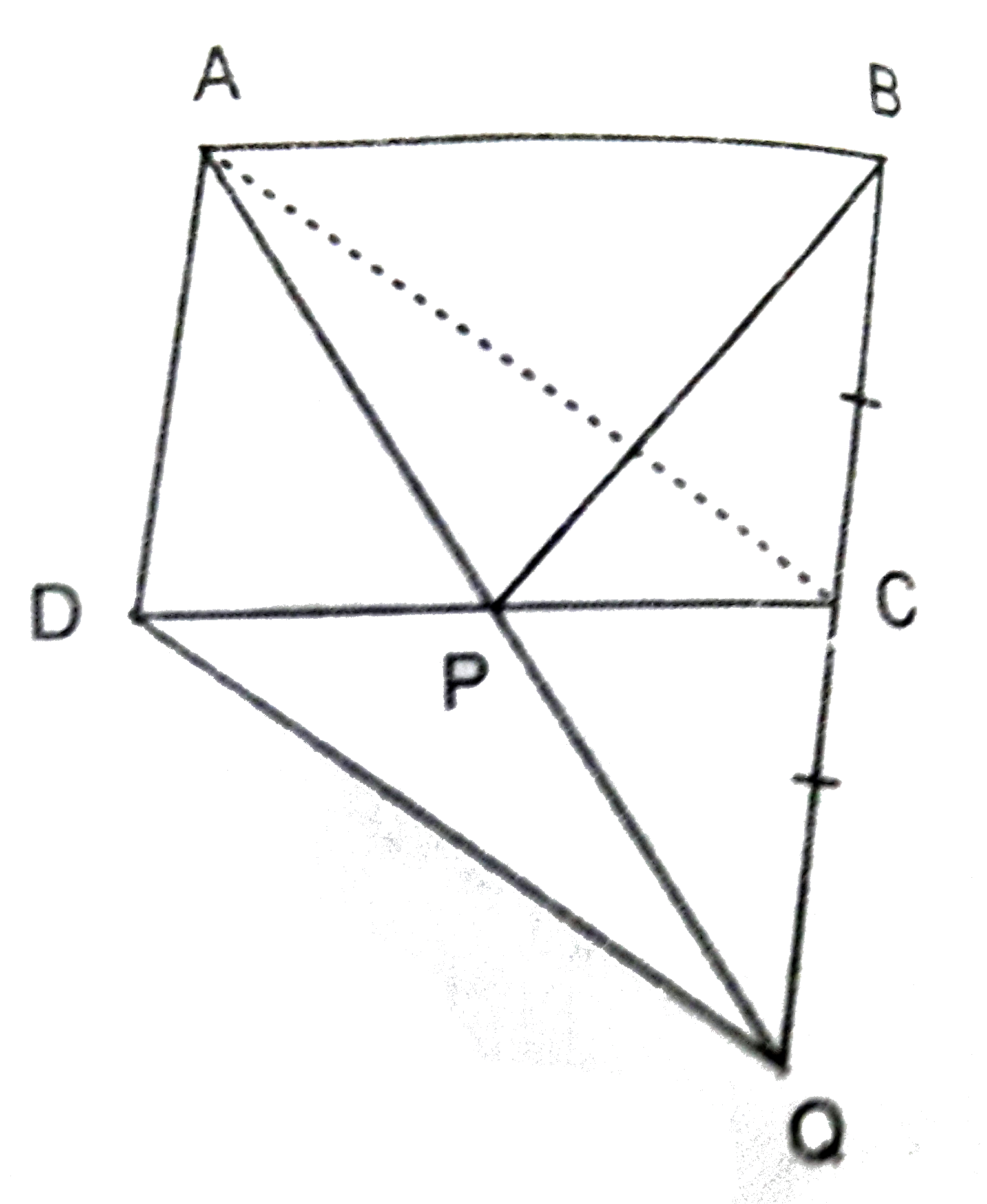
रचना : AC को मिलाइये ।
उपपत्ति : चूँकि ΔAPC तथा ΔBPC एक ही आधार PC पर तथा समान समांतर रेखाओं PC तथा AB के बीच स्थित है।
∴ar(ΔAPC)=ar(ΔBPC) ...(i)
अब ABCD एक समांतर चतुर्भुज है ।
⇒AD=BC
⇒AD=CQ [∵BC=CQ (दिया है)]
चूँकि AD || CQ तथा AD = CQ.
अतः चतुर्भुज mkADQC में सम्मुख भुजाओं का एक युग्म बराबर तथा समांतर है।
∴ ADQC एक समान्तर चतुर्भुज है।
⇒AP=PQ तथा CP=DP [∵||gm के विकर्ण परस्पर समद्विभाजित होते है। ]
अब ΔAPC तथा ΔDPQ में
AP=PQ [ ऊपर सिद्ध किया है]
∠APC=∠DPQ [शीर्षाभिमुख कोण]
तथा PC=PD
अतः भुजा-कोण-भुजा सर्वांगसमता कसौटी से
ΔAPC≅ΔDPQ
⇒ar(ΔAPC)=ar(ΔDPQ)...(ii) [∴ सर्वांगसमता त्रिभुजों के क्षेत्रफल बराबर होते है]
(i ) तथा (ii ) से
ar(ΔBCP)=ar(ΔDPQ)
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण1videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.16videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न8videos
संख्यिकीय आंकड़ों का आलेखीय निरूपण
- BOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न17videos
सर्वांगसम त्रिभुजें
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)
 05:04View Solution
05:04View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :
 06:36View Solution
06:36View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
12:33View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
04:36View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
10:35View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
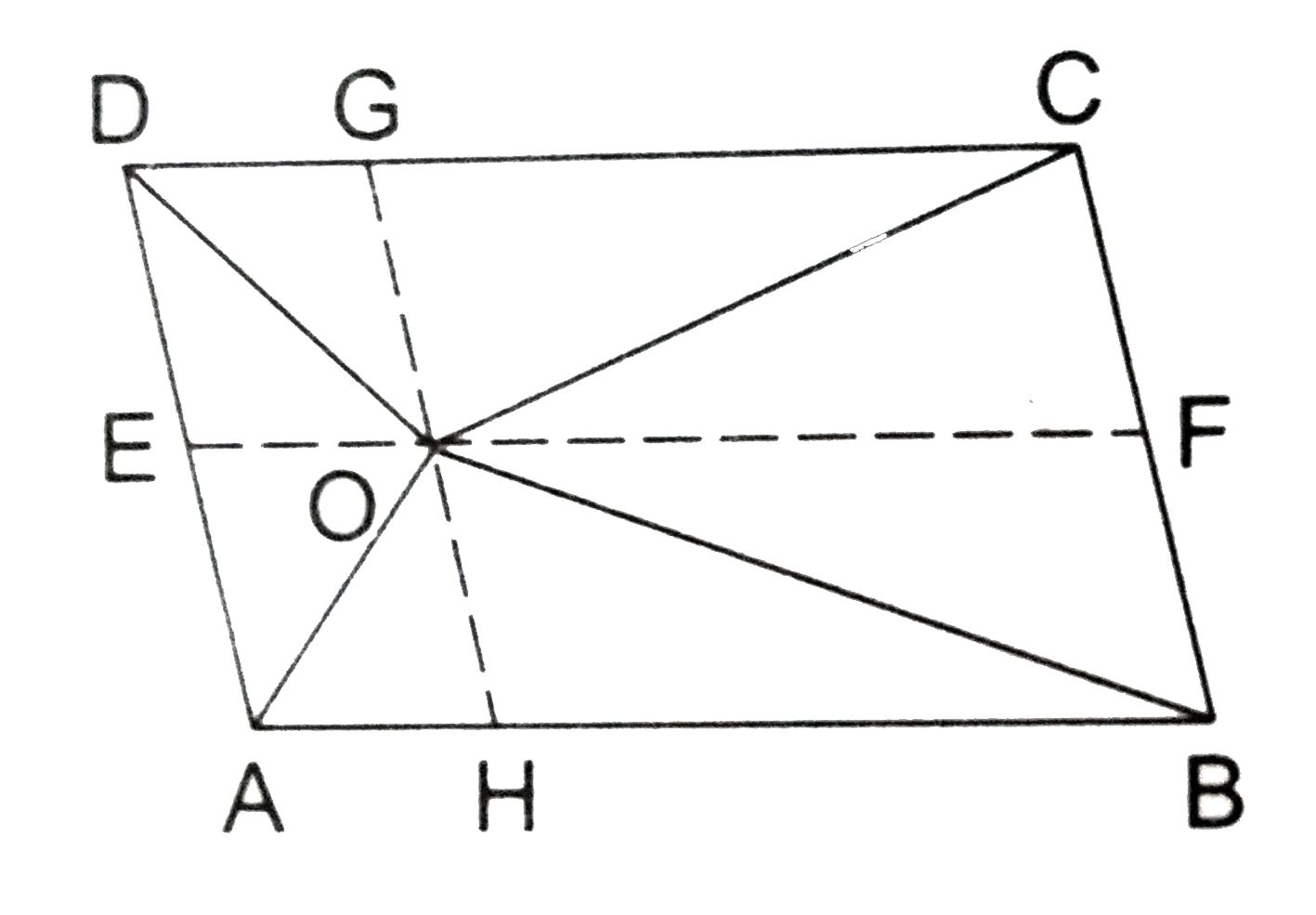 04:23View Solution
04:23View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)02:46View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)04:27View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
 04:11View Solution
04:11View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
02:48View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
02:51View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
02:56View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
10:01View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.03:05View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
03:13View Solution

