If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
zero
−5E0x0
−3E0x0
−√5E0x0
The correct Answer is:B
A in (0, 0) and B is (x0,2x0)
VB−VA=−∫BA→E.d→s
⇒VB=−∫BA→E.decs
→E=E0ˆi+2E0ˆj
d→s=dxˆi+dyˆj
∫(x0,2x0)(0,0)→E.d→s=∫x0,2x00,0(E0ˆi+2E0ˆj)⋅(dxˆi+dyˆj)
⇒VB=−5E0x0
Topper's Solved these Questions
Similar Questions
An electric field →E=(25ˆi+30ˆj)NC−1 exists in a region of space.If the potential at the origin is taken to be zero then the potential at x=2 m y=2 m is :?
View SolutionLet there be a uniform electric field "E" existing along the positive X-direction.Assume electric potential to be zero at the origin.Potential at the point x=x0 is
View Solution
Knowledge Check
If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
AzeroB−E0x0C−2E0x0D−√5E0x0If electric potential is zero, the →E are:
AzeroBnot zeroCinsufficient formationD∞In a region where E = 0, the potential (V) varies with distance r as -
AVα1rBVαrCVα1r2DV = const. independent of (r )
An electric field E=(20ˆi+30ˆj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionElectric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
View SolutionConisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
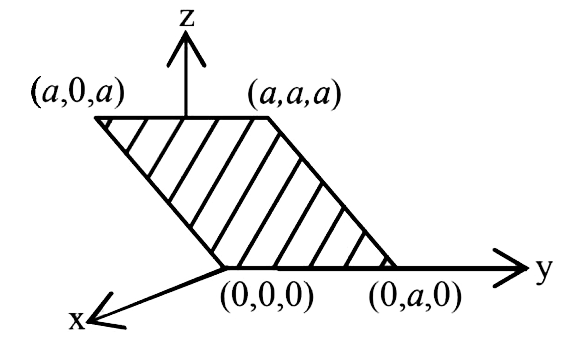
View SolutionAn electric field →E=20yˆj exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
View SolutionA unifrom electric field having a magnitude E0 and direction along the positive X-axis exists. If the protential V is zero at x=0, then its value at X=+x will be
View Solution
