Electric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
It moves along helix with constant pitch
It moves along circular path in Y Z plane
It moves along helix with increasing pitch
It moves along helix with decreasing pitch
The correct Answer is:C
To solve the problem, we need to analyze the motion of a charged particle projected in the presence of both an electric field and a magnetic field. Here's a step-by-step solution:
Step 1: Understand the Forces Acting on the Charge
The charged particle experiences two forces:
1. Electric Force (→FE): This force is given by →FE=q→E, where q is the charge and →E=E0^i is the electric field.
2. Magnetic Force (→FB): This force is given by →FB=q(→v×→B), where →B=B0^i is the magnetic field and →v=v0^j is the velocity of the charge.
Step 2: Calculate the Electric Force
The electric force acting on the charge is:
→FE=qE0^i
This force acts in the direction of the electric field, which is along the ^i direction.
Step 3: Calculate the Magnetic Force
The magnetic force can be calculated using the cross product:
→FB=q(→v×→B)=q(v0^j×B0^i)
Using the right-hand rule, we find:
^j×^i=−^k⇒→FB=−qv0B0^k
This force acts in the negative ^k direction.
Step 4: Determine the Resultant Force
The total force acting on the charge is the vector sum of the electric and magnetic forces:
→F=→FE+→FB=qE0^i−qv0B0^k
Step 5: Analyze the Motion
The charge will experience:
- An acceleration in the ^i direction due to the electric force.
- A circular motion in the ^j and ^k plane due to the magnetic force.
Step 6: Describe the Path of the Charge
The charge will move in a helical path because:
- The electric field causes a constant acceleration in the ^i direction, which increases the velocity in that direction.
- The magnetic field causes circular motion in the ^j and ^k plane.
Since the velocity in the ^i direction is increasing due to the electric field, the pitch of the helix (the distance between successive turns) will also increase.
Conclusion
The correct description of the motion of the charge is that it moves along a helix with increasing pitch.
---
The charged particle experiences two forces:
1. Electric Force (→FE): This force is given by →FE=q→E, where q is the charge and →E=E0^i is the electric field.
2. Magnetic Force (→FB): This force is given by →FB=q(→v×→B), where →B=B0^i is the magnetic field and →v=v0^j is the velocity of the charge.
The electric force acting on the charge is:
→FE=qE0^i
This force acts in the direction of the electric field, which is along the ^i direction.
The magnetic force can be calculated using the cross product:
→FB=q(→v×→B)=q(v0^j×B0^i)
Using the right-hand rule, we find:
^j×^i=−^k⇒→FB=−qv0B0^k
This force acts in the negative ^k direction.
The total force acting on the charge is the vector sum of the electric and magnetic forces:
→F=→FE+→FB=qE0^i−qv0B0^k
The charge will experience:
- An acceleration in the ^i direction due to the electric force.
- A circular motion in the ^j and ^k plane due to the magnetic force.
The charge will move in a helical path because:
- The electric field causes a constant acceleration in the ^i direction, which increases the velocity in that direction.
- The magnetic field causes circular motion in the ^j and ^k plane.
The correct description of the motion of the charge is that it moves along a helix with increasing pitch.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE - 3
Explore 29 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
Electric field and magnetic field in a region of space are given by(Ē=E0ˆj). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass in and charge q is given a velocity v=v−0ˆj+v−0ˆk. Find the minimum speed of the particle and the time when it happens so.

View Solution
Knowledge Check
Electric field strength ¯¯¯E=E0ˆi and ¯¯¯B=B0ˆi exists in a region. A charge is projected with a velocity ¯v=v0ˆj at origin , then
AIt moves along helix with constant pitchBIt moves along circular path in YZ planeCIt moves along helix with increasing pitchDIt moves along helix with decreasing pitchIn the region between the plane z=0 and z=a(a>0), the uniform electric and magnetic fields are given by →E=E0(ˆk−ˆj), →B=B0ˆi. The region defined by a≤z≤b contains only magnetic field →B=−B0ˆi. Beyond z>b no field exits. A positive point charge q is projected from the origin with velocity v0ˆk. Assuming the mass of the particle to be 23qE0av20.
The value of E0 such that the particle moves undeviated upto the plane z=a is
 Av0B0√2Bv0B0Cv0B0√2Dv0B02
Av0B0√2Bv0B0Cv0B0√2Dv0B02In the region between the plane z=0 and z=a(a>0), the uniform electric and magnetic fields are given by →E=E0(ˆk−ˆj), →B=B0ˆi. The region defined by a≤z≤b contains only magnetic field →B=−B0ˆi. Beyond z>b no field exits. A positive point charge q is projected from the origin with velocity v0ˆk. Assuming the mass of the particle to be 23qE0av20.
When the particle just reverse its direction, all the fields are switched off. Time taken by the particle to touch the plane z=0 from that instant is
 Aa/v0Ba/2v0Ca3v0Da4v0
Aa/v0Ba/2v0Ca3v0Da4v0
If a particle of charge 1μC is projected into a magnetic field →B=(2ˆi+yˆj–zˆk)T with a velocity →V=(4ˆi+2ˆj−6ˆk)ms−1 , then it passes undeviated. If it is now projected with a velocity →V=ˆi+ˆj , then find the force experienced by it
View SolutionIn the region between the plane z=0 and z=a(a>0), the uniform electric and magnetic fields are given by →E=E0(ˆk−ˆj), →B=B0ˆi. The region defined by a≤z≤b contains only magnetic field →B=−B0ˆi. Beyond z>b no field exits. A positive point charge q is projected from the origin with velocity v0ˆk. Assuming the mass of the particle to be 23qE0av20.
The minimum value of b such that the particle reverses its direction completely is
View SolutionIf uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
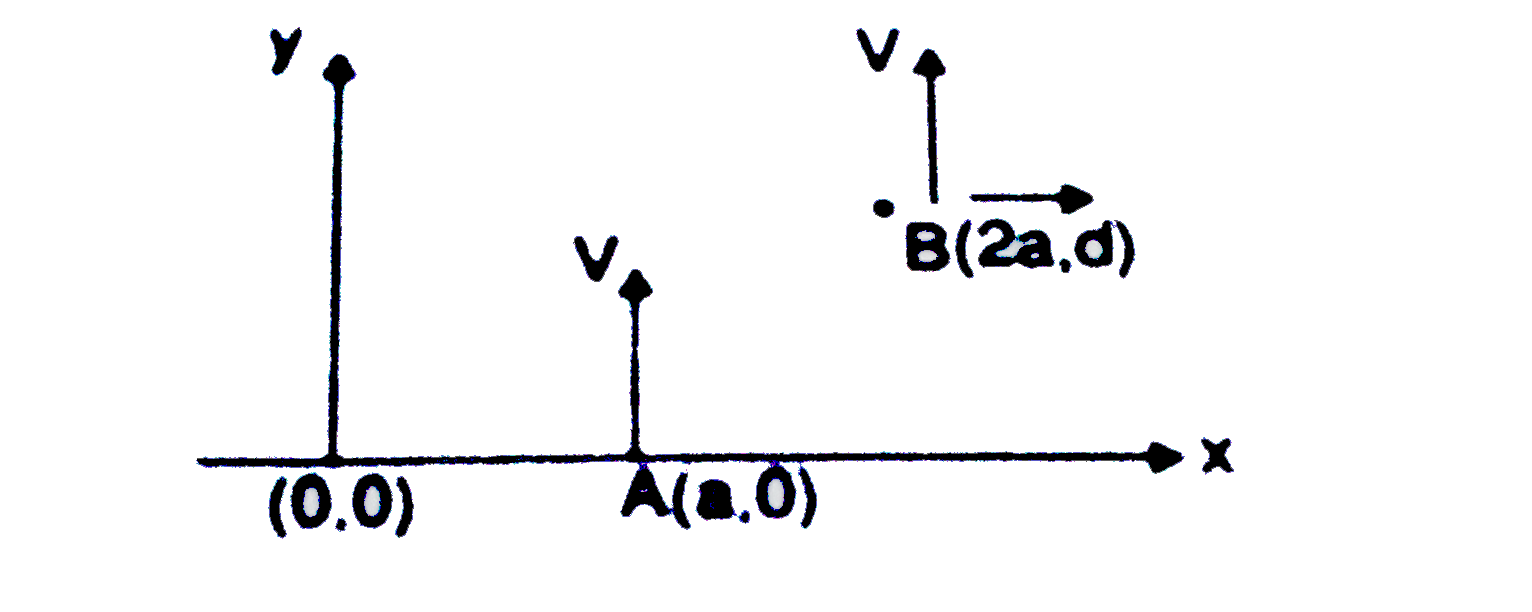
View SolutionA uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
View SolutionA particular region contains uniform electric and magnetic fields, →E=E0ˆiand→B=B0ˆi respectively. When a particle having mass and charge m and q respectively, enters the region with velocity →v=v0ˆj, it is observed that the speed of the particle becomes 2v0 after a time t. Find the value of t.
View Solution