A radioactive nucleus X converts into nucleus Y by emitting B+. If atomic masses of X and Y are MX and MY then Q value of reaction will be :-
Q=MxC2
Q=(MX−MY−Me)C2
Q=(MX−MY)C2
Q=(MX−MY−2me)C2
The correct Answer is:A
Step by step video & text solution for A radioactive nucleus X converts into nucleus Y by emitting B^+. If atomic masses of X and Y are M_X and M_Y then Q value of reaction will be :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A radioactive nucleus A at rest disintegrates into two nuclei B and C. Mass of B is 12m and that of C is 4m .The Q-value of the reaction is Q=h224mλ2 .The energy liberated in reaction is completely imparted to the products (B and C) as kinetic energy.
View SolutionA heavy nucleus of mass Mx decay into two nuclei (Y and Z) of masses Myand Mz . The Q value of the reaction is
View Solution
Knowledge Check
A nucleus 220X at rest decays emitting an α-particle . If energy of daughter nucleus is 0.2 MeV, Q value of the reaction is
A10.8 MeVB10.9 MeVC11 MeVD11.1 MeVA radioactive nucleus .92X235 decays to .91Y231. Which of following particles are emitted ?
AOne alpha and one electronBTwo deutrons and one positionCOne alpha and one protonDOne proton and four neutronsThe radioactive nucleus of an element X decays to a stable nucleus of element Y.A graph of the rate of romation of Y against time would look like:
A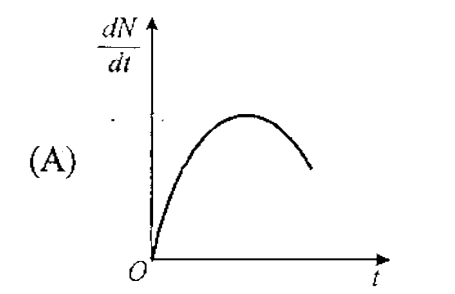 B
B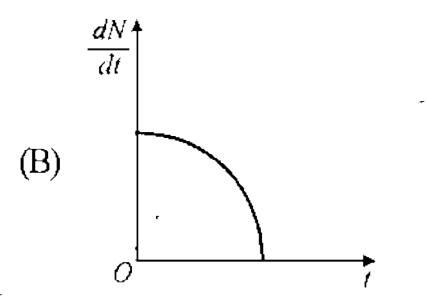 C
C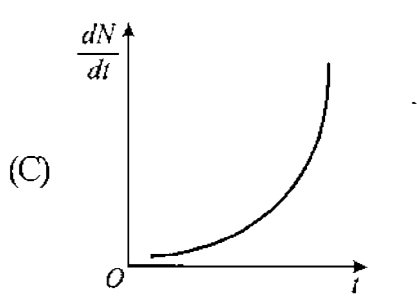 D
D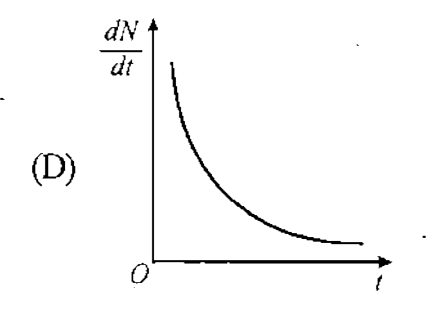
A radioactive isotope X decays into a stable nucleus Y. Draw graphs showing the variation of rate of formation of Y versus time and the variation of population of Y versus time. Initial population of Y is zero.
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View SolutionTwo radio active nuclei X and Y decay into stable nucleus Z
X→Z+2α+β−
Y→Z+α+2β+
if Z1 and Z2 are atomic numbers of X and Y then
View SolutionA radioactive nucleus [initial mass number A and atomic number Z] emits 3 α-particles and 2 positrons. The ratio of number of neutrons to that of protons in the final nucleus will be
View SolutionA radioactive nucleus (initial mass number A and atomic number Z) emits 3α-particles and 2 positrons. The ratio of number of neutrons to that of protons in the final nucleus will be
View Solution
