If P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
To prove that R2+S2=2(P2+Q2) given the equations P+Q=R and P−Q=S, we can follow these steps:
Step 1: Express R2 and S2 in terms of P and Q
Using the definitions of R and S:
R=P+QandS=P−Q
We can find R2 and S2:
R2=(P+Q)⋅(P+Q)=P2+2(P⋅Q)+Q2
S2=(P−Q)⋅(P−Q)=P2−2(P⋅Q)+Q2
Step 2: Add R2 and S2
Now, we add R2 and S2:
R2+S2=(P2+2(P⋅Q)+Q2)+(P2−2(P⋅Q)+Q2)
Step 3: Simplify the expression
When we combine the terms, we notice that the 2(P⋅Q) and −2(P⋅Q) cancel each other out:
R2+S2=P2+Q2+P2+Q2=2P2+2Q2
Step 4: Final result
Thus, we can conclude:
R2+S2=2(P2+Q2)
This completes the proof.
R=P+QandS=P−Q
R2=(P+Q)⋅(P+Q)=P2+2(P⋅Q)+Q2
S2=(P−Q)⋅(P−Q)=P2−2(P⋅Q)+Q2
R2+S2=(P2+2(P⋅Q)+Q2)+(P2−2(P⋅Q)+Q2)
R2+S2=P2+Q2+P2+Q2=2P2+2Q2
R2+S2=2(P2+Q2)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Example39videos
VECTORS
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - check point 2.115videos
VECTORS
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Single Correct39videos
VECTORS
- BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery32videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
If 3P = 2Q and 2Q = 3R, then what is P : Q : R?
A6:9:1B2:3:2C4:6:9D4:6:1
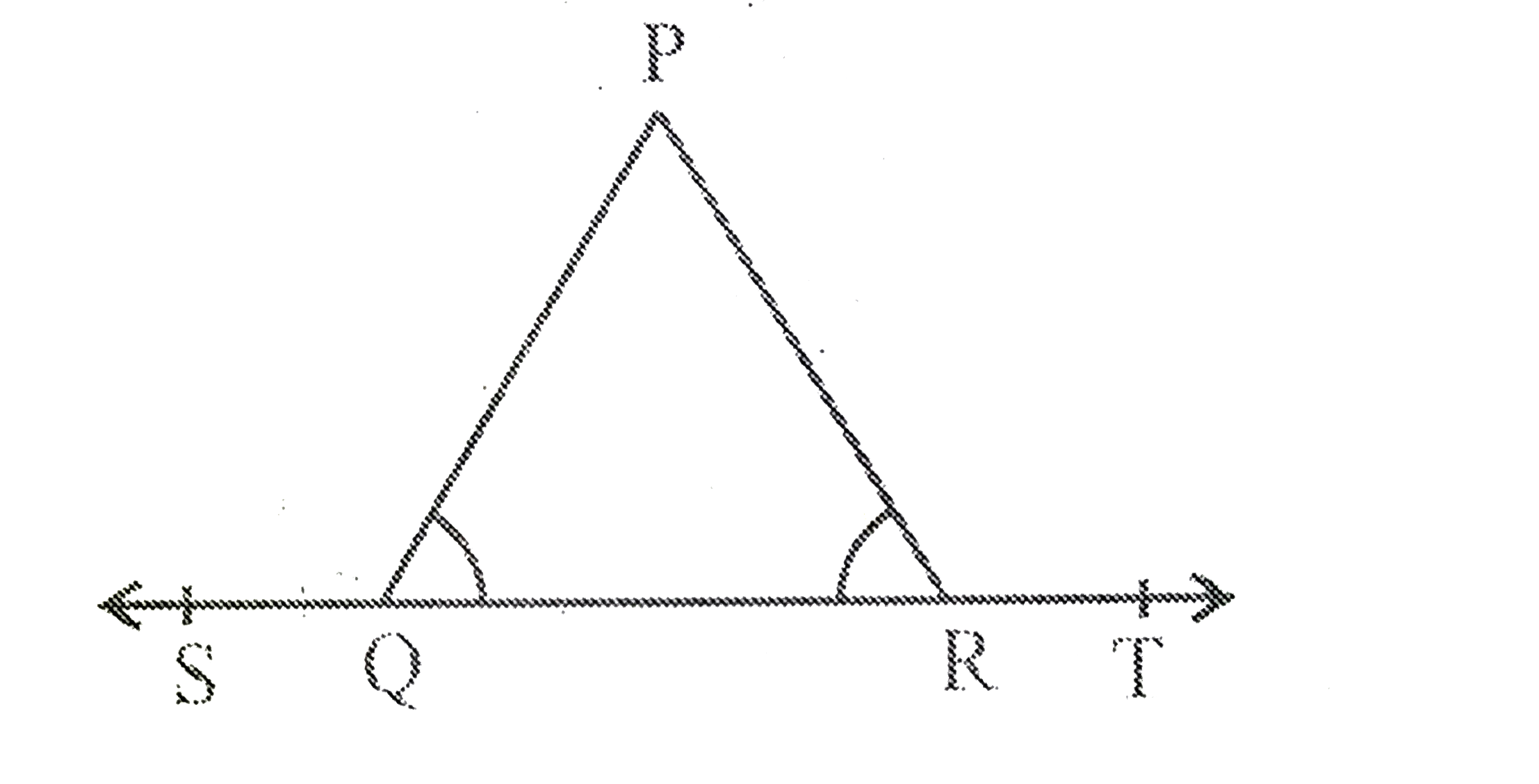
In Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 View Solution
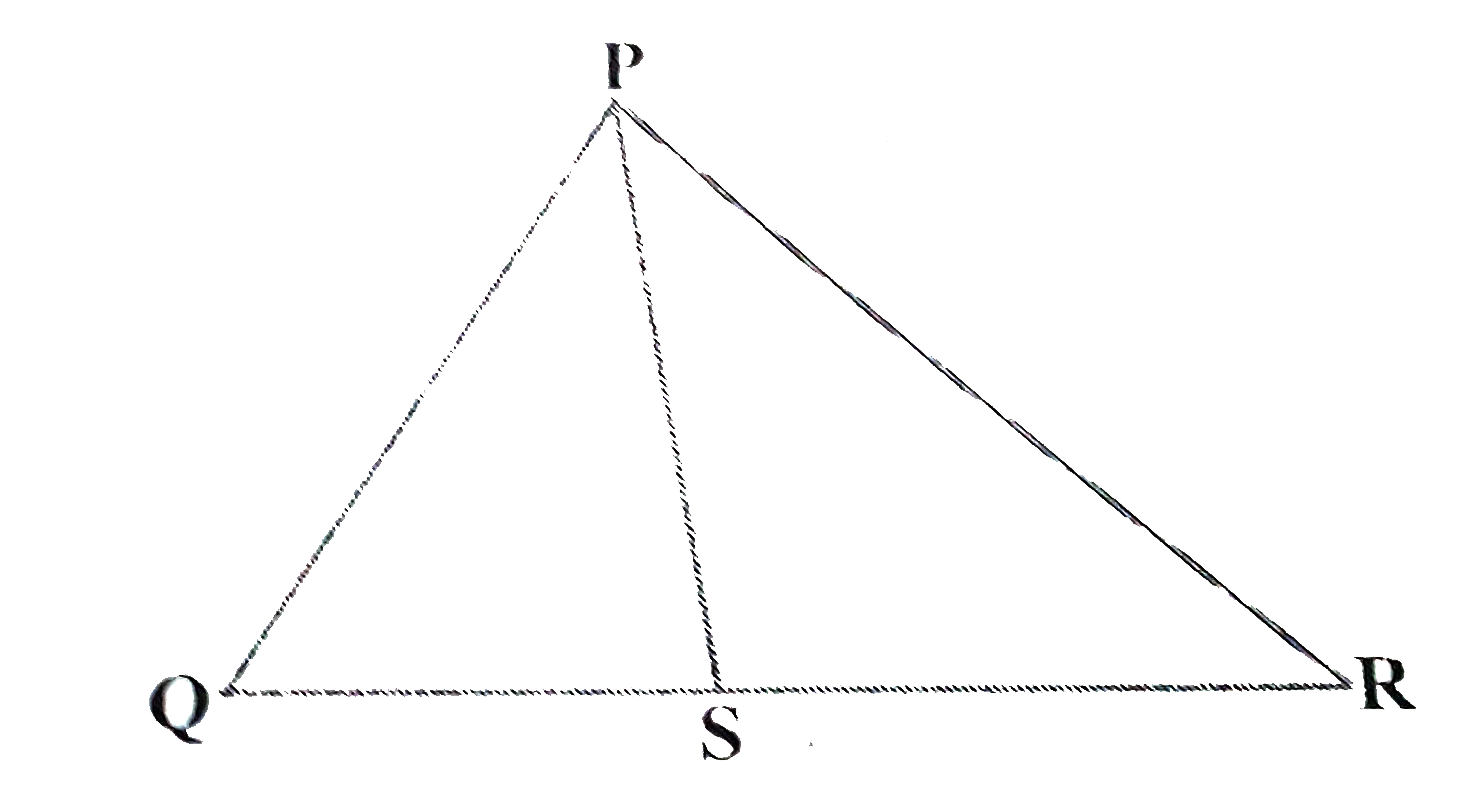
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
 View Solution
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIf p = -2, q = - 1 and r = 3, find the value of
(i) p2+q2−r2
(ii) 2p2−q2+3r2
(iii) p - q - r
(iv) p3+q3+r3+3pqr
(v) 3p2q+5pq2+2pqr
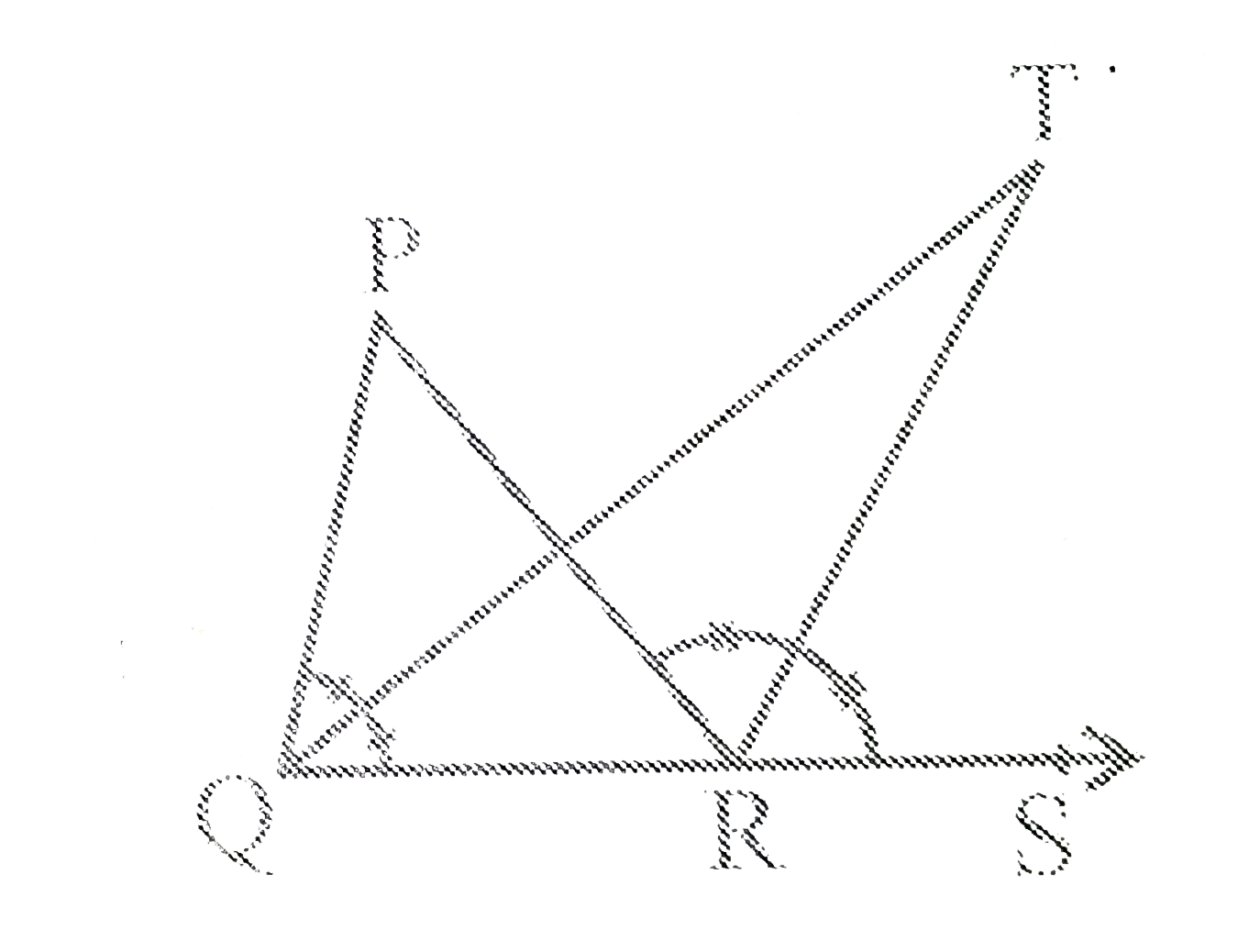
(vi) p4+q4−r4View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
 View Solution
View SolutionIn the given Fig. , if QTPR=QRQS and ∠1=∠2 . Prove that PQS~TQR . (FIGURE)
View Solution


