Equation of motion of a body is dvdt=−4v+8, where v is the velocity in ms−1 and t is the time in second. Initial velocity of the particle was zero. Then,
the initial rate of change of acceleration of the particle is 8ms−2
the terminal speed is 2ms−1
Both (a) and (b) are correct
Both (a) and (b) are wrong
The correct Answer is:B
dvdt=a=−44v+8
∴dadt=−4dvdt
=−4(−4v+8)
=16v−32
∴(dadt)i=16vi−32
=(16)(0)−32
=−32m/s2
Further, ∫v0dv8−4v=∫t0dt
Solving this equation we get,
v=2(1−e−4t)
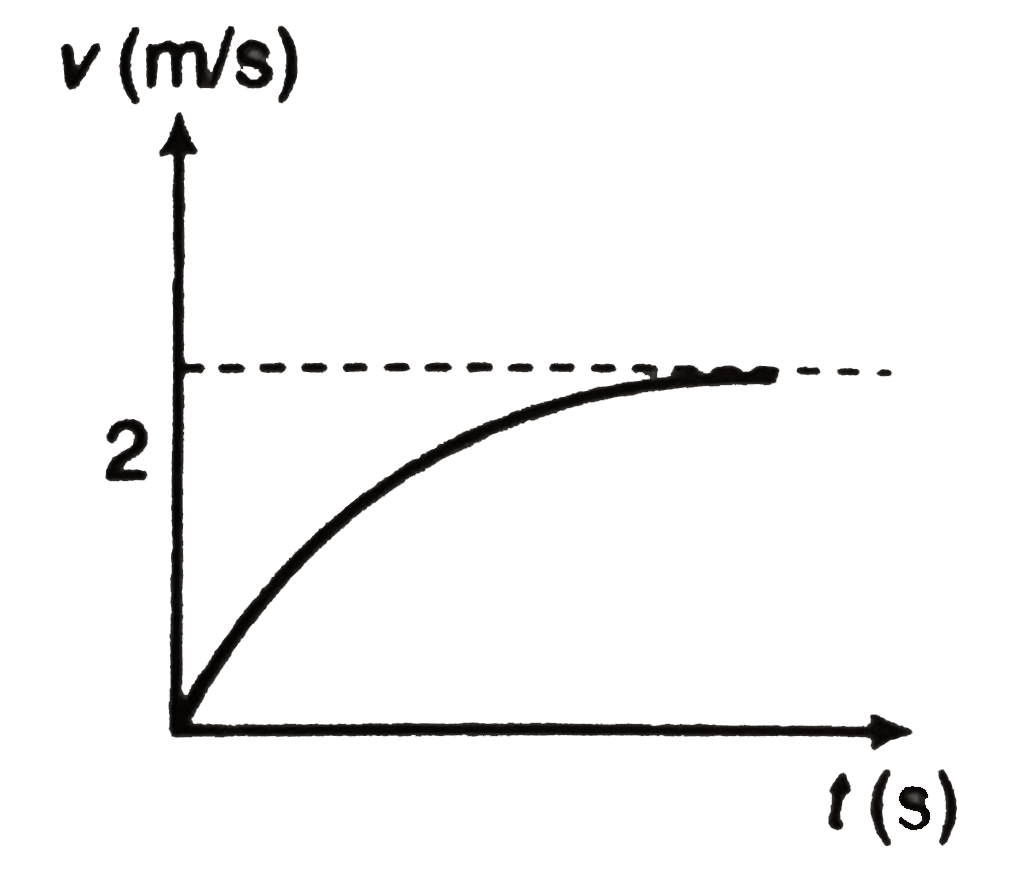
Hence, v-t graph is exponentially incresing graph,
terminating at 2 m//s.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionThe motion of a body is given by the equation dvdt=4−2v, where v is the speed in m/s and t in second. If the body was at rest at t = 0, then find
(i) The magnitude of initial acceleration
(ii) Speed of body as a function of time
View Solution
Knowledge Check
The motion of a particle moving along x-axis is represented by the equation dvdt=6−3v, where v is in m/s and t is in second. If the particle is at rest at t = 0 , then
AThe speed of the particle in 2 /s when the acceleration of particle is zeroBAfter a long time the particle moves with a constant velocity of 2 m/sCThe speed is 0.1 m/s, when the acceleration is half of its initial valueDThe magnitude of final acceleration is 6m/s2An equation relating to stability of an aeroplane is dvdt=gcosα−kv, where v is the velocity and g, k,α are constantts. If v=0. at t=0, velocity is
Agcosαk(1−e−kt)B−gcosαk(1−e−kt)Cgcosαk(1−ekt)D−gcosαk(1−ekt)A particle moving in a straight in a straight line has velocity and displacement equation as
v=4√1+s,
where v is in m/s and s is in m. The initial velocity of the particle is:A4 m/sB16 m/sC2 m/sDzero
A body moves so that it follows the following relation dvdt=−v2+2v−1 where v is speed in m/s and t is time in second. If at t=0, v=0 then find the speed (in m/s) when acceleration in one fourth of its initial value.
View SolutionA particle is moving in a straight line such that dv/dt=−λv, where v is the velocity and λ is a constant. At t=0, the particle is at the origin and moves with velocity v0. Sketch the following graphs:
(a)v−t(b)s−t(c)v−s(d)logevv/st
View SolutionAn equation relating to the stability of an aeroplane is given by dvdt=gcosα−kv, where v is the velocity and g,α,k are constants. Find an expression for the velocity if v=0 at t=0
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionThe law of motion of a particle is S=tn, where n≥3.If v is the velocity and a the acceleration at time t, then aSv2=
View Solution
