A particle is moving along a straight line. The displacement of the particle becomes zero in a certain time (t>0). The perticle does not undergo any collision.
The acceleration of the particle may be zero always
The acceleration of the particle may be zero uniform
The velocity of the particle must be zero at some instant
The acceleration of the particle must change its direction
The correct Answer is:B, C
To solve the problem, we need to analyze the motion of the particle given that its displacement becomes zero after a certain time t (where t>0).
1. Understanding Displacement:
- Displacement is defined as the change in position of an object. If the displacement is zero after a certain time, it means that the particle has returned to its original position.
2. Analyzing Motion:
- Since the particle returns to its starting point, it must have moved away from that point and then come back. This implies that at some point during its motion, the particle must have stopped momentarily before reversing direction.
3. Velocity Consideration:
- For the particle to return to its original position, its velocity must be zero at some instant. This is because, to change direction, an object must first come to a stop. Therefore, the velocity of the particle must be zero at some point during its motion.
4. Acceleration Consideration:
- The acceleration of the particle can vary. It is possible for the particle to have zero acceleration at some points (for example, if it moves with constant velocity), but it can also have non-zero acceleration when it is speeding up or slowing down. Thus, while the acceleration may be zero at certain times, it is not necessarily always zero.
5. Direction of Acceleration:
- The statement regarding the acceleration changing direction is not necessarily true. The acceleration can remain in the same direction or change direction depending on the motion of the particle. Therefore, it is incorrect to assert that the acceleration must change direction.
Conclusion:
Based on the analysis:
- The velocity of the particle must be zero at some instant (Correct).
- The acceleration of the particle may be zero at some points but not always (Correct).
- The acceleration does not necessarily have to change direction (Incorrect).
Thus, the correct options are B and C.
- Displacement is defined as the change in position of an object. If the displacement is zero after a certain time, it means that the particle has returned to its original position.
- Since the particle returns to its starting point, it must have moved away from that point and then come back. This implies that at some point during its motion, the particle must have stopped momentarily before reversing direction.
- For the particle to return to its original position, its velocity must be zero at some instant. This is because, to change direction, an object must first come to a stop. Therefore, the velocity of the particle must be zero at some point during its motion.
- The acceleration of the particle can vary. It is possible for the particle to have zero acceleration at some points (for example, if it moves with constant velocity), but it can also have non-zero acceleration when it is speeding up or slowing down. Thus, while the acceleration may be zero at certain times, it is not necessarily always zero.
- The statement regarding the acceleration changing direction is not necessarily true. The acceleration can remain in the same direction or change direction depending on the motion of the particle. Therefore, it is incorrect to assert that the acceleration must change direction.
Based on the analysis:
- The velocity of the particle must be zero at some instant (Correct).
- The acceleration of the particle may be zero at some points but not always (Correct).
- The acceleration does not necessarily have to change direction (Incorrect).
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective45videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
A particle is moving along a straight line such that its displacement x and time t are related as follows:
x2=1+t2
Show that acceleration of the particle can be represented as: a=1x−t2x3.View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View Solution
Knowledge Check
- Question 1 - Select One
If a particle is moving along straight line with increasing speed, then
AIts acceleration is negativeBIts acceleration may be decreașingCIts acceleration is positiveDBoth (2) & (3) - Question 2 - Select One
For a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?A−9ms−1B−12ms−1C3ms−1D42ms−1 - Question 3 - Select One
A particle is moving along a straight line whose velocity - displacement graph is shown in figure. What is the acceleration when displacement is 3 m?
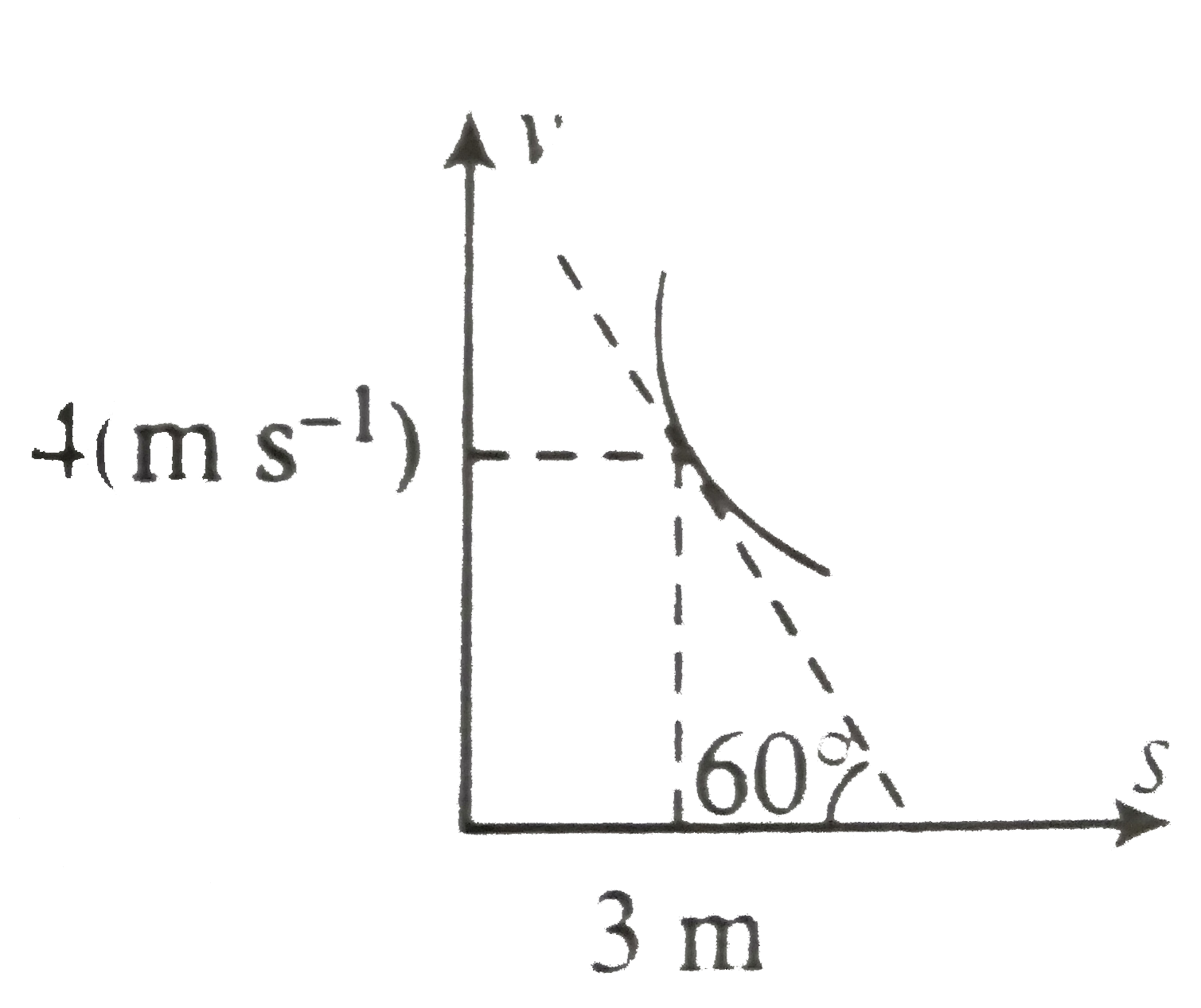 A−4√3ms−2B3√3ms−2C√3ms−2D4/√3ms−2
A−4√3ms−2B3√3ms−2C√3ms−2D4/√3ms−2
Acceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
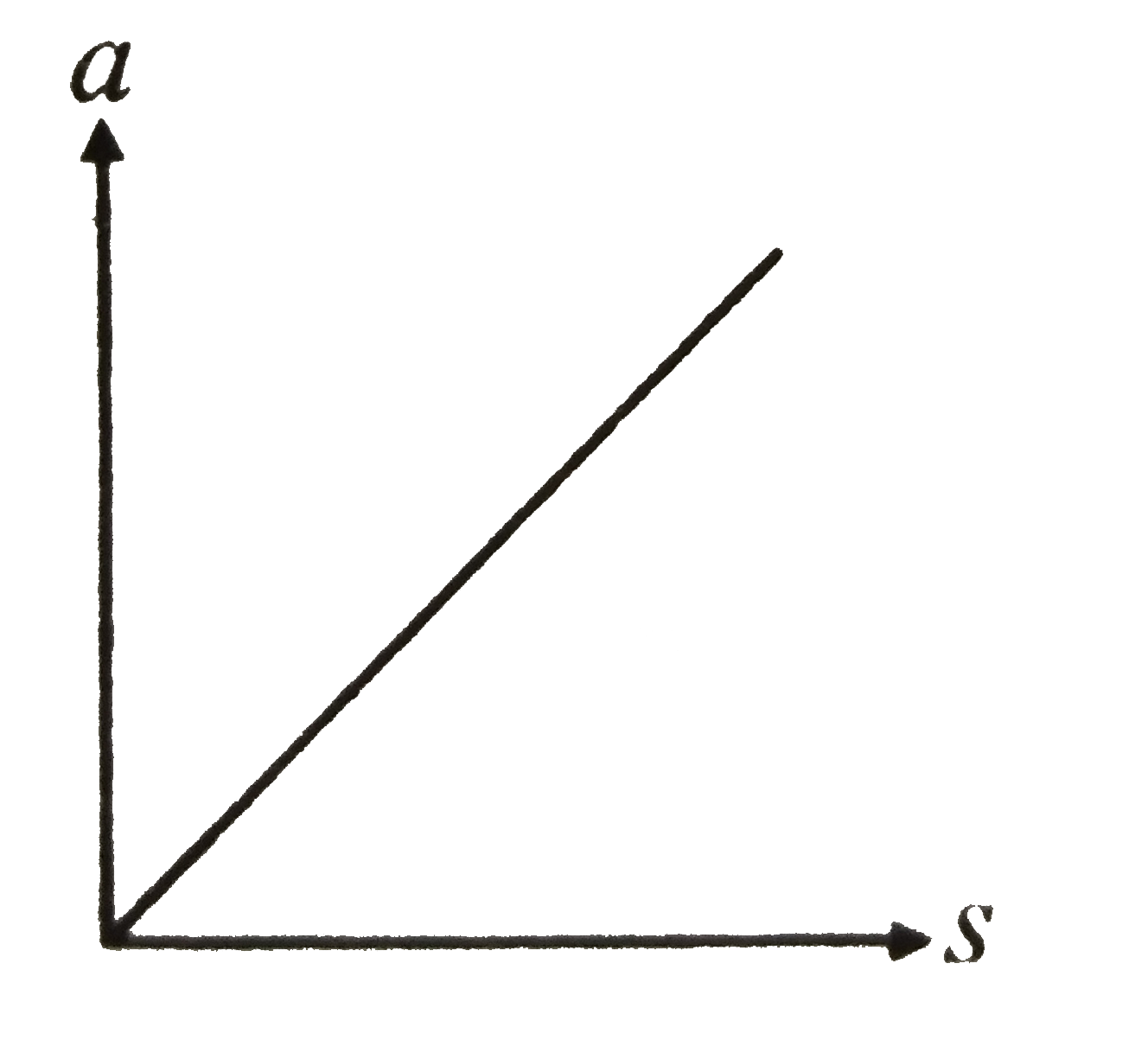 View Solution
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA particle is moving with a constant speed along a straight line path. A force is not requied to
View SolutionFor a particle moving in a straight line
View SolutionSTATEMENT-1: When a particle move along a straight line magnitude of its average velocity is equal to its average speed over any time interval provided particle does not return to path.
STATEMENT-2: For one dimensional motion displacement and distance both are same.View Solution

