An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would be
73.65 m
116.25 m
82.56m
63.25 m
The correct Answer is:C
If the ball does not collides, then it will reach its
maximum height in time, t0=ug=2510=2.5s
Since t<t0, therefore as per the question ball is at
its maximum height at 2.13s.
hmax=50+2+25×2.13−5×(2.13)2
=82.56m
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE
41 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
An elevator without a ceiling is ascending with a constant speed of 10 m//s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor. At this time the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m//s. (Take g=9.8m/s2)
(a) What maximum height above the ground does the ball reach?
(b) How long does the ball take to return to the elevator floor?
View SolutionAn elevator with floor to roof height 24m starts moving upwards with a constant acceleration of 2(m)/(s^(2)). At t=2s ,a bolt on the roof loosens and falls. Time the bolt takes to travel from the roof to the floor of the elevator is g=10ms^(-2)]
View Solution
Knowledge Check
An elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given byA2.13 sB2.0 sC1.0 sD3.12 sAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
4. The maximum separation between the floor of elevator and the ball during its flight would beA12 mB15 mC9.5 mD7.5 mAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would beA16.25 mB8.76 mC20.24 mD30.56 m
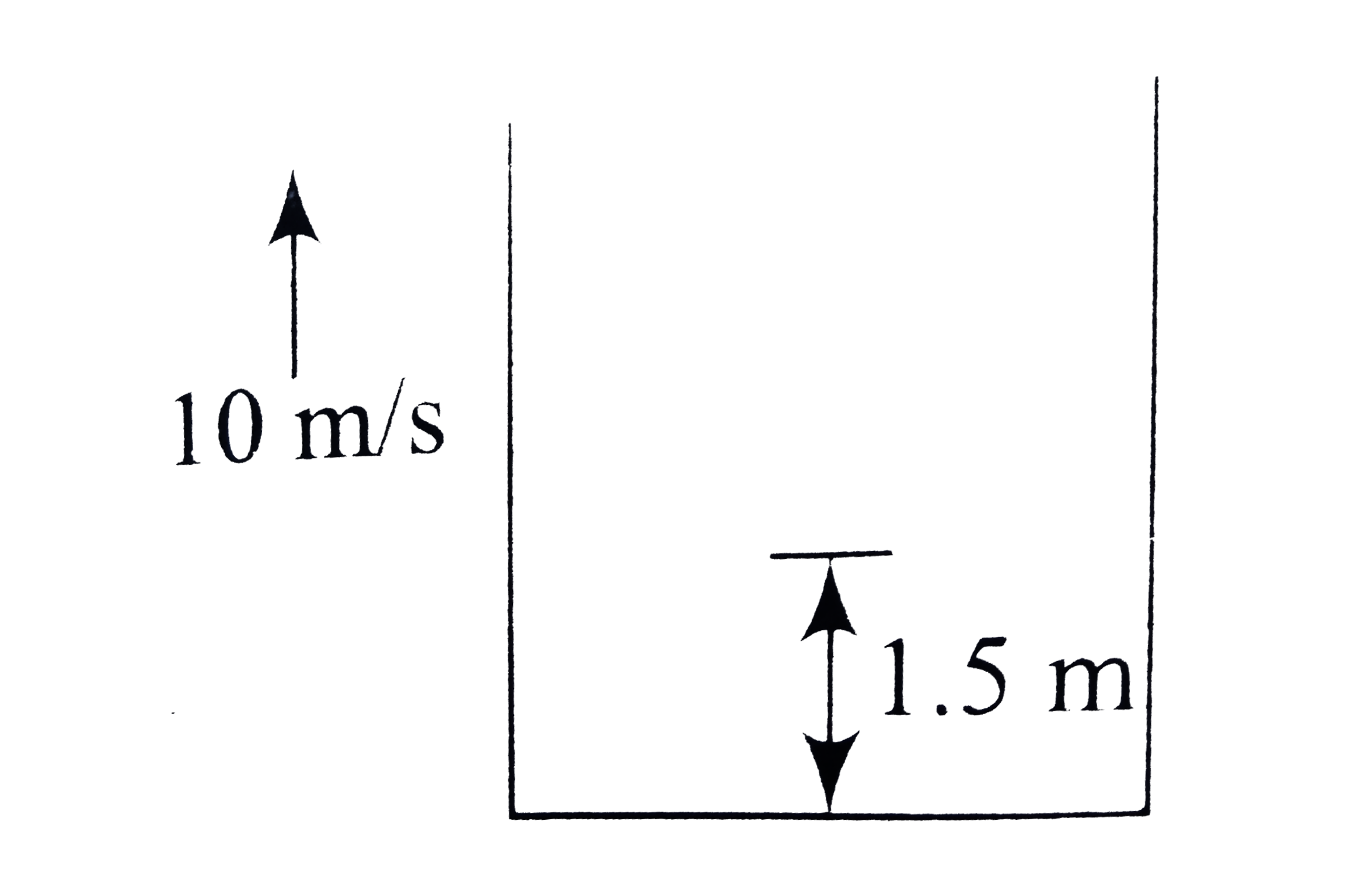
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View Solution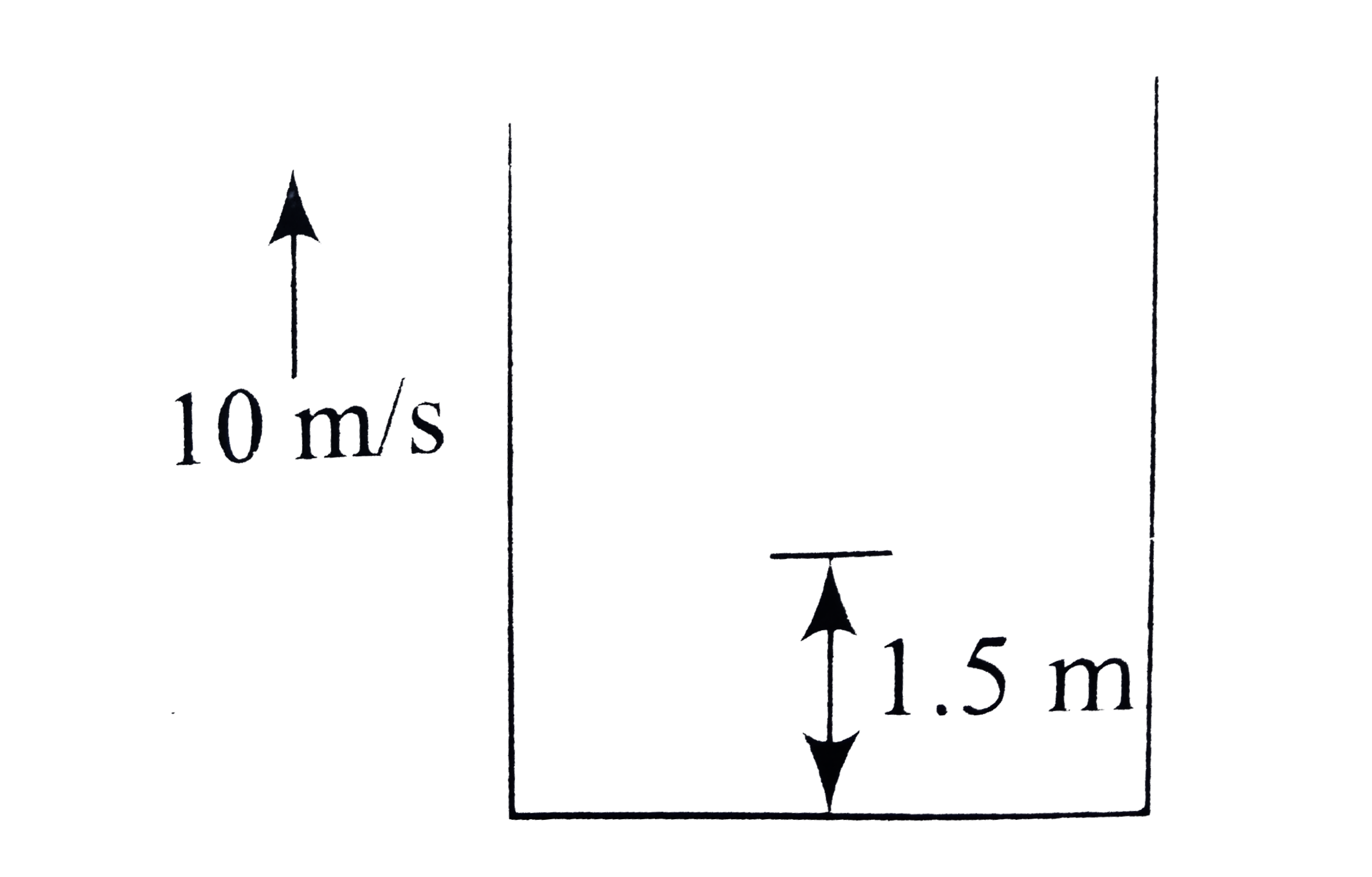
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the acceleration of the elevator in upward direction, (mss2):
View Solution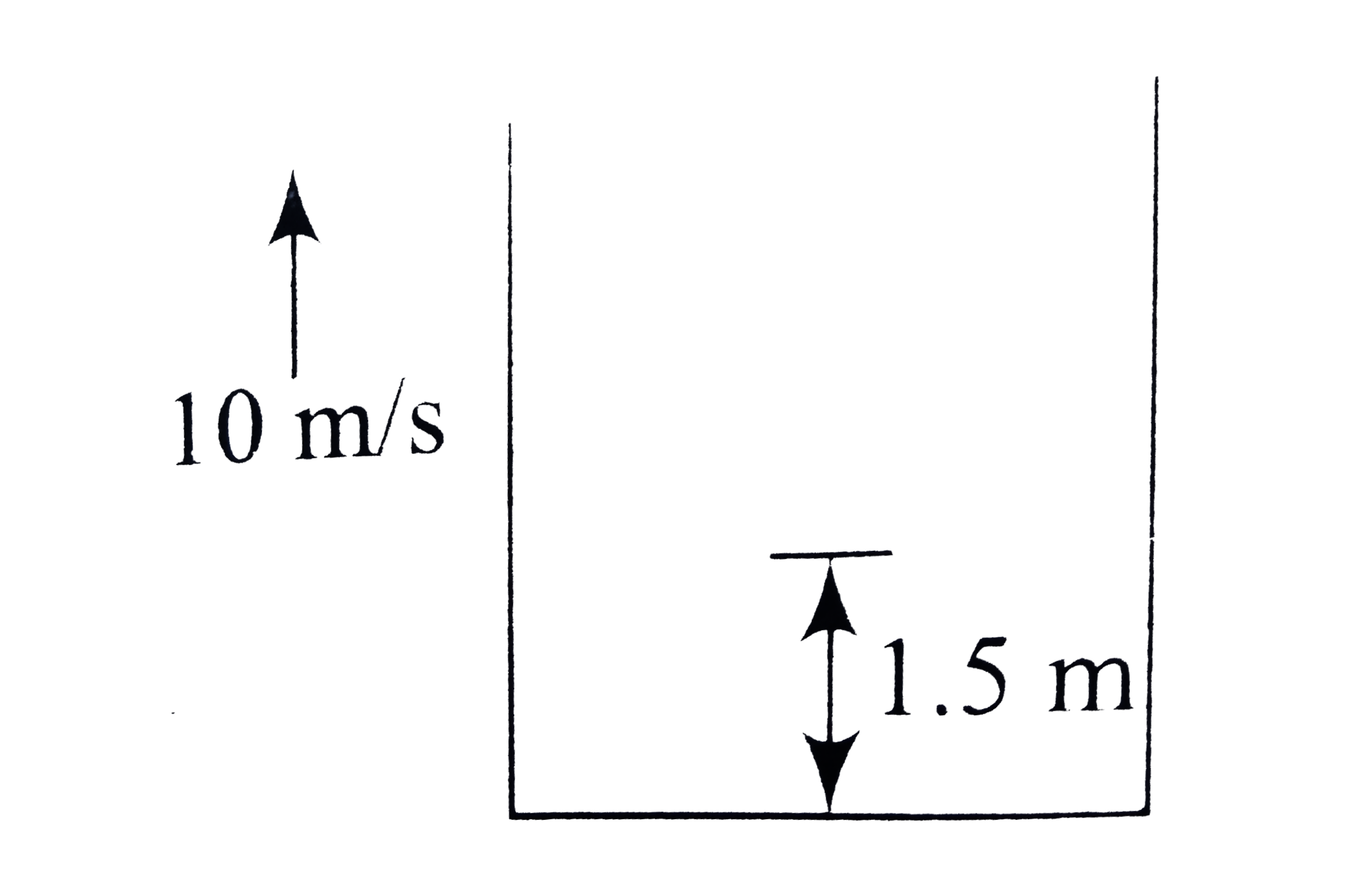
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:
View Solution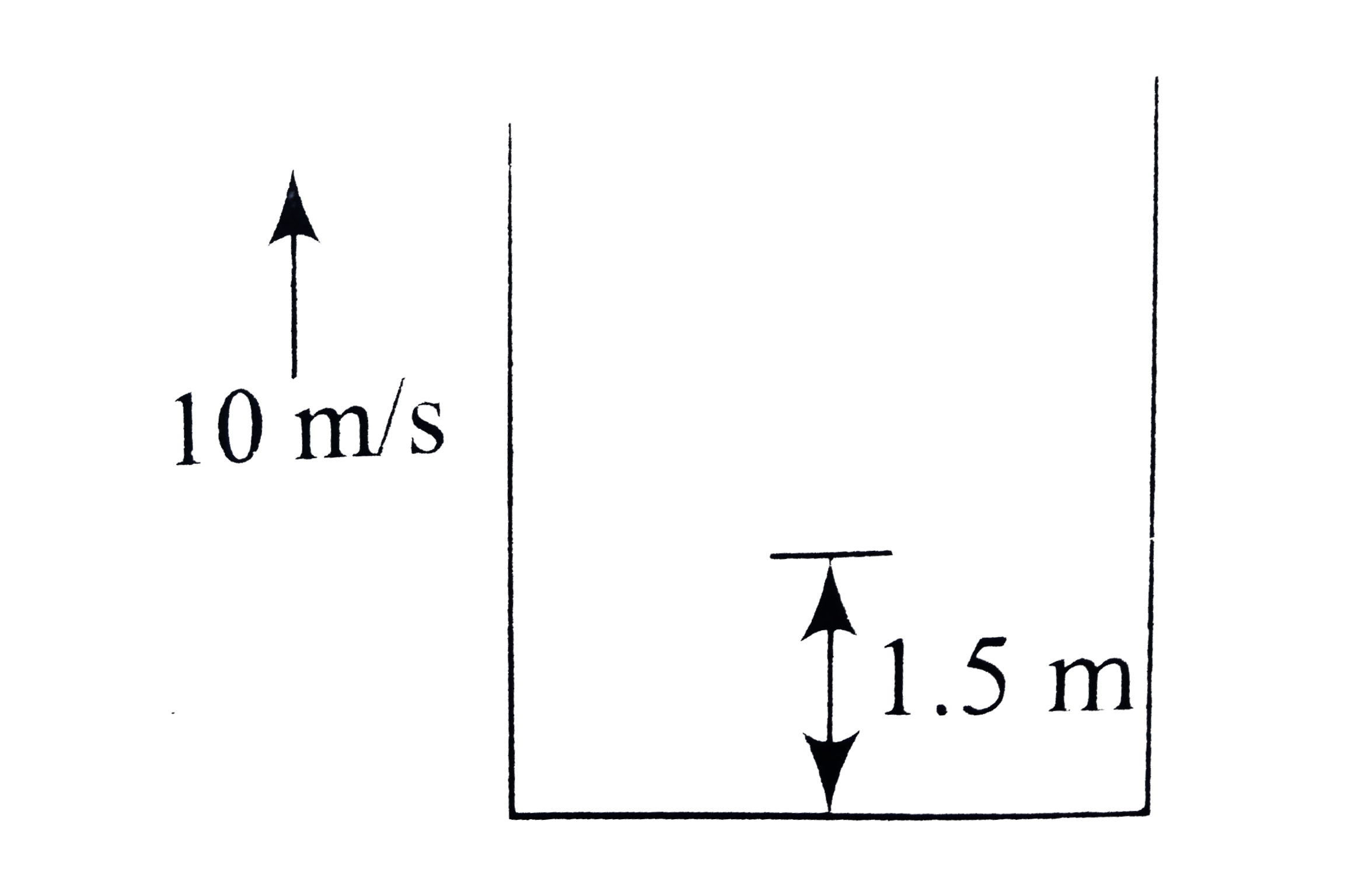
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the distance travelled by bullet during its flight:
View SolutionAn elevator, in which a man is standing, is moving upward with a constant acceleration of 2m/s2. At some instant when speed of elevator is 10m/s, the man drops a coin from a height of 1.5m. Find the time taken by the coin to reach the floor.
View Solution
