A particle is projected from ground with velocity $40 m / s$ at $60^{\circ}$ from horizontal.
(a) Find the speed when velocity of the particle makes an angle of $37^{\circ}$ from horizontal.
(b) Find the time for the above situation.
(C ) Find the vertical height and horizontal distance of the particle from the starting point in the above position. Take $g = 10 m / s^{2}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

In the figure shown,
$u_{x} = 40 {cos 60}^{\circ} = 20 m / s$
$u_{y} = 40 {sin 60}^{\circ} = 20 \sqrt{3} m / s$
$a_{x} = 0 and a_{y} = - 10 m / s^{2}$
(a) Horizontal component of velocity remains unchanged.

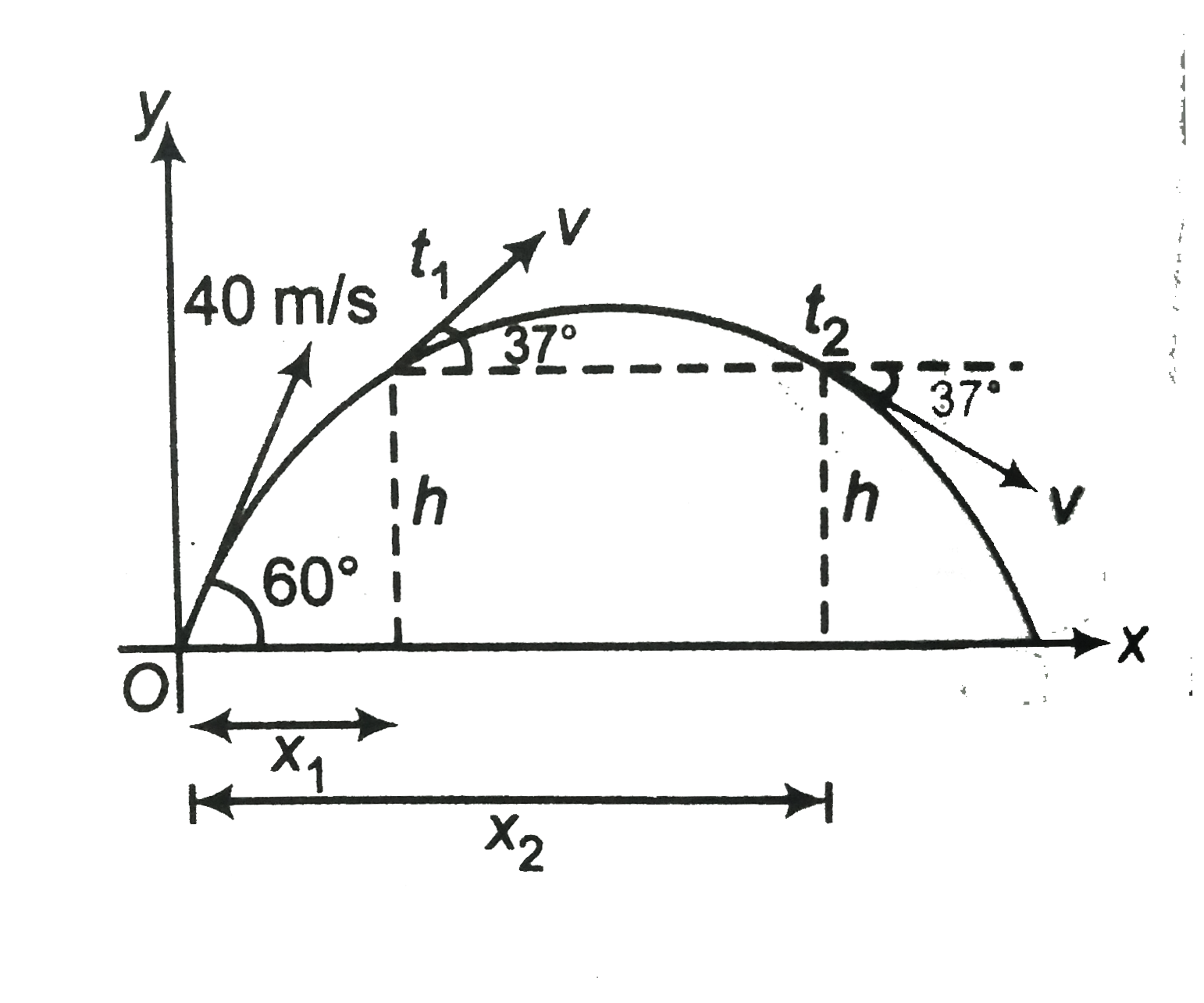
$v_{x} = u_{x}$
or $v {cos 37}^{\circ} = 20$
$\Rightarrow v (0.8) = 20$
$∴ v = 25 m / s$ .
(b) Using, $v_{y} = u_{y} + a_{y} t \Rightarrow t = \frac{v_{y} - u_{y}}{a_{y}}$
$F or t_{1}, t_{1} = \frac{v {sin 37}^{\circ} - 20 \sqrt{3}}{- 10} = \frac{(25) (0.6) - 20 \sqrt{3}}{- 10} = 1.96 s$
$F or t_{2}, t_{2} \frac{- v {sin 37}^{\circ} - 20 \sqrt{3}}{- 10} = \frac{- (25) (0.6) - 20 \sqrt{3}}{- 10} = 4.96 s$
(c) Vertical height $h = s_{y}$
Let us calculate at $t_{1}$
$∴ h = u_{y} t_{1} + \frac{1}{2} a_{y} t_{1}^{2} = (20 \sqrt{3}) (1.96) + \frac{1}{2} (- 10) {(1.96)}^{2}$
=48.7 m.
Horizontal distance
$x_{1} = u_{x} t_{1}$
= (20)(1.96) = 39.2m
Similarly, $x_{2} = u_{x} t_{2} = (20) (4.96)$
=99.2 m.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is projected with velocity 50 m/s at an angle $60^{\circ}$ with the horizontal from the ground. The time after which its velocity will make an angle $45^{\circ}$ with the horizontal is
A2.5 s
B1.83 s
C2.37 s
D3.72 m
Question 2 - Select One
A particle is projected from horizontal ground with speed $5 m s^{- 1}$ at $53^{\circ}$ with horizontal. Find time after which velocity of particle will be $45^{\circ}$ with horizontal:
A $\frac{1}{10}$ sec
B $\frac{3}{10}$ sec
C $\frac{5}{10}$ sec
D $\frac{7}{10}$ sec
Question 3 - Select One
A particle is projected from horizontal XZ plane with velocity $(u_{x} ˆ i + u_{y} ˆ i + u_{z} ˆ k)$ from origin (+ yaxis is upward). Find time when velocity of particle will be at $37^{\circ}$ with horizontal.
A $\frac{u_{y} \sqrt{u_{x}^{2} + u_{z}^{2}}}{g}$
B $\frac{3 u_{y} - 4 \sqrt{u_{x}^{2} + u_{z}^{2}}}{3 g}$
C $\frac{3 u_{y} + 4 \sqrt{u_{x}^{2} + u_{z}^{2}}}{3 g}$
D $\frac{u_{y} + \sqrt{u_{x}^{2} + u_{z}^{2}}}{3 g}$

DC PANDEY-PROJECTILE MOTION-Example Type 1

A particle is projected from ground with velocity 40 m//s at 60^@ from...
05:48

Home
Ask Doubt
Profile