Repeat the above problem, if instead of μ, we are given μs and μk,where μs=0.6 and μk=0.4.
(a) R=mg=20N
μsR=0.6×20=12N
μkR=0.4×20=8N
Upto 6ssituation is same but after 6s, a constant kinetic friction of 8N will act. At 6s, friction will suddenly change from 12N(=μsR)to8N(=μsR) and direction of friction is opposite to its motion. Therefore, at 6s it will start with an inital acceleration.
a=decreasein figuremass=12−82=2m/s2
For t≤6s
f=F=2t ...(i)
Fnet=F−f=0
a=Fnetm=0
For t≥6s
F=2t
f=μR=8N
Fnet=F−f=2t−8
a=Fnetm=2t−82=(t−4)
At t=6s,we can see that, ai=2m/s2
Further, a−t graph is a straight line of slop =1 and intercept =−4. Corresponding a−t graph is as shown in figure.

Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Miscellaneous Examples
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.1
Explore 10 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A child pushes a box that has mass m up an incline plane at an angle α above the horizontal. The coefficients of friction between the incline and the box are μs and μk. The force applied by the child is horizontal, (a )If μs is greater than some critical value, the child cannot start the box moving up the incline, no matter how hard he pushes. Calculate this critical value of μs. (b) Assume that μs is less than this critical value. What magnitude of force must the child apply to keep the box moving up the plane at constant speed.
[cotα,mg(sinα+μkcosα)cosα−μksinα]
View SolutionIf the magnetic dipole moment of an atom of diamagnetic material , paramagnetic material and ferromagnetic amterial are denote by μd,μpandμf respectively, then:
(a) μp=0andμf≠0
(b) μd=0andμp≠0
(c) μd≠0andμp=0
(d) μd≠0andμp=0
View Solution
Knowledge Check
In the above problem car got a stopping distance of 80m on cement road then μk is (g=10ms−2)
A0.2B0.25C0.3D0.35Blocks A and B in the Fig are connected by a bar of negligible weight .Mass of each block is 170kg and μA=0.2 and μB=0.4 where μA and μBare the coefficient of limiting friction between bloock and plane calculate the force developed in the bar(g=10ms−2)
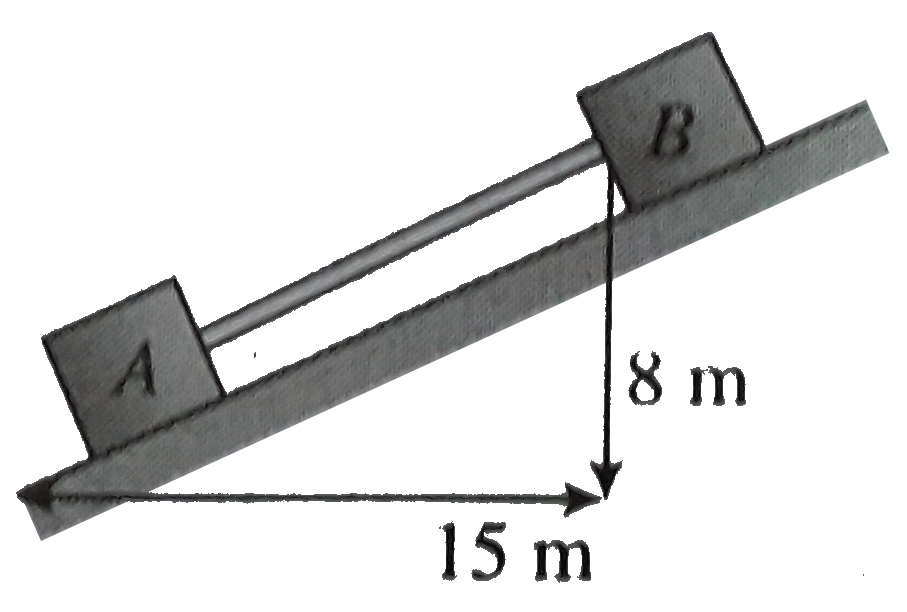 A150NB75NC200ND250N
A150NB75NC200ND250NThe dimensions of μ0 are
A[M1L−1/2T1/2]B[M1L1/2T−1/2]C[L−1T]D[M1L1T−2A−2]
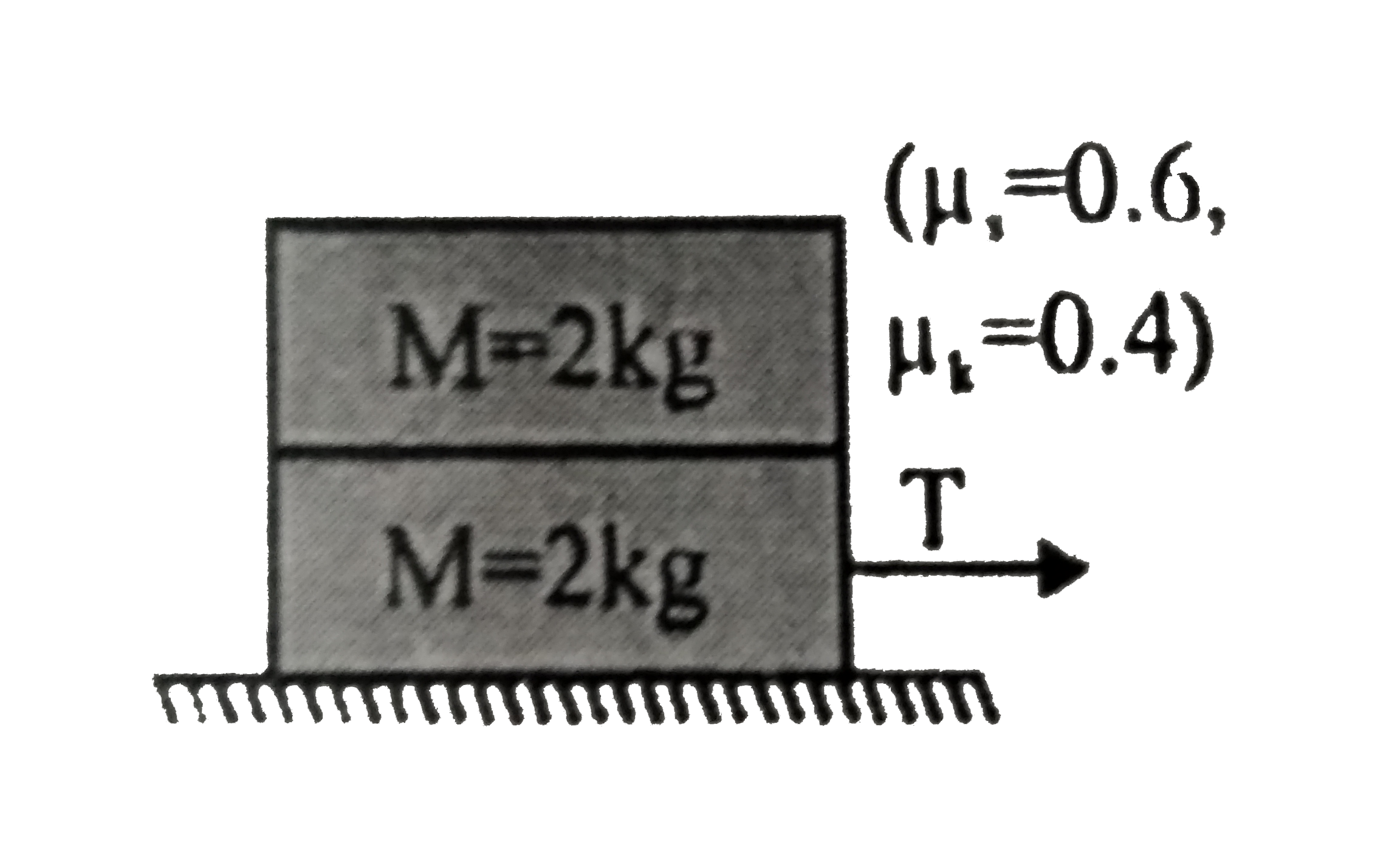
The coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are μs=0.6andμk=0.4 Find the value of tension T applied on the lower block at which the upper block begins to slip relative to lower block.
View SolutionFigure shows two blocks in contact sliding down an inclined surface of inclination 30º. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and the incline is μ2. Calculate the acceleration of the 2.0 kg block if μ1 = 0.30 and μ2 = 0.20, Take g = 10 m/s2

View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The initial shape of the wavefront of the beam is
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
The speed of light in the medium is
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
As the beam enters the medium, it will
View Solution
