If a ladder weighting 250N in placed a smooth vartical wall having coefficient of friction between it and floor 03, then what is the maximum force of fraction available at the point of contact between the ladder and the floor?
75N
50N
35N
25N
The correct Answer is:A
To solve the problem of finding the maximum force of friction available at the point of contact between the ladder and the floor, we can follow these steps:
1. Identify the Given Data:
- Weight of the ladder (W) = 250 N
- Coefficient of friction (μ) = 0.3
2. Understand the Forces Acting on the Ladder:
- The ladder is in equilibrium, meaning that the sum of the vertical forces and the sum of the horizontal forces must both be zero.
- The weight of the ladder acts downward at its center of mass.
- The normal force (N2) acts upward from the floor.
- There is no friction from the wall since it is smooth.
3. Balance the Vertical Forces:
- In the vertical direction, the normal force (N2) must balance the weight of the ladder:
N2=W=250N
4. Calculate the Maximum Force of Friction:
- The maximum force of friction (f_max) can be calculated using the formula:
fmax=μ⋅N2
- Substitute the values:
fmax=0.3⋅250N=75N
5. Conclusion:
- The maximum force of friction available at the point of contact between the ladder and the floor is:
Maximum Force of Friction=75N
Final Answer:
The maximum force of friction available at the point of contact between the ladder and the floor is 75 N.
---
- Weight of the ladder (W) = 250 N
- Coefficient of friction (μ) = 0.3
- The ladder is in equilibrium, meaning that the sum of the vertical forces and the sum of the horizontal forces must both be zero.
- The weight of the ladder acts downward at its center of mass.
- The normal force (N2) acts upward from the floor.
- There is no friction from the wall since it is smooth.
- In the vertical direction, the normal force (N2) must balance the weight of the ladder:
N2=W=250N
- The maximum force of friction (f_max) can be calculated using the formula:
fmax=μ⋅N2
- Substitute the values:
fmax=0.3⋅250N=75N
- The maximum force of friction available at the point of contact between the ladder and the floor is:
Maximum Force of Friction=75N
The maximum force of friction available at the point of contact between the ladder and the floor is 75 N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.5
2 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionThe friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View Solution
Knowledge Check
If a lodder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3 then what is the maximum force of friction available at the point of contact between the lodder and the floor?
A75NB50NC35ND25NIf a lodder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3 then what is the maximum force of friction available at the point of contact between the lodder and the floor?
A75NB50NC35ND25NA ladder wighing 300 N is placed against a smooth vertical wall having a coefficient of friction between it and the floor of 0.2. What is the maximum force of friction available at the point of contact between the ladder and the floor?
A40 NB50 NC60 ND70 N
A block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
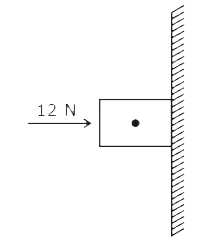
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
View SolutionThe friction coefficient between the plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then :

View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :

View Solution
