A body is displaced from prigin to (1m,1m) by force
F=(2yˆi+3x2ˆj) along two paths
(a) x=y (b) y=x2
Find the work done along both paths.
F=(2yˆi+3x2ˆj)
dr=(dxˆi+dyˆj)
F.dr=(2ydx+3x2dy)
We cannot integrate F.dr or (2ydx+3x2dy) as such to find the work done. But along the given paths we can change this expression.
(a) Along the path x=y
(2ydx+3x2dy)=(2xdx+3y2dy)
W1=∫1m,1m,0,0F.dr=∫1m,1m0,0(2xdx+3y2dy)
=[x2+y3]1m,1m0,0
=(1)2+(1)3=2J
(b) Along the path y=x2
(2ydx+3x2dy)=(2x2dx+3ydy)
∴W=(2)=∫1m,1m0,0F.df=∫(2x2dx+3ydy)
=[23x3+32y2]1m,1m0,0
=136J
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE21videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example6videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A body is desplaced from origin to (2m,4m) under the following two forces:
(a) F=(2ˆi+6ˆj)N, a constant force
(b) F(2xˆi+3y2ˆj)N
Find word done by the given forces in both cases.View SolutionAn object is displaced from point A(2m,3m,4m) to a point B(1m,2m,3m) under a constant force F=(2ˆi+3ˆj+4ˆk)N. Find the work done by this force in this process.
View Solution
Knowledge Check
- Question 1 - Select One
A body is displaced from (0,0) to (1m,1m) along the path x=y by a force F=(x2ˆj+yˆi)N. The work done by this force will be
A43JB56JC32JD75J - Question 2 - Select One
A particle is moved from (0,0)to (a,a) under a force ¯¯¯F=(3ˆi+4ˆj) and path 2isOQP.Let W1andW2 be the work by done this force in these to paths .Then .
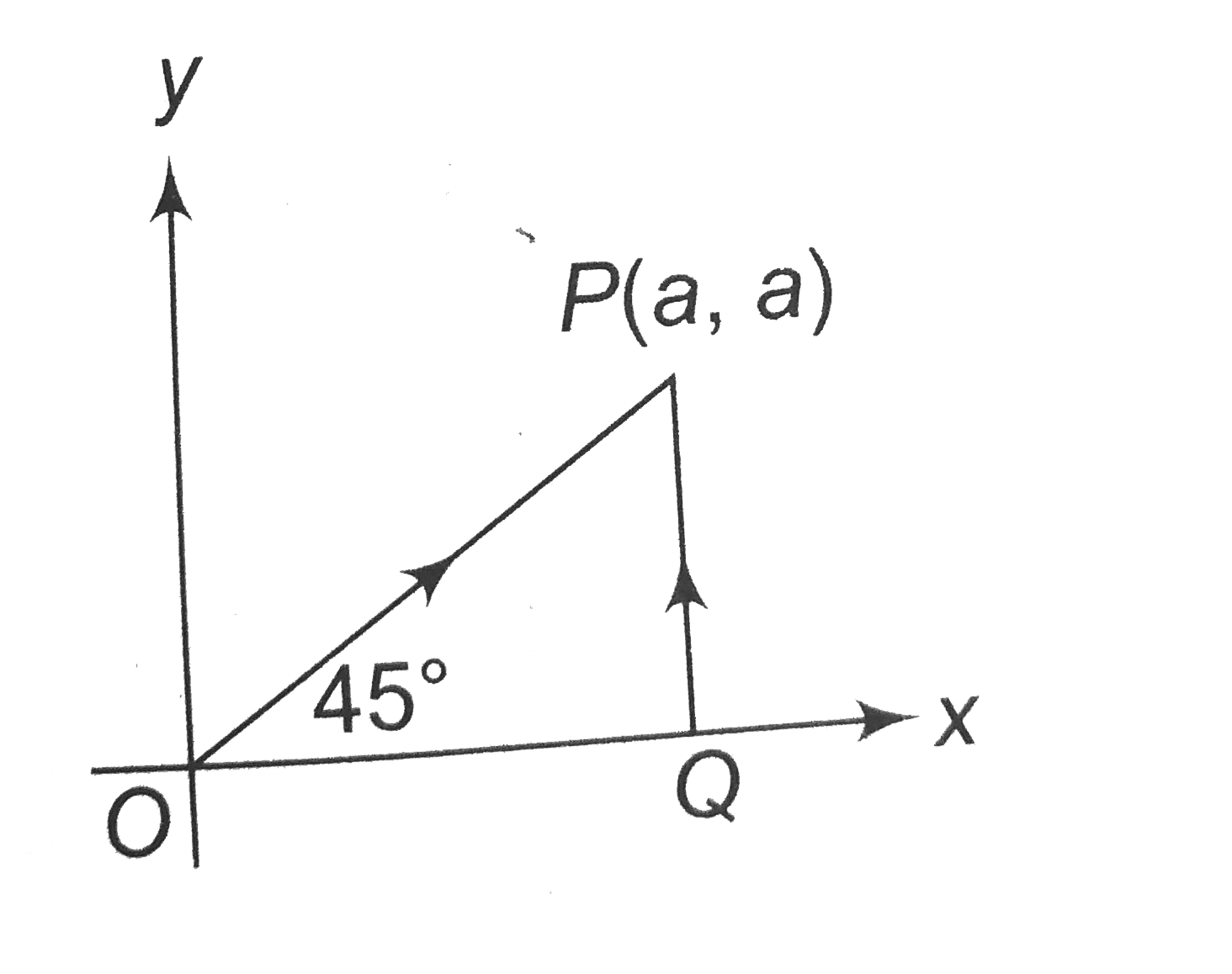 AW1=W2BW1=2W2CW2=2W1DW2=4W1
AW1=W2BW1=2W2CW2=2W1DW2=4W1 - Question 3 - Select One
A particle is movbed from (0,0)→(a,a) under a force F=(x2ˆi+y3ˆj) from two paths. Path 1 si OP and Path 2 is OQP. Let W1 and W2 be the work done by this force in these two paths. Then
 AW1=W2BW1=2W2CW2=2W2DW2=4W1
AW1=W2BW1=2W2CW2=2W2DW2=4W1
An object is displaced from a point A(0, 0, 0) to B(1m, 1m , 1m) under a force →F=(yˆi+xˆj)N. Find the work done by this force in this process.
View SolutionAn object is displaced from positin vector r1=(2ˆi+3ˆj) m to r2=(4ˆi+6ˆj) m under a forc F=(3x2ˆi+2yˆj)N Find the work done by this force.
View SolutionA block is displaced from (1m,4m,6m) to (2ˆi+3ˆj−4ˆk)m under a constant force F=(6ˆi−2ˆj+ˆk)N. Find the work done by this force.
View SolutionA body displaced from (1,1) to (2,2) along the line y=x under the force →F=xˆj+yˆi then find the work done by this force for above displacement. (all units are in S.I.)
View SolutionDue to a force of (6ˆi+2ˆj)N the displacement of a body is (3ˆi−ˆj)m, then the work done is
View Solution

