A particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
where , k=constant
Derive an expression for the force an the particle.
Force acting an the particle in x-direction is given by
Similarly, and
Force acting an the particle is
,
where r =position vector of the particle
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.120videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.220videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
Similar Questions
A particle slides on frictionless x - y plane. It is acted on by a conservative force described by the potential - energy function U(x,y)=12k(x2+y2). Derive an expression for the force acting on the particle.
View SolutionIf the potential energy function of a particle is given by U=−(x2+y2+z2)J, whre x,y and z are in meters. Find the force acting on the particle at point A(1m,3m,5m).
View Solution
Knowledge Check
- Question 1 - Select One
A particle in a certain conservative force field has a potential energy given by U=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk - Question 2 - Select One
As a particle moves along the x−axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
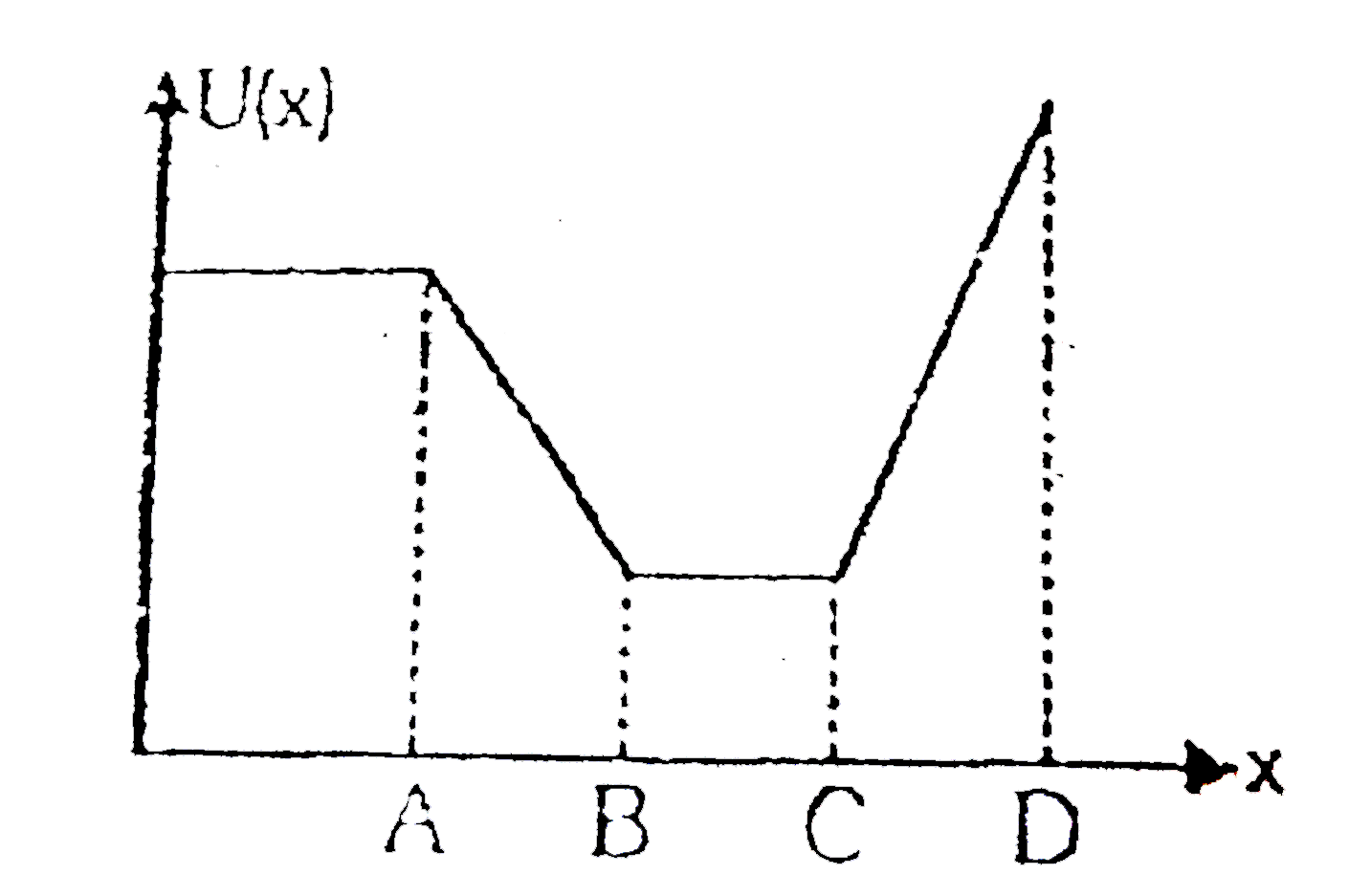 AAB, BC, CDBAB, CD, BCCBC, CD, ABDBC, AB, CD
AAB, BC, CDBAB, CD, BCCBC, CD, ABDBC, AB, CD - Question 3 - Select One
A particle in a certain conservative force field has a potential energy given by V=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk
A particle is moving in a potential region defined by U=K(x2+y2+z2). Calculate the force acting on the particle.
View SolutionA conservative force F(x) act on a 1kg particle. The potential energy U(x)=(x−4)2 , At x=5 ,particle has kinetic energy of 24J .The greatest value of x to which particle can move is
View SolutionFigure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)
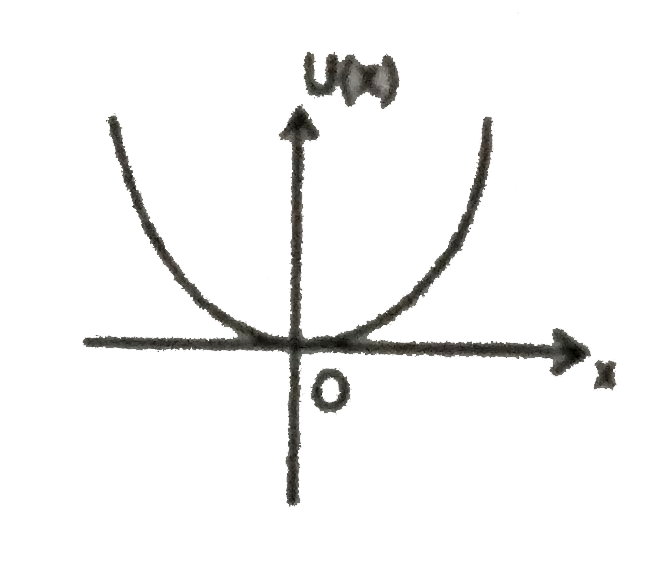 View Solution
View SolutionA particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View SolutionA particle of mass m is moving in circular path of constant radius r such that centripetal acceleration is varying with time t as k2rt2 where k is a constant the power deleivered to the particle by the force acting on its is
View Solution

