If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficient so that a scooter going at 18km/h does not skid?
The correct Answer is:B
To solve the problem of finding the minimum friction coefficient required for a scooter to navigate a horizontal turn without skidding, we can follow these steps:
1. Convert the Speed from km/h to m/s:
The speed of the scooter is given as 18 km/h. To convert this to meters per second (m/s), we use the conversion factor:
1 km/h=13.6 m/s
Therefore,
v=18 km/h×13.6=5 m/s
2. Identify the Radius of the Turn:
The radius of the turn is given as r=10 meters.
3. Use the Formula for Circular Motion:
The formula relating the velocity, friction coefficient (μ), radius (r), and gravitational acceleration (g) is:
v=√μ⋅r⋅g
Here, g (acceleration due to gravity) is approximately 10m/s2.
4. Rearrange the Formula to Solve for μ:
Squaring both sides of the equation gives:
v2=μ⋅r⋅g
Rearranging for μ gives:
μ=v2r⋅g
5. Substitute the Known Values:
Now, substituting the values we have:
- v=5m/s
- r=10m
- g=10m/s2
We get:
μ=5210⋅10
μ=25100=0.25
6. Conclusion:
The minimum friction coefficient required for the scooter to navigate the turn without skidding is μ=0.25.
The speed of the scooter is given as 18 km/h. To convert this to meters per second (m/s), we use the conversion factor:
1 km/h=13.6 m/s
Therefore,
v=18 km/h×13.6=5 m/s
The radius of the turn is given as r=10 meters.
The formula relating the velocity, friction coefficient (μ), radius (r), and gravitational acceleration (g) is:
v=√μ⋅r⋅g
Here, g (acceleration due to gravity) is approximately 10m/s2.
Squaring both sides of the equation gives:
v2=μ⋅r⋅g
Rearranging for μ gives:
μ=v2r⋅g
Now, substituting the values we have:
- v=5m/s
- r=10m
- g=10m/s2
μ=5210⋅10
μ=25100=0.25
The minimum friction coefficient required for the scooter to navigate the turn without skidding is μ=0.25.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.34videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason28videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.17videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
Block M slides down on frictionless incline as shown. The minimum friction coefficient so that m does not slide with respect to M would be :
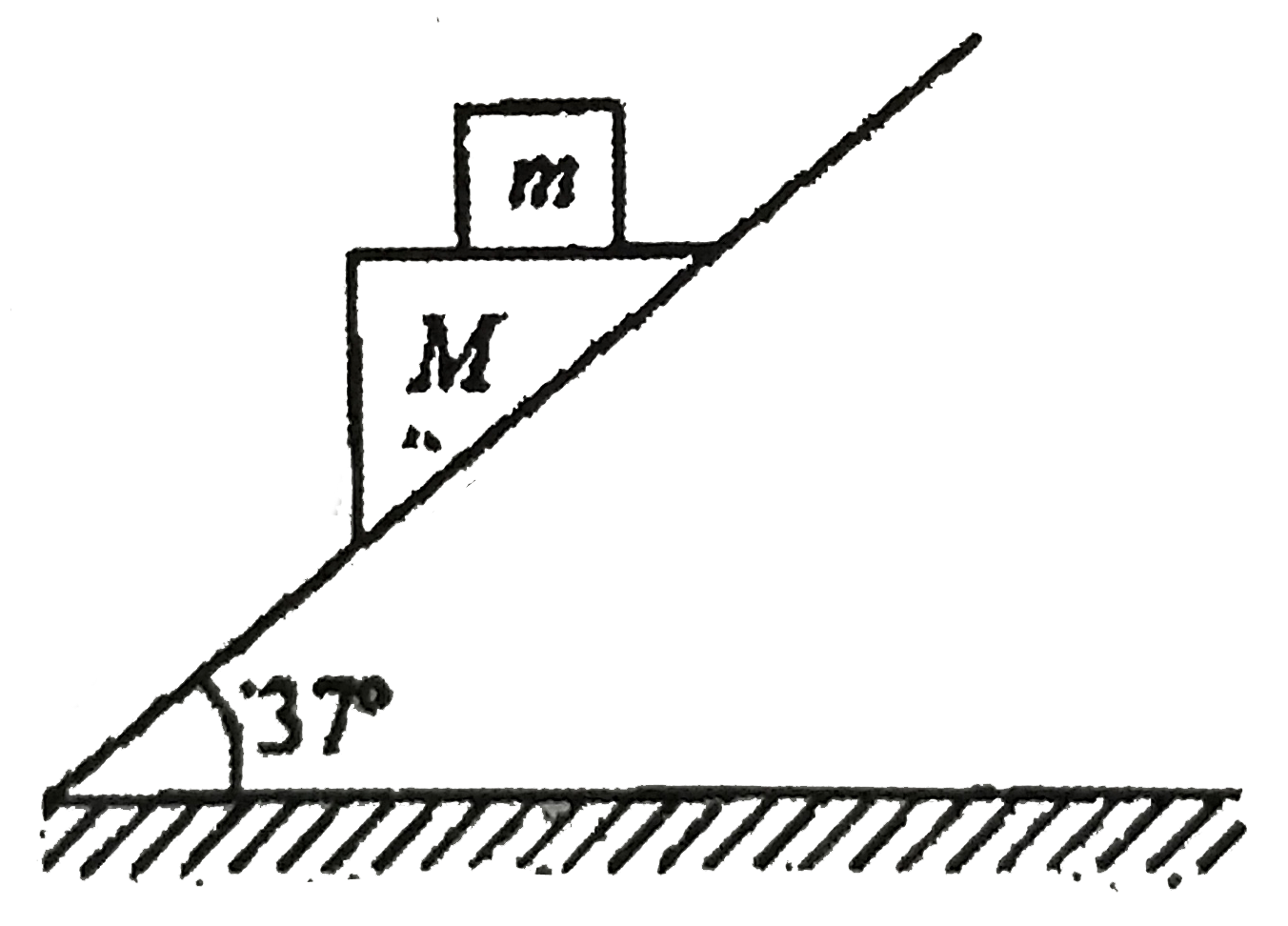 A14B12C34DNone of these
A14B12C34DNone of these - Question 2 - Select One
A cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 . AinfinitesimalBmg/4Cmg/2Dmg(1−μ)
. AinfinitesimalBmg/4Cmg/2Dmg(1−μ) - Question 3 - Select One
A sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
A2/5tanθB2/7tanθC5/7tanθDtanθ
A solid sphere of mass m rolls without slipping on an inclined plane of inclination 0. what should be the minimum coefficient of static friction to support pure rolling?
View SolutionA car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionIn the previous problem , if the horizontal surface is rough with friction coefficient 0.5 and collision is elastic , head - on , the distance travelled by the block on the rough surface
View Solution

