In the previous problem, suppose m2=2.0kgandm3=3.0kg. What should be the mass m so that it remains at rest?
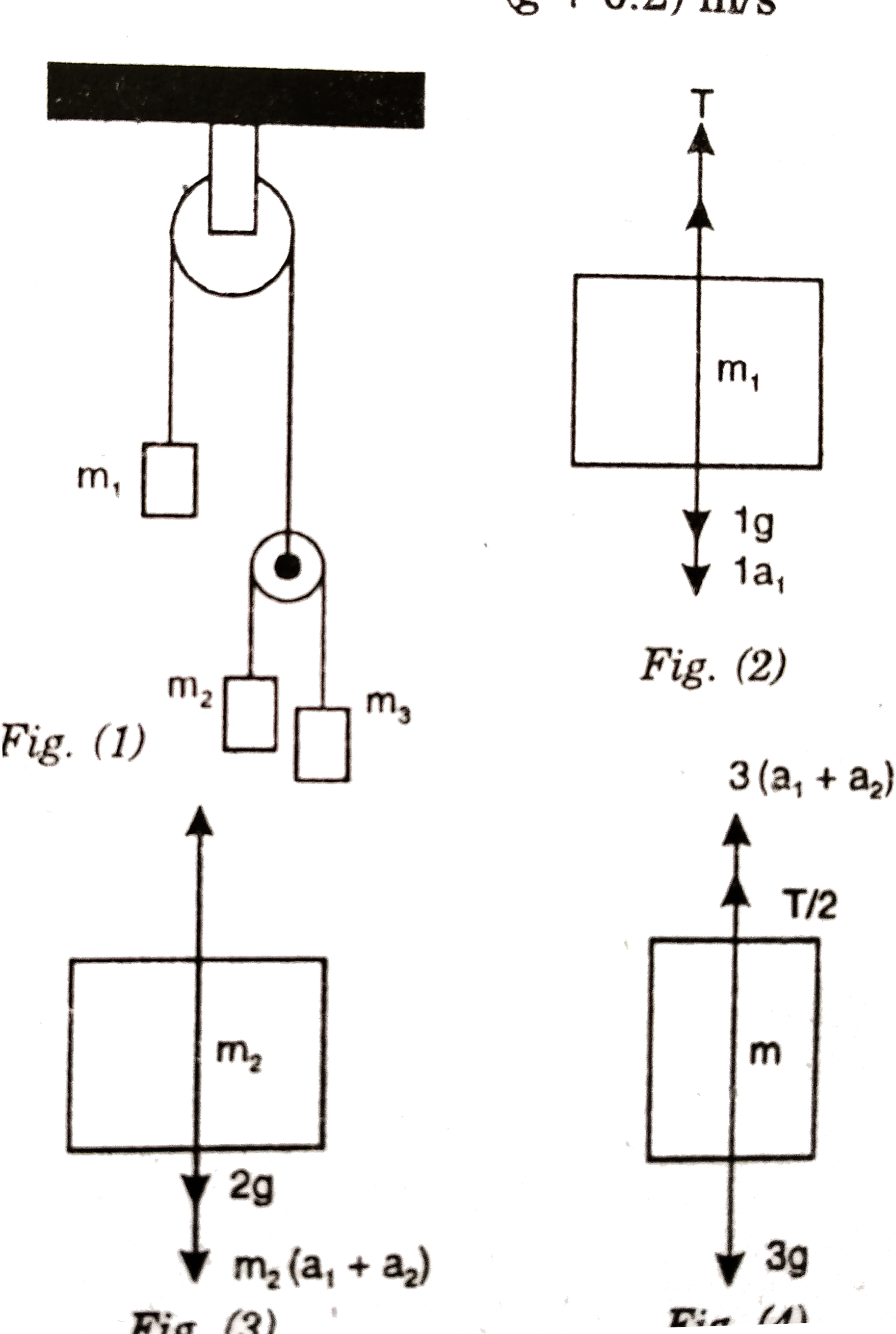
Let the block m1 moves upward with accelerastion a1 and the two block m2andm3 have relative cceleration a2 due to the diffference of weight between them,
So, the actual acceleratin of the blocks m1,m2andm3 will be a1(a1−a2)and(a1+a2) as shown
From ure 2, T−1g−1a2=0....i.
From ure 3, <br> T/2 -2 g-2(a_1-a_2)=0........ii.
From ure 4,
T2−3g−3(a1+a2)=0 ........iii.
From equations I. and ii. elimiN/Ating T, we get,
1g+1a2=4g+4(a1+a2)
→5a2−4a1=3g ...........iv.
From equations ii and iii we get
2g+2(a1−a2)=3−3(a1−a2)
→5a1+a2=g .........v.
Solving equations iv and v we get,
a1=2g29
anda2=g−5a1
=g−10g29=19g29
So, a1−a2=2g17g/29
and a1+a2=2g29+19g29=21g29
So, acceleratiion of m1,m2andm3 are (19g)/29 (up) , (17g)/29(down)and(21g)/29 (down), respectively.
Again, from u=0,S=20cm=0.2cmand<br> a_2= (19g)/29 [g=10 m/s^2]<br>∴S=ut+12at2
→0.2=12×1929>2
→t=0.25sec .
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBook:HC VERMAChapter:NEWTON'S LAWS OF MOTIONExercise:Objective 2
Explore 9 Videos
- LAWS OF THERMODYNAMICSBook:HC VERMAChapter:LAWS OF THERMODYNAMICSExercise:Short Answer
Explore 15 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMAChapter:PHYSICS AND MATHEMATICSExercise:Exercises
Explore 34 Videos
Similar Questions
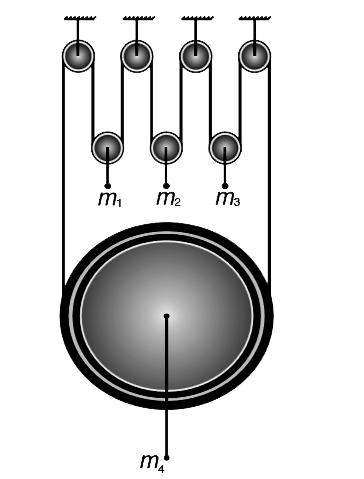
In the system shown in fig., all pulleys are mass less and the string is inextensible and light.
(a) After the system is released, find the acceleration of mass m1
(b) If m1=1kg,m2=2kgandm3=3kg then what must be value of mass m4 so that it accelerates downwards?
View SolutionA point mass m is located at (0,a). Where should the 2m mass be kept, so that centre of mass lies at origin
View Solution
Knowledge Check
Two blocks M and m are arranged as shown in the diagram The coefficient of friction between the block is μ1=0.25 and between the ground and M is μ2=13 If M=8kg then find the value of m so that the system will remain at rest
 A4/3kgB8/9kgC1kgD8/5kg
A4/3kgB8/9kgC1kgD8/5kg
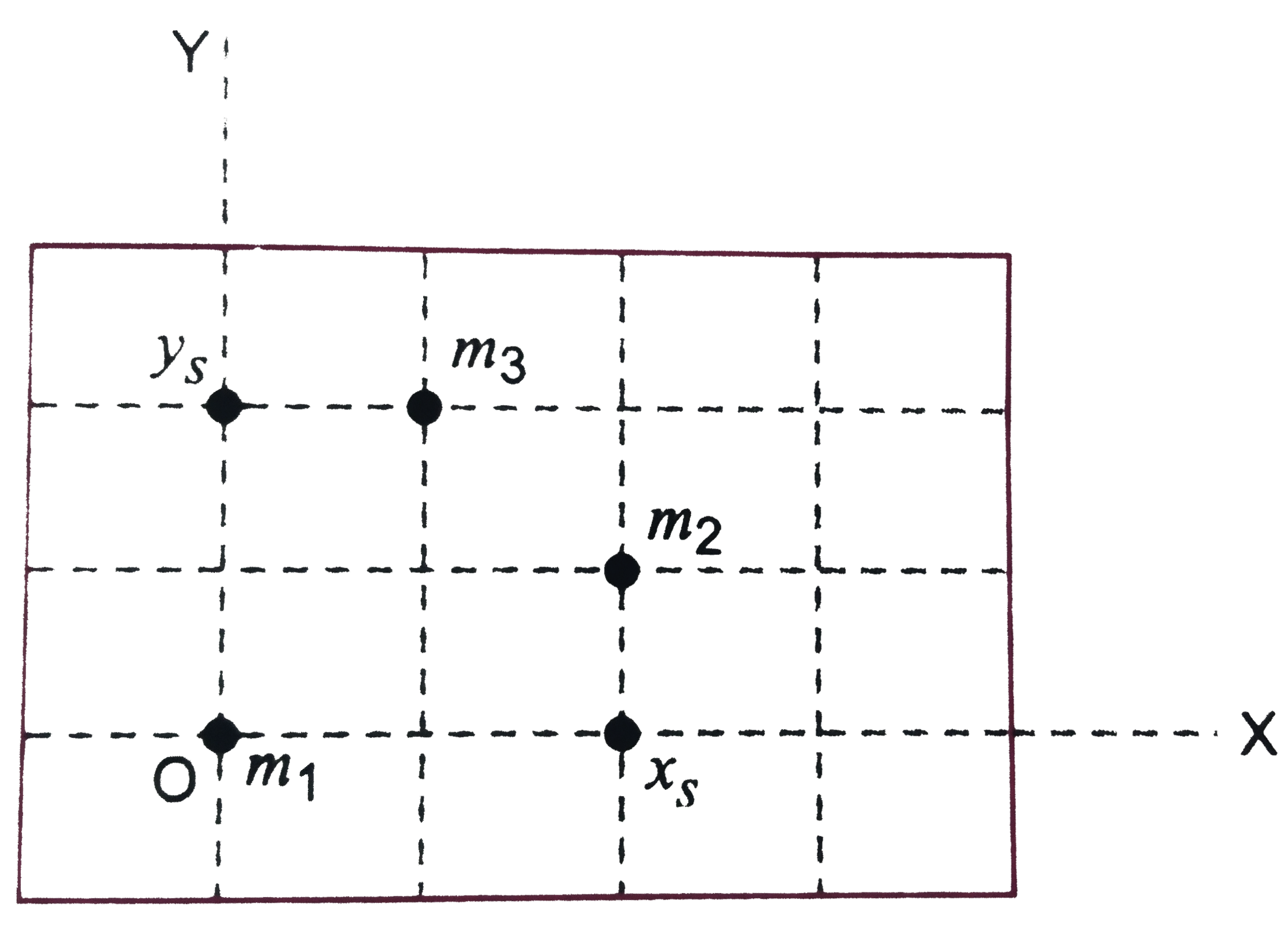
Fig. shown a three particle system with masses m1=3.0kg,m2=4.0kg and m3=8.0kg. The scales on the axes are set by xs=2.0m and ys=2.0m. What are the co-ordinates of centre if mass ? If m3 is gradually increased, does the centre of mass of the system shift towards or away from that particle or does it remain stationary ?
View SolutionSuppose the smaller pulley of the previous problem has its radius 5.0 cm and moment of inertia 0.10 kg-m^2. Find the tension in the part of the string joiningk the pulleys.
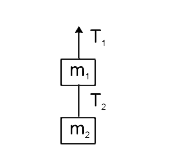
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
the blocks are at rest
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
they accelerate downward at 2m/s2
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
if maximum allowable tension is 10 N. What is maximum possible upward acceleration ?
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
they move upward at 5 m/s
View SolutionTwo blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.
View Solution