Assertion: A particle of mass m takes uniform horizontal circular motion inside a smooth funnel as shown. Normal reaction in this case is not mgcosθ .
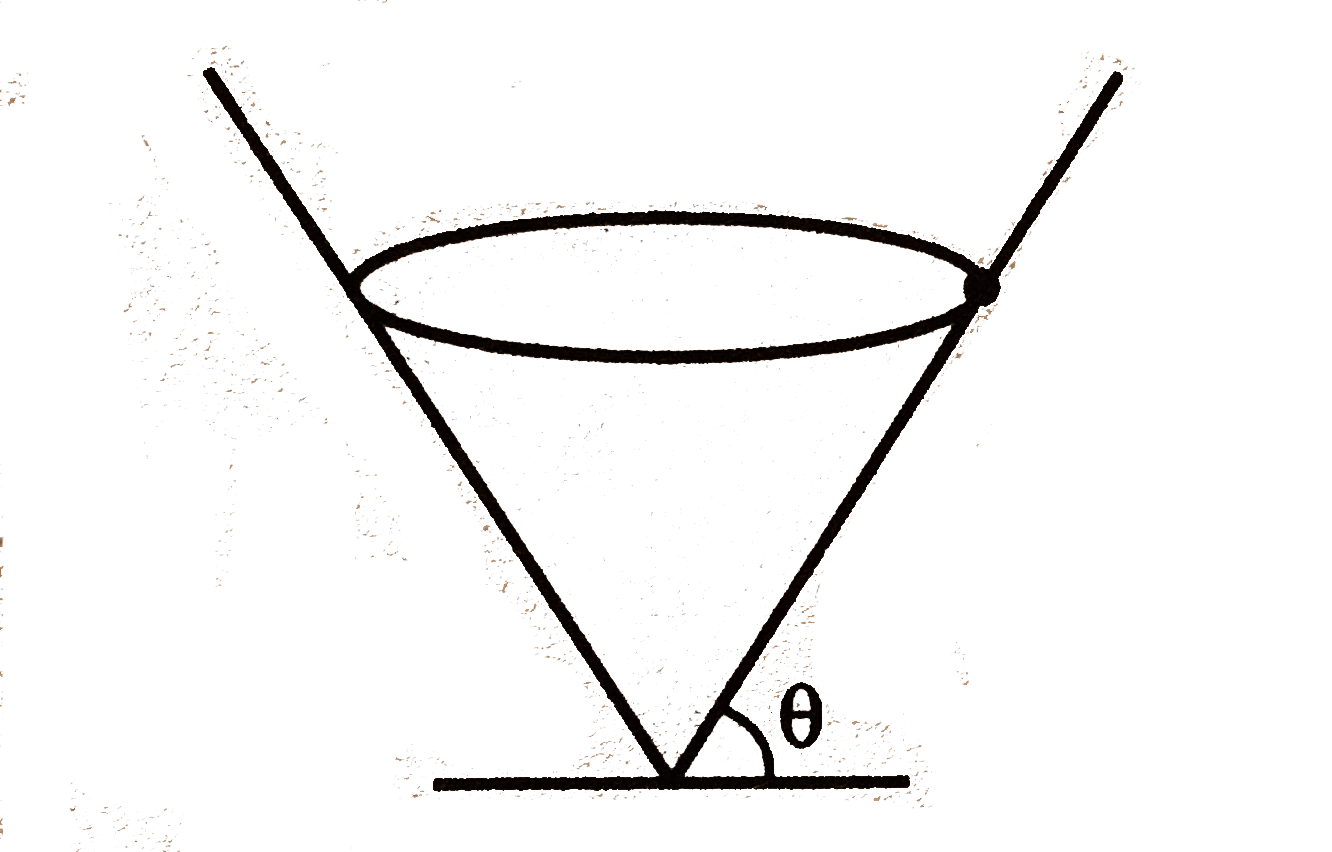
Reason: Acceleration of particle is not along the surface of funnel.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, true but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A
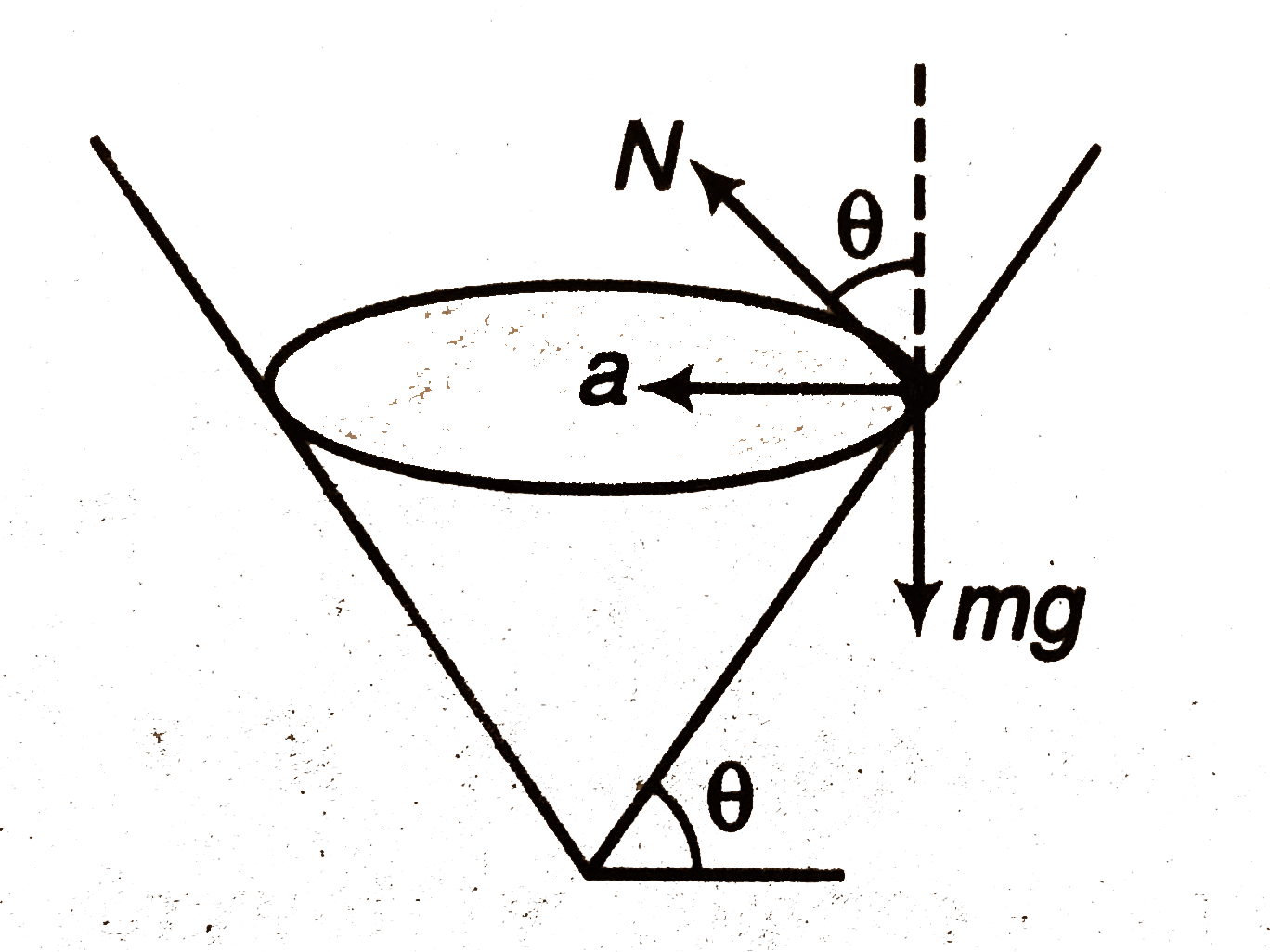
Ncosθ=mg
⇒N=mgsecθ
and Nsinθ=mv2R
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective14videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective13videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.34videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
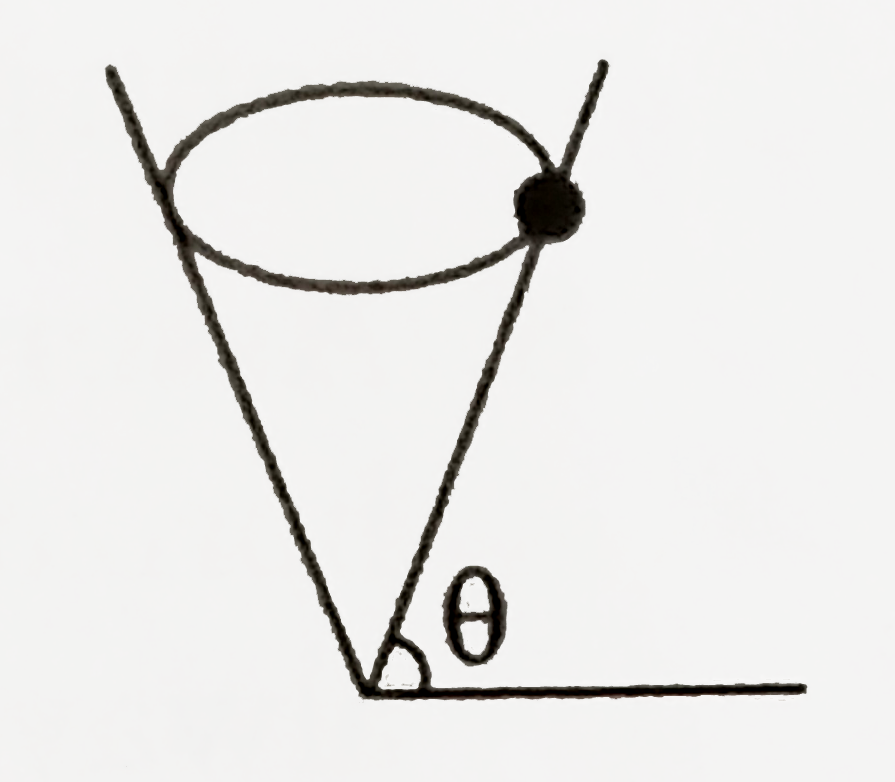
Assertion A small block of mass m is rotating in a circle inside a smooth cone as shown in figure. In this case the normal reaction,
N≠mg cosθ
Reason In this case, acceleraion of the block is not along the surface of cone. It is horizontal.
 AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.
AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true. - Question 2 - Select One
For a particle performing a uniform circular motion the acceleration is
Aconstant in directionBconstant in magnitude but not in directionCconstant in magnitude and directionDconstant neither in magnitude nor in direction. - Question 3 - Select One
For a particle in a non-uniform accelerated circular motion
AVelocity is radial and acceleration is transverse onlyBVelocity is transverse and acceleration is radial onlyCVelocity is radial and acceleration has both radial and transverse componentsDVelocity is transverse and acceleration has both radial and transverse components
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulu) as shown in the figure. If speed of the particle is constant then,
 View Solution
View SolutionIn a non uniform circular motion, the acceleration on the particle is
View SolutionThe average acceleration vector for a particle having a uniform circular motion is
View SolutionThe angular acceleration of a particle moving along a circular path with uniform speed is
View SolutionA particle of mass m oscillates along the horizontal diameter AB inside a smooth spherical shell of radius R. At any instant K.E. of the partical is K. Then force applied by particle on the shell at this instant is:
 View Solution
View Solution


