A particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.

Angular momentum of particle about point of suspension does not remains constant.
Angular momentum of particle about centre of circle remains constant.
Average force during half rotation is 2mgtanthethaπ
Average torque about axis OC during half rotation is zero
The correct Answer is:A, B, C, D

τav×Δt=L2−L1=ΔL
→L=−Lcosθˆi+Lsinθˆj,→L2=Lcosθˆi+Lsinθˆj
→L2−→L1=(2Lcosθˆi)
magnitude is same but direction of angular momentum is continuously changing So →L is not constant (B) about centre is constant (c)Tcosθ=mg......(1)
Tsinθ=mω2lsinθ..........(2)
mω2lcosθ=mg
ω2=glcosθ,ω=√glcosθ
V=ω(lsinθ)=√glcosθsinθ
Fav×Δt=ΔP=P2−P1
mV=msinθ√glcosθ
Fav=P2−P1Δt=(2msinθ)√glcosθπ/ω
Fav=2msinθπ√glcosθ×√glcosθ⇒Fav=2mgtanθπ
L will be constant about line OC as shown in diagram

Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective107videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A particle is projected from point A perpendicular to inclined plane with a velocity 50m/s as shown in the figure. Particle strikes a vertical plane perpendicularly at point B. Time taken by particle in going from point A to point B is
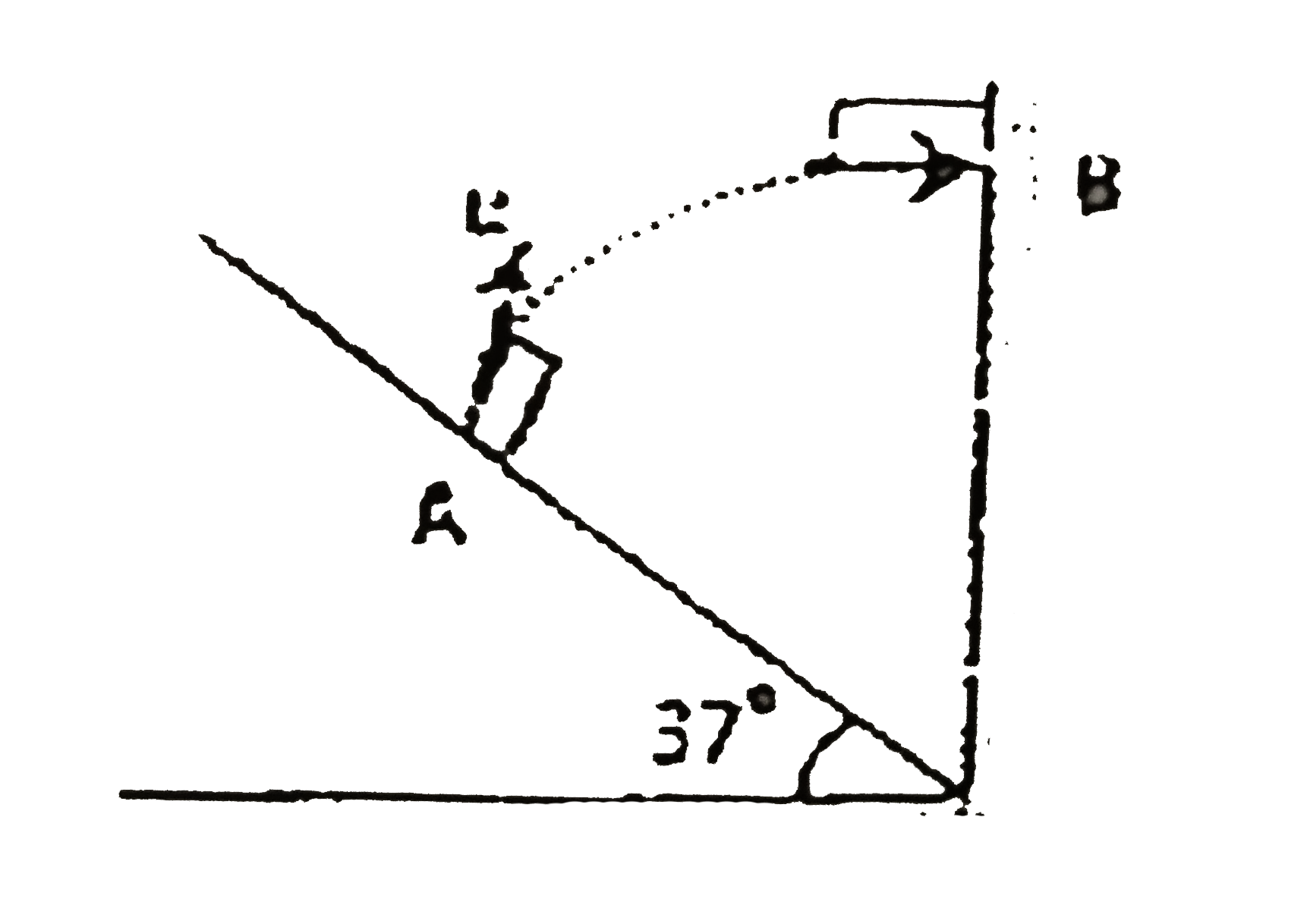 View Solution
View SolutionImportant Questions|Circular Motion In Horizontal Plane|Circulars turning On Road
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulu) as shown in the figure. If speed of the particle is constant then,
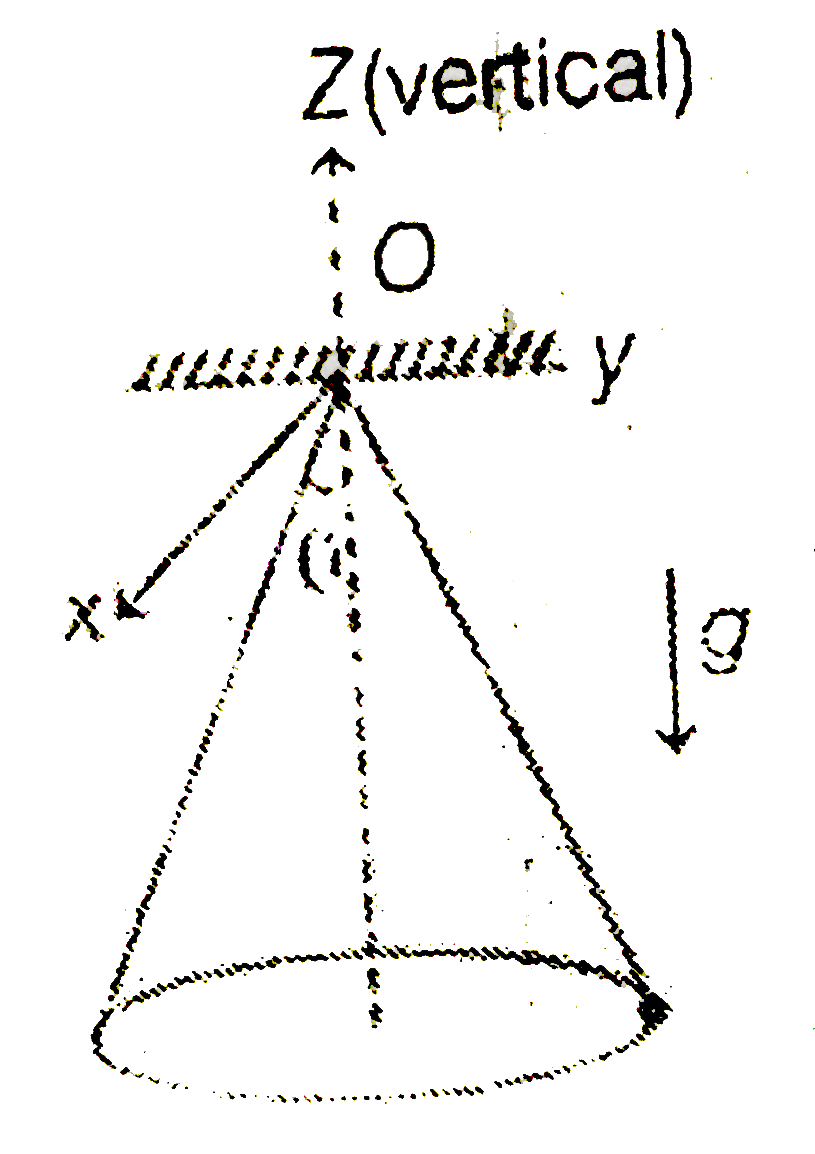 Athe angular momentum of the particle about O is changingBmagnitude of angular momentum about O remains constantCz component of the angular momentum remains conservedDz component of torque is always zero.
Athe angular momentum of the particle about O is changingBmagnitude of angular momentum about O remains constantCz component of the angular momentum remains conservedDz component of torque is always zero. - Question 2 - Select One
A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
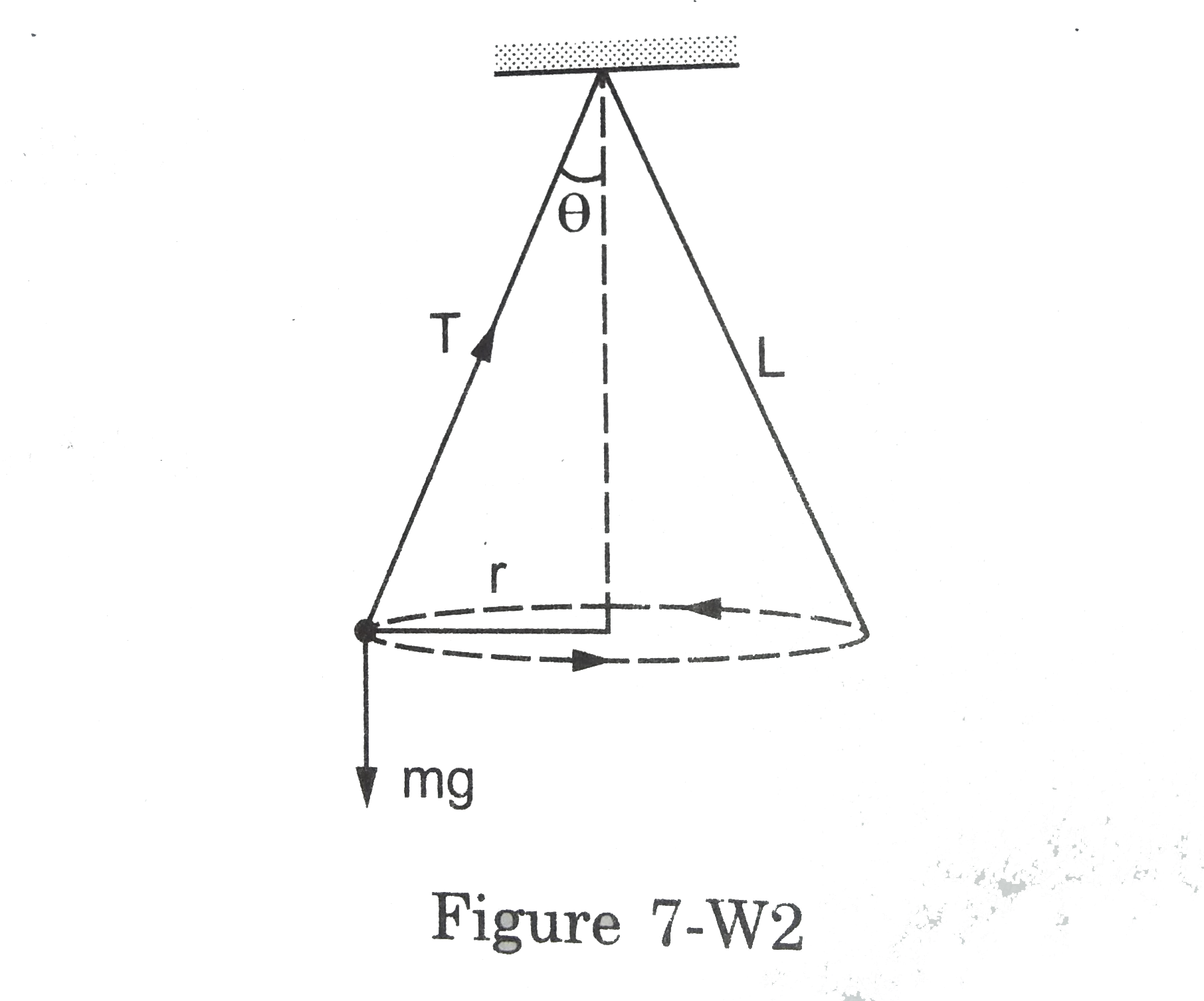
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14 - Question 3 - Select One
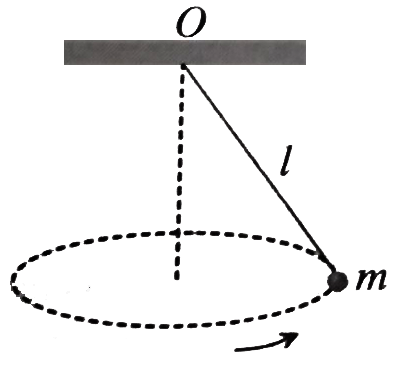
A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass areA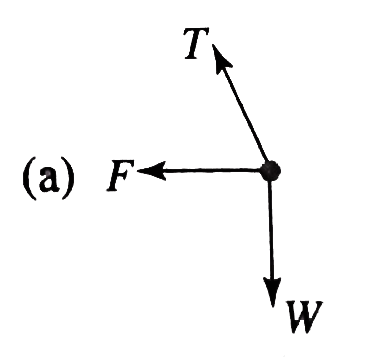 B
B C
C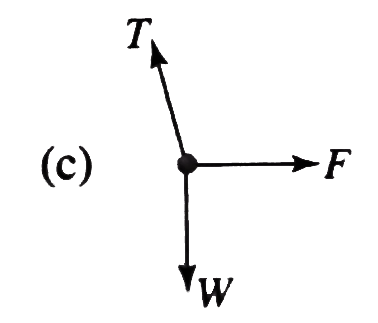 D
D
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :
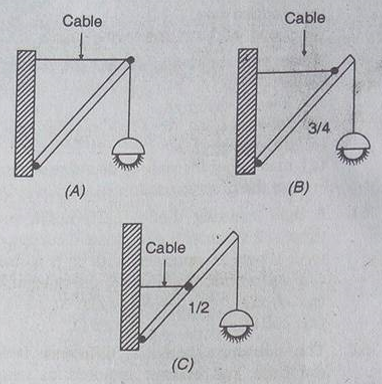 View Solution
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :
 View Solution
View SolutionIf asteel light of mass M is suspended from for end of a uniform rod of lkength L in diffrence possible patents as shown in figure
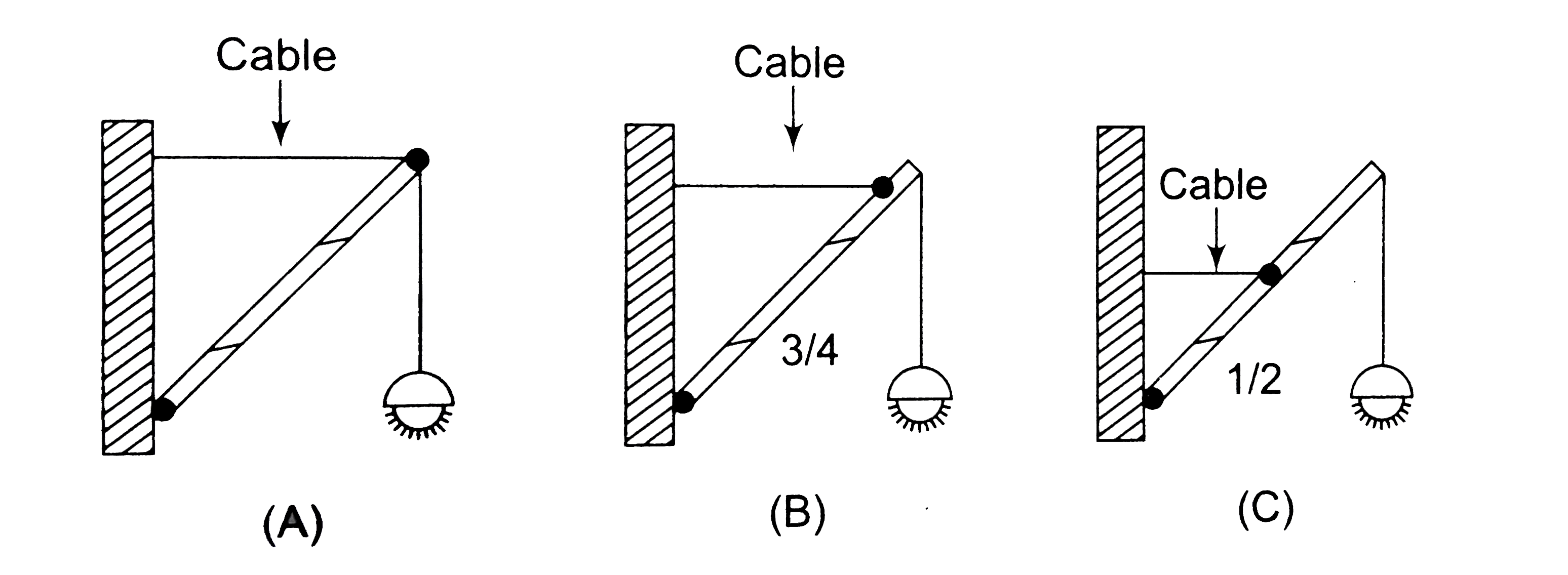 View Solution
View Solution

