A vertical frictionless semicircular track of radius 1m fixed on the edge og a movable trolley (figure). Initially, the system is rest and a mass m is kept at the top of the track. The trolly starts moving to the right with a uniform horizontal acceleration a=2g/9 . The mass slides down the track, eventually losing contact with it and dropping to the floor 1.3m below the trolly. This 1.3m is from the point where mass loses contact. (g=10m/s2)
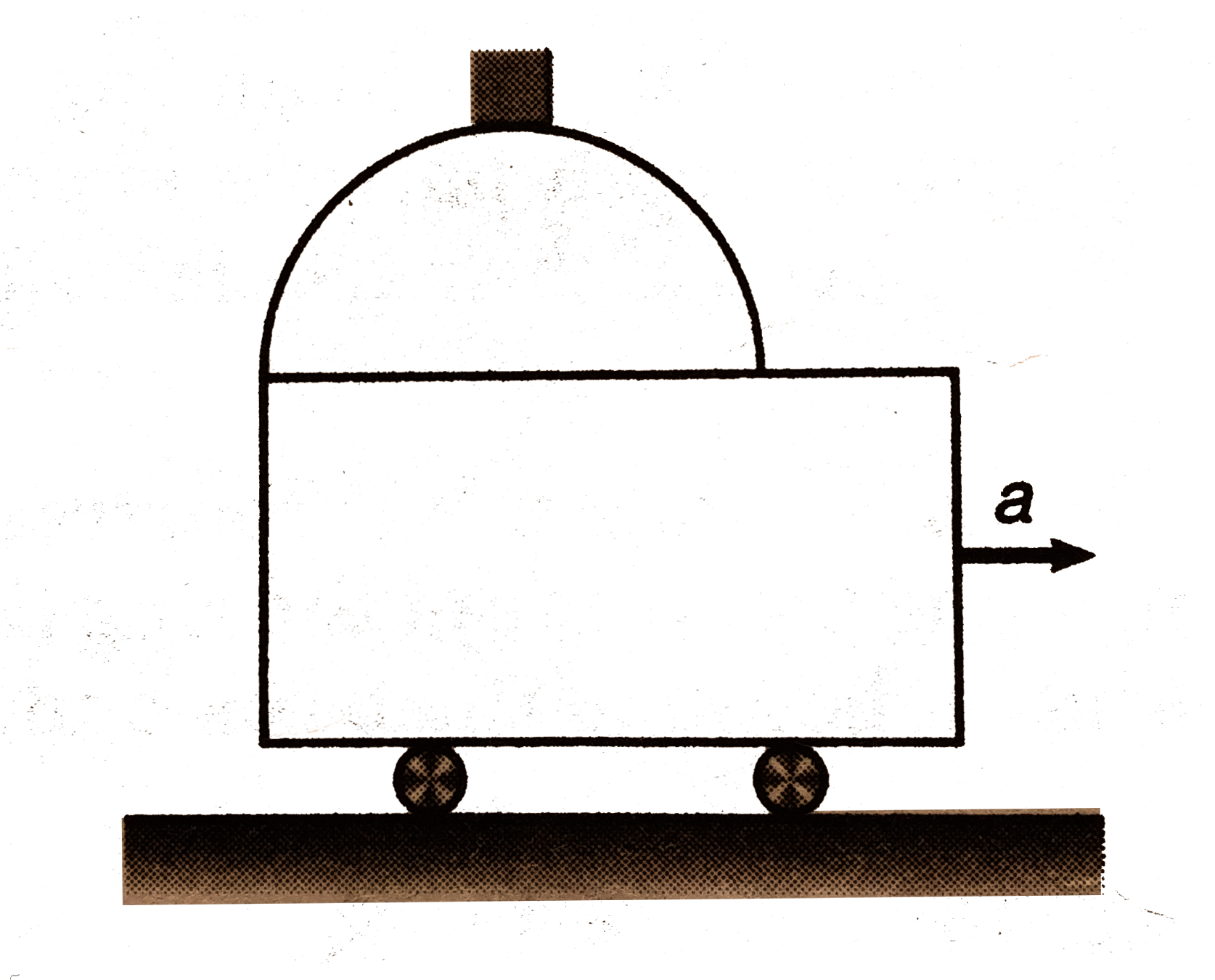
(a) Calculate the angle θ at which it loses contact with the trolly and
(b) the time taken by the mass to drop on the floor, after losing contact.
The correct Answer is:B, C
(a) Let vr be the velocity of mass relative to track at angular position θ .
From work energy theorem, KE of particle relative to track
=Work done by force of gravity+work done by pseudo force
:. 12mv2r=mg(1−cosθ)+m(2g9)sinθ
opr v2=2g(1−cosθ)+4g9sinθr
Particle leaves contact with the track where N=0
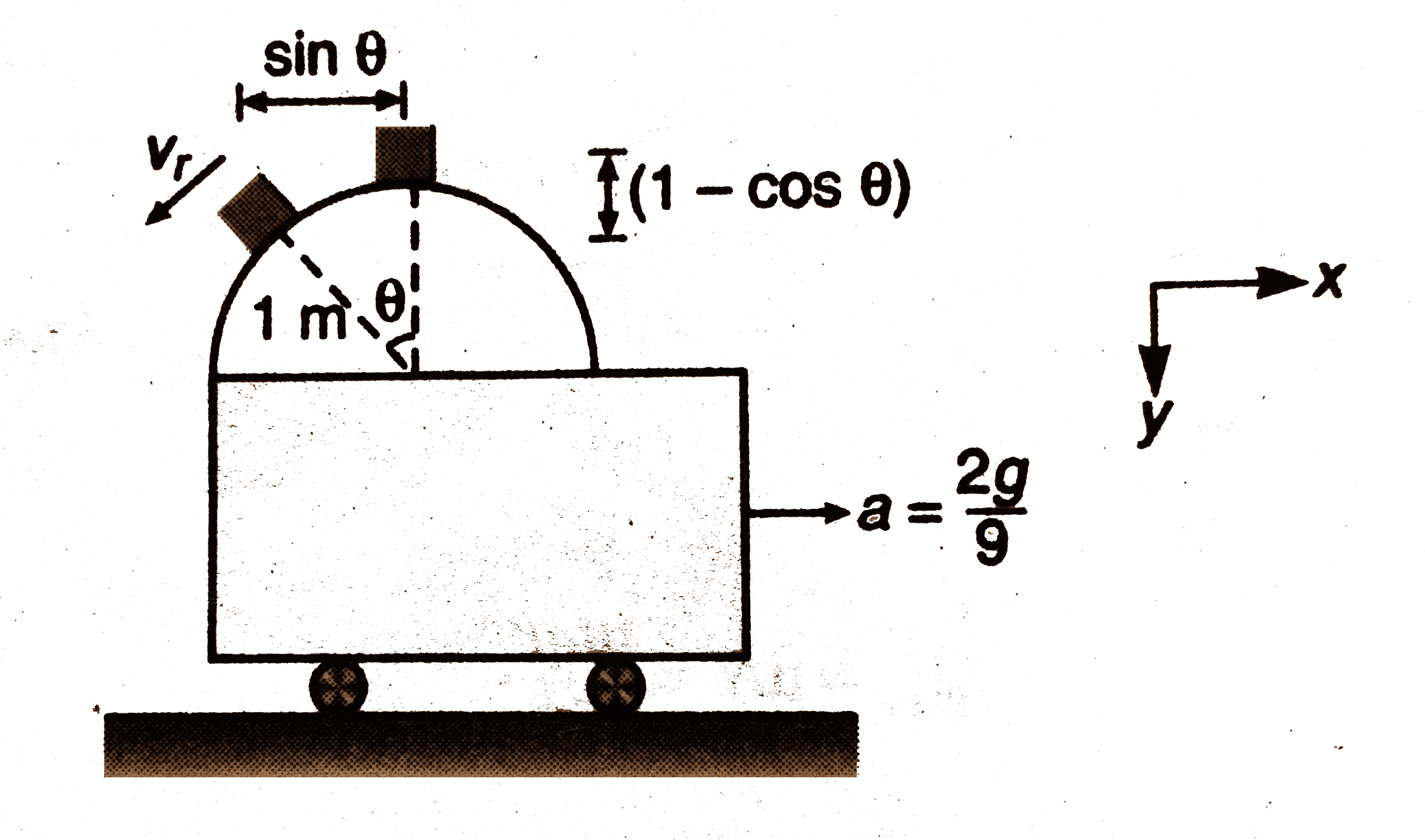
or mgcosθ−m(2g9)sinθ=mv2r
or gcosθ−2g9sinθ=2g(1−cosθ)+4g9sinθ
or 3cosθ−69sinθ2
Solving this, we get θ≈37∘
(b) From Eq. (i) we have,
vr=√2g(1−cosθ)+4g9sinθ
or vr=2.58m/satθ=37∘
Vertical component of its velocity is
vy=vrsinθ
=2.58×35
=1.55m/s
Now, 1.3=1.55t+5t2(∵s=ut+12>2)
or 5t2+1.55t−1.3=0
or t=0.38s
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:JEE Main
Explore 23 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:JEE Advanced
Explore 25 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Level 2 Subjective
Explore 13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
View Solution
Knowledge Check
The mass m slides down the track and completes the vertical circle on the smooth curved surface. The minimum value of h will be:
 ARB2 RC2.5 RD3 R
ARB2 RC2.5 RD3 RA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
 Aθ=sin−1[13(1+√1−GM3m)]Bθ=cos−1[53(1+√1−3M2m)]Cθ=cos−1[13(1+√1−3M2m)]Dθ=cos−1[13(1+√1−5M3m)]
Aθ=sin−1[13(1+√1−GM3m)]Bθ=cos−1[53(1+√1−3M2m)]Cθ=cos−1[13(1+√1−3M2m)]Dθ=cos−1[13(1+√1−5M3m)]A cube of mass M starts of rest from point 1 at a height 4R, where R is the radius of the circular track. The cube slides down the frictionless track and around the loop. The force which the track exerts on the cube at point 2 is :
 A3 MgBMgC2MgDCube will not reach the point 2
A3 MgBMgC2MgDCube will not reach the point 2
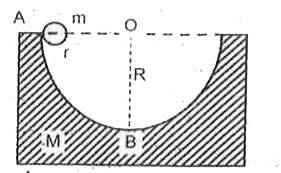
A block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionA block of mass M with a semi circular track of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A. The cylinder slips on the semicurcular frictionless track. How far has the block moved when the cylinder reaches the bottom of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View Solution
