All surfaces shown in figure are smooth. Wedges of mass 'M' is free to move. Block of mass 'm' is given a horizontal velocity v0 as shown. Find the maximum height 'h' attained by 'm' (over the wedges or outside it).

The correct Answer is:A
At maximum height vertical component of velocity of 'm' wil be zero. It will have only horizontal component of velocity and this is equal to the horizontal component of 'M' also (think why?). So at the highest point figure is like this:
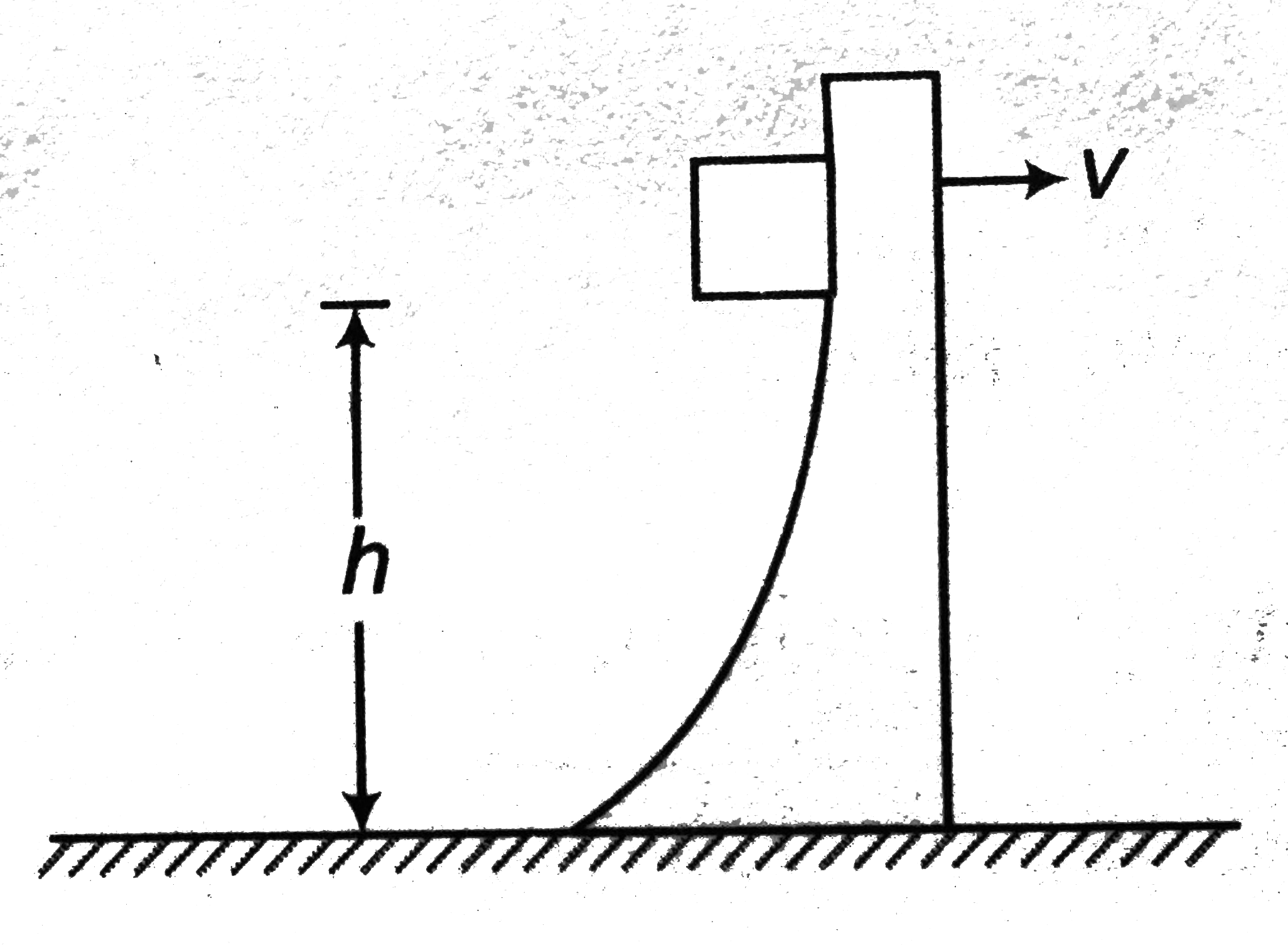
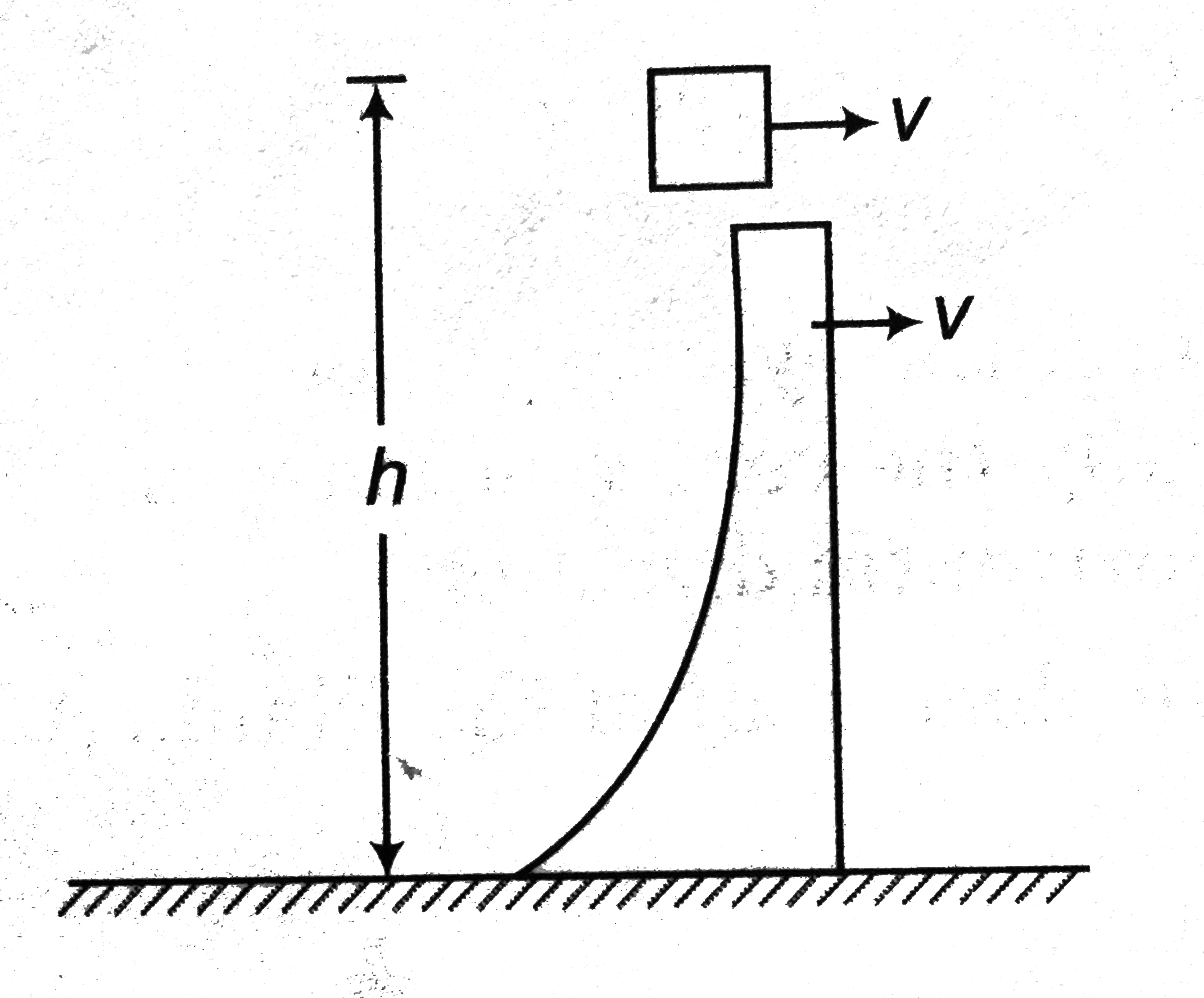
Applying law of conservation of linear momentum in horizontal direction,
pi=pf
⇒mv0=(M+m)v ...(i)
Now, applying law of conservation of mechanical energy,
Ei=Ef
∴12mv20=12(M+m)v2+mgh ...(ii)
We have two unknowns v and h.
So, we can find the value of 'h' by solving these two equations. ltbr> Exercise: Solve these two equations to find the value of 'h'.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - MiscellaneousExamples9videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
A smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?
 View Solution
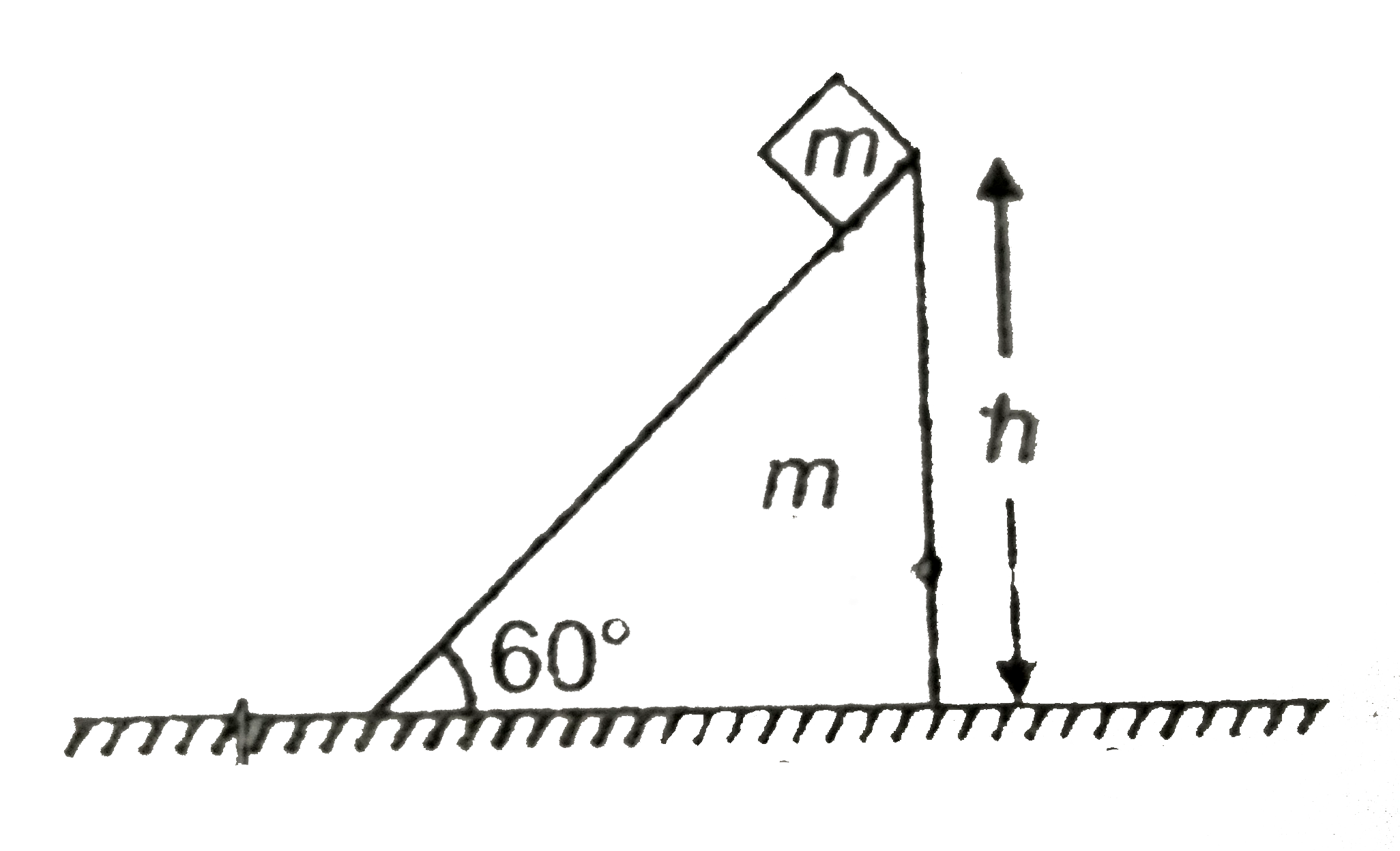
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ - Question 2 - Select One
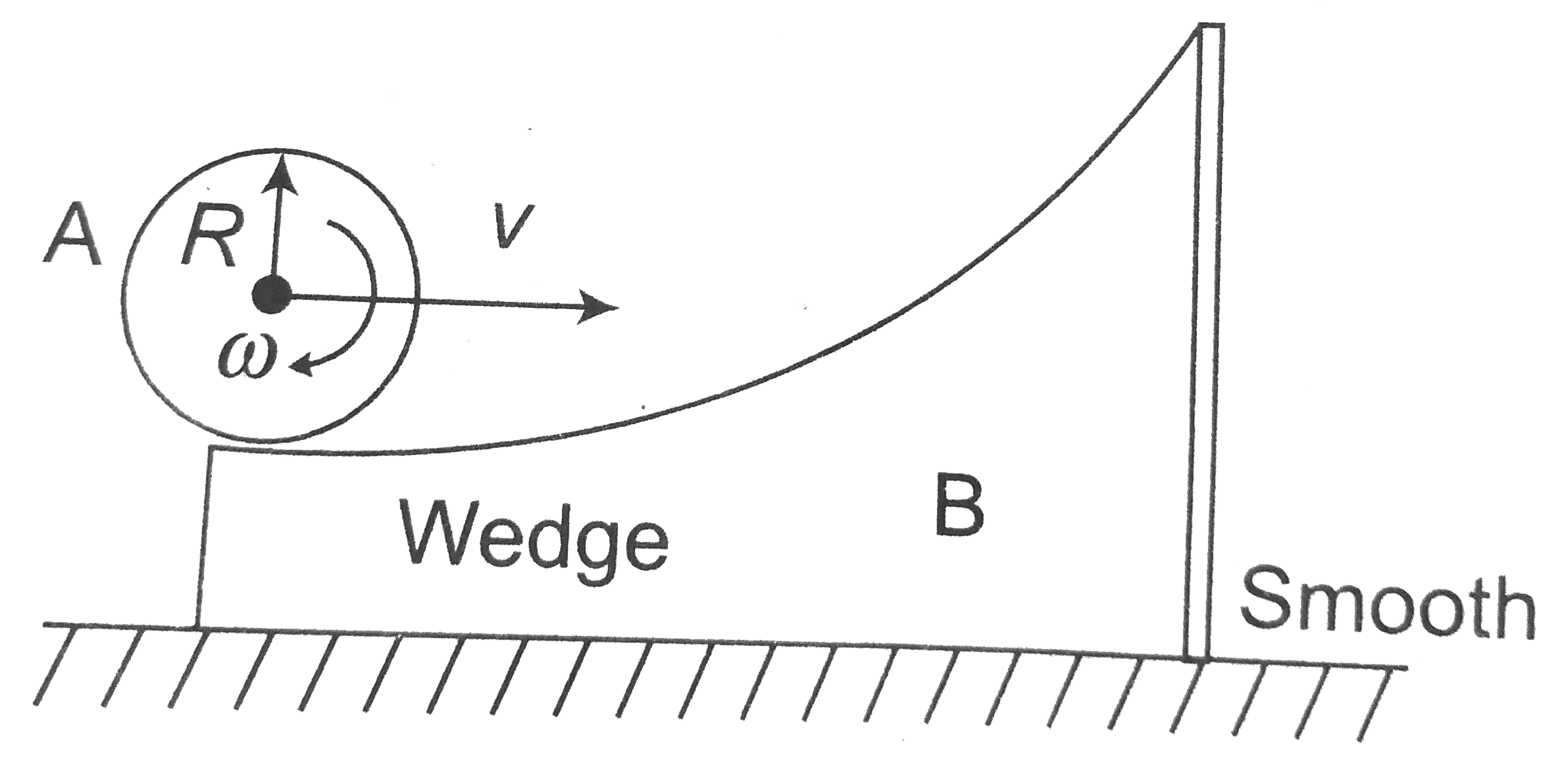
In the figure shown, a cylinder A is initially rolling with velocity v on the horizontal surface of the wedge B (of same mass as A). All surfaces are smooth and B has no initial velocity. Then maximum height reached by cylinder on the wedge will be.
 .Av2/4gBv2/gCv2/2gDv2/8
.Av2/4gBv2/gCv2/2gDv2/8 - Question 3 - Select One
A small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
 AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
A particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
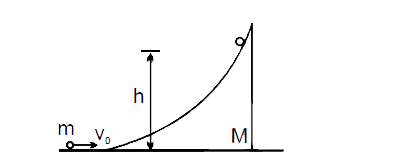
The maximum height h attained by the particle isView SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
 View Solution
View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?
 View Solution
View SolutionIn the fig 4 .25 shown, if all the surfaces are smooth , then determine the maximum height h attained by the block on the wedge, assuming it to be very large .
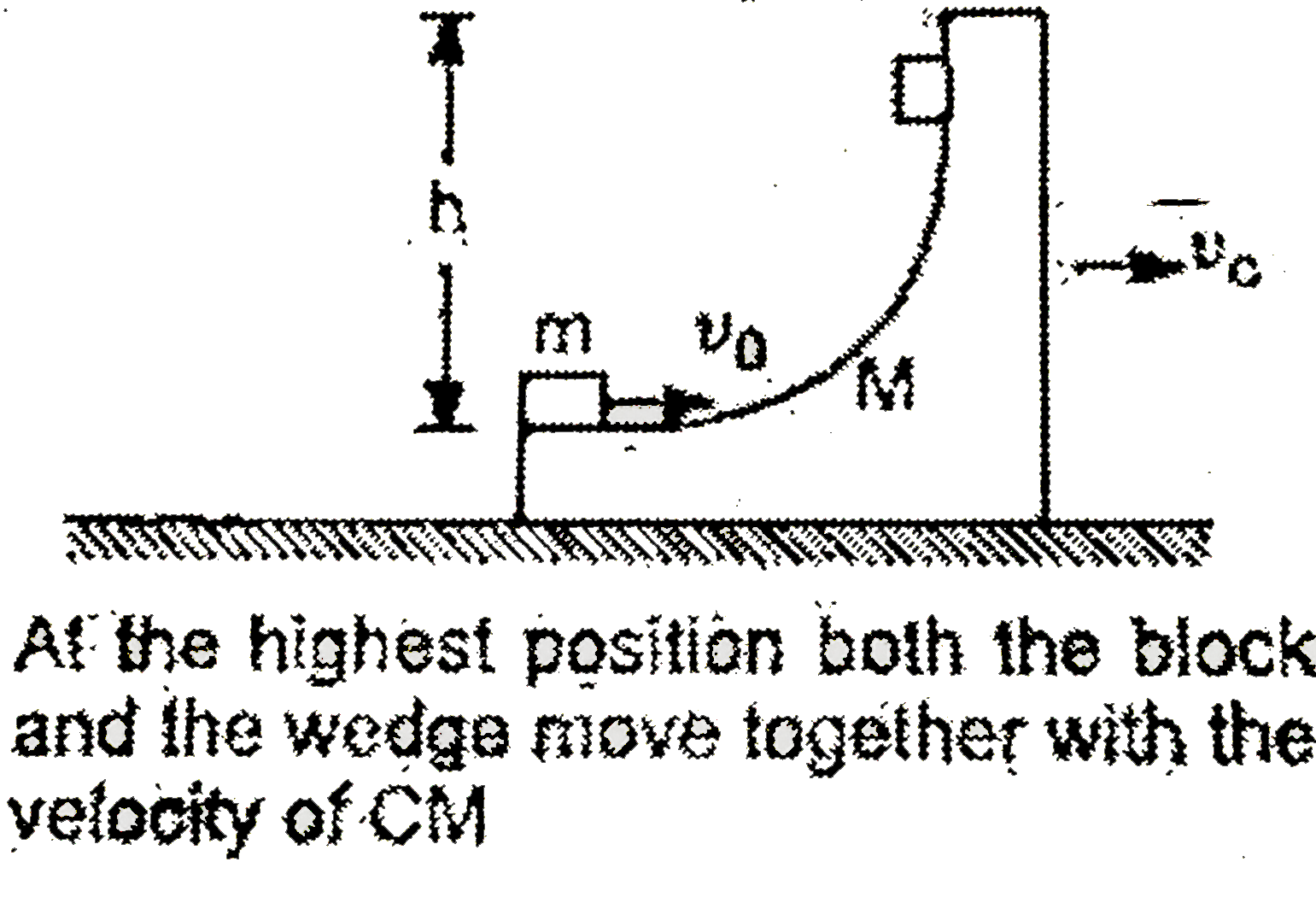 View Solution
View Solution_2019_CBT4_E01_069_Q01.png)
A wedge of mass 4m is initially at rest on frictionles horizotnal surface. A small block of mass m moving with speed v0 and climbs on wedge. Find maximum height achieved by blockView Solution

