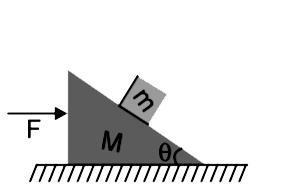
In the fig 4 .25 shown, if all the surfaces are smooth , then determine the maximum height h attained by the block on the wedge, assuming it to be very large .
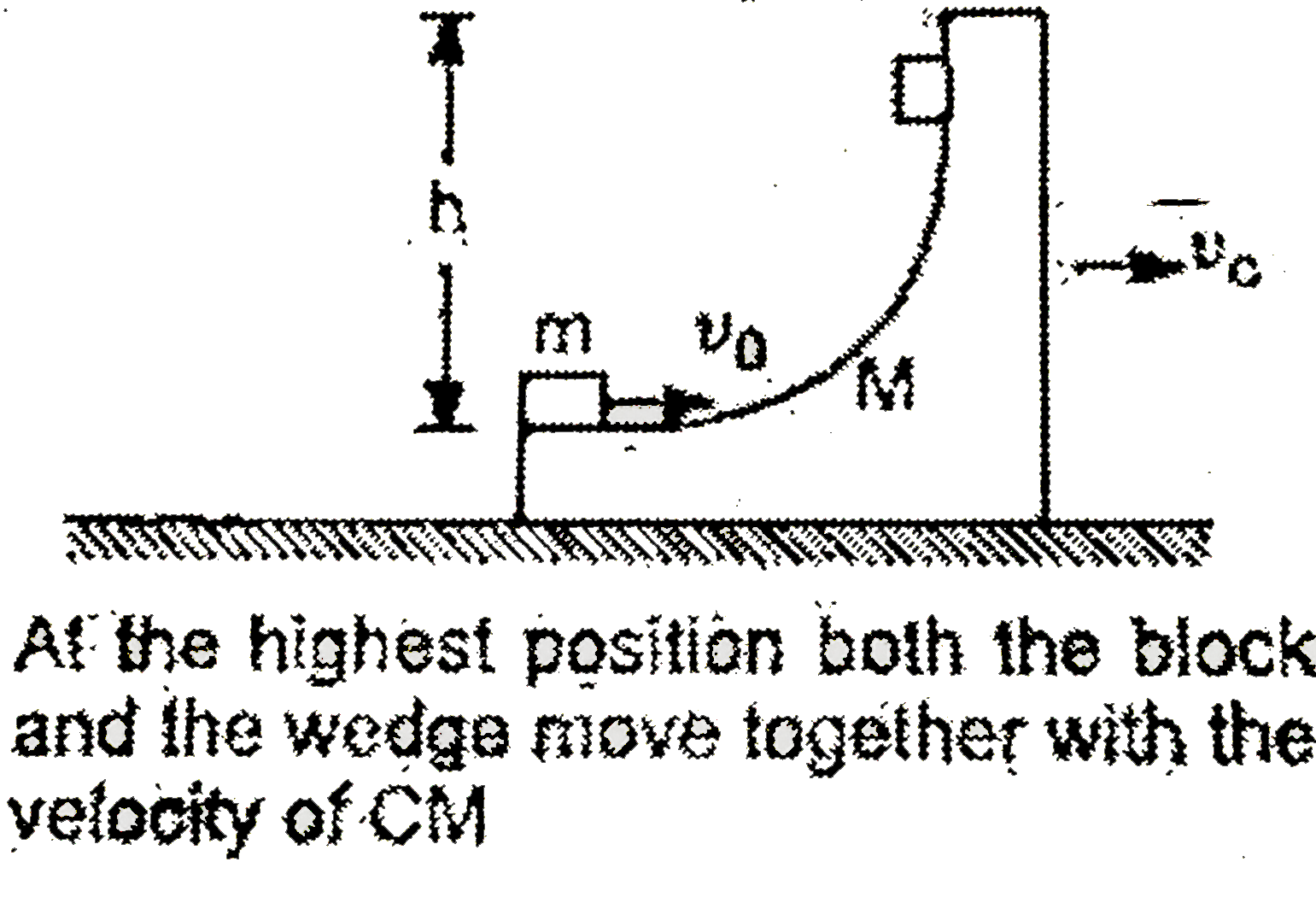
Step by step video & image solution for In the fig 4 .25 shown, if all the surfaces are smooth , then determine the maximum height h attained by the block on the wedge, assuming it to be very large . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example50videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Level 1110videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
Similar Questions
.
Knowledge Check
- Question 1 - Select One
Ram is preparing for IIT JEE. He sets on to tackle a typical problem in mechanics. He sees that the wedge is kept on a smooth ground and it's inclined surface is also smooth. A block is projected on it as shown. Both the block and wedge have equal mass. Can you help him find the answer to following three question?
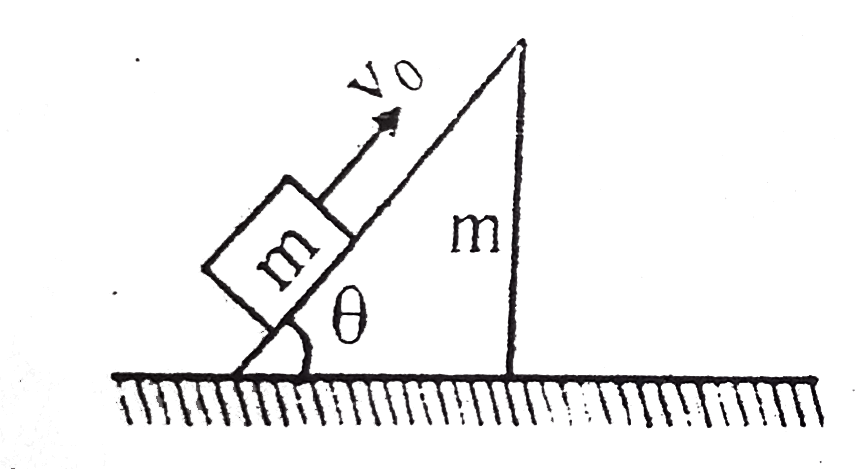He sets on to find the maximum height attained by the block, assuming the block does not fall off to the other side. Which of the following equation is correct.Amgh=12mv20 (by conservation of energy) where h is maximum height of the block.B02=v20−2gsinθ×s where is maximum displacement along the inclined surfaceCmv0=mv+mv (by conservation of momentum) and 12mv20=12mv2+12mv2+mghDNone of these - Question 2 - Select One
In the figure shown, a cylinder A is initially rolling with velocity v on the horizontal surface of the wedge B (of same mass as A). All surfaces are smooth and B has no initial velocity. Then maximum height reached by cylinder on the wedge will be.
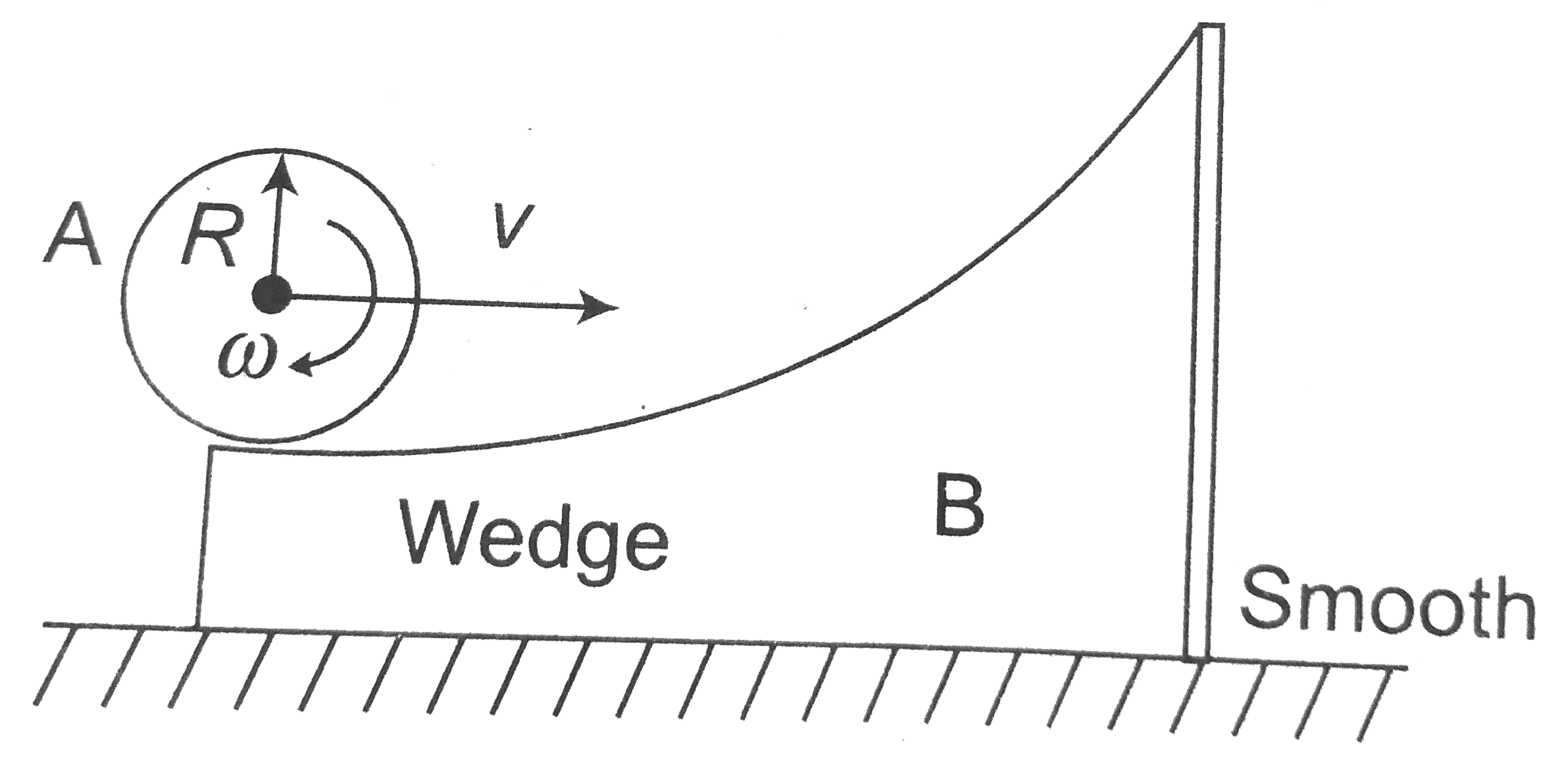.Av2/4gBv2/gCv2/2gDv2/8 - Question 3 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Assuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.
View SolutionIn the system shown in the figure all surfaces are smooth and both the pulleys are mass less. Block on the incline surface of wedge A has mass m. Mass of A and B are M = 4 m and M0=2 m respectively. Find the acceleration of wedge A when the system is released from rest.
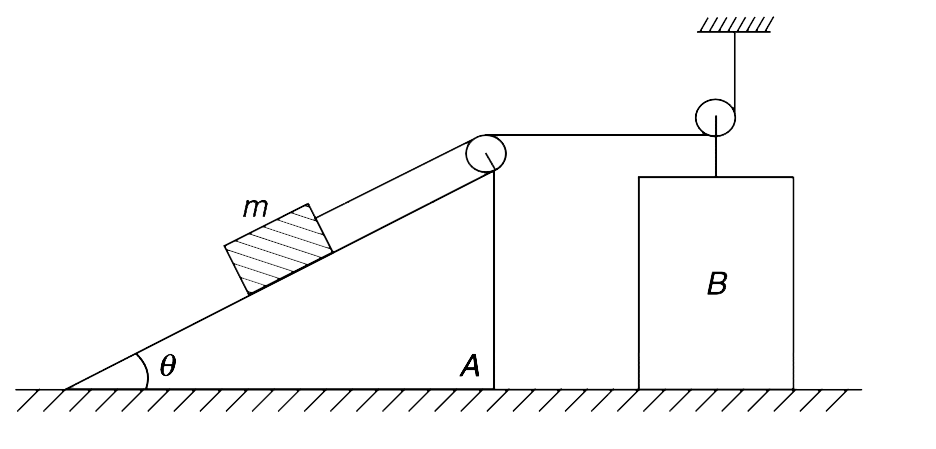View SolutionA ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.
Let h be the maximum height from ground reached by ball after leaving track at B. Then,View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-
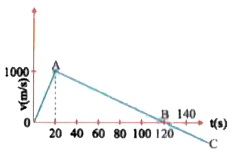View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-
View Solution
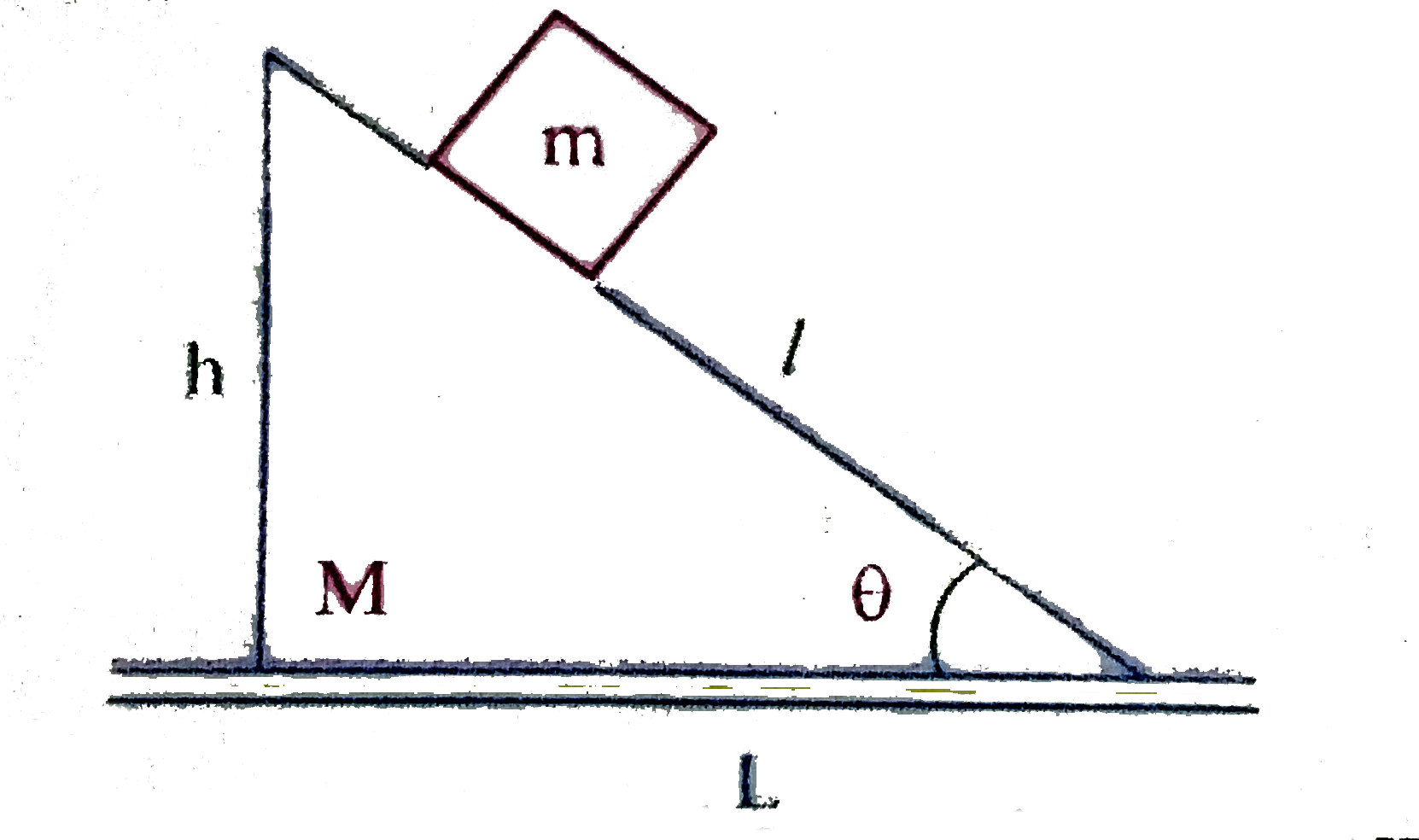