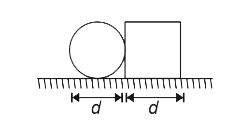
A square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of sqaure.

The correct Answer is:A, D
d=A1d1+A2d2A1+A2
Here, d=distance of centre of mass fromO.
∴d=(a2)(0)+(π4a2)(a)a2+(π/4)a2
=(ππ+4)a
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.3
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - MiscellaneousExamples
9 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
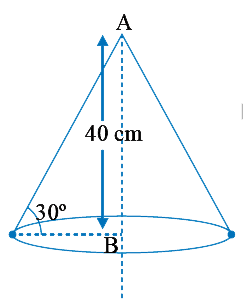
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
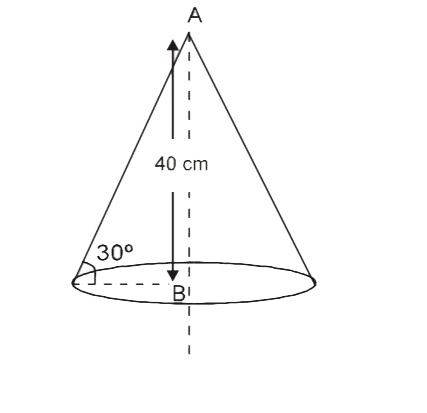
View Solution
Knowledge Check
The distance of centre of mass from O is
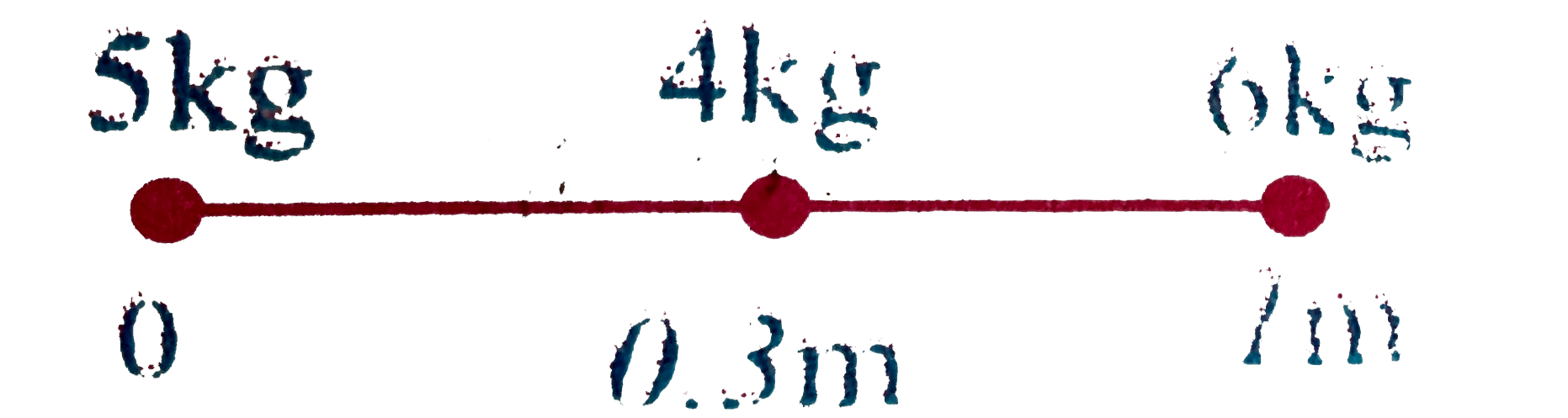 A0.21mB0.35mC0.42mD0.48m
A0.21mB0.35mC0.42mD0.48mA square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of plate as shown. Then center of mass of the combination will be (assume same mass per unit area for the two plates):
 A2d2+π left to the center of the discB2d2+π right to the center of the discC4d4+π right to the center of the discD4d4+π left to the center of the disc
A2d2+π left to the center of the discB2d2+π right to the center of the discC4d4+π right to the center of the discD4d4+π left to the center of the discA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
Fron a sqaure plate of side a,a quarter circular disc of radius a is removed as shown in figure. Find the coordinates of centre of mass of the remaining part.

View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionThree identical spheres each of radius R are placed touching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
 .
.
View SolutionA square hole is punched out of a circular lamina of diameter 4 cms., the diagonal of the square being a radius of the circle. Centroid of the remainder from the centre of the circle is at a distance
View Solution
