Assertion: An object of mass m1 and another of mass m2(m2>m1) are released from certain distance. The objects move towards each other under the gravitational force between them. In this motion, centre of mass of their system will continuously move towards the heavier mass m2.
Reason: In a system of a heavier and a lighter mass, centre of mass lies closer to the heavier mass.
(a) If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b) If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false but the Reason is true.
The correct Answer is:D
Centre of mass remains stationary.
Similar Questions
Calculate the position of centre of mass of a system consisting of two particles of masses m_1 and m_2 separated by a distance L apar, from m_1?
View Solution10 Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
Am1m2vBZeroC(m1−m2)vm1+m2Dm2m1v - Question 2 - Select One or More
Two objectes of mass m and 4m are at rest at and infinite seperation. They move towards each other under mutual gravitational attraction. If G is the universal gravitational constant. Then at seperation r
Athe total energy of the two objects is zeroBtheir relative velocity of approach is (10GMr)1/2 in magnitudeCthe total kinetic energy of the objects is 4Gm2rDnet angular momentum of both the particles is zero about any point - Question 3 - Select One
Two bodies of masses 2kg and 4 kg are moving with velocities 20 m/s and 10m/s towards each other due to mutual gravitational attraction . What is the velocity of their centre of mass ?
A5.3ms−1B6.4ms−1CZeroD8.1ms−1
Figure. Shown a ring of mass M1 ans a sphere of mass M2 separated by a distance √3R. A small object of mass m is displaced from A to B. Find the work done by gravitational forces.
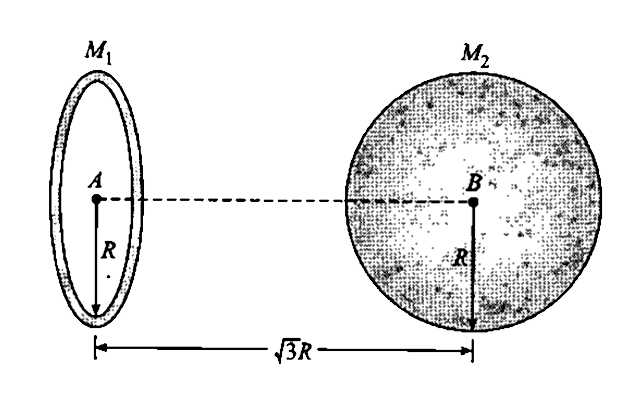 View Solution
View SolutionTwo particles of masses m and M are initially at rest at an infinite distance part. They move towards each other and gain speeds due to gravitational attracton. Find their speeds when the separation between the masses becomes equal to d.
View SolutionTwo bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionIf the distance between two point masses m1 and m2 is d, then distance of its centre of mass from m2 will be mod
View SolutionA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
View Solution

