Two bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
5ms−1
6ms−1
8ms−1
zero
The correct Answer is:D
To solve the problem of finding the velocity of the center of mass for two bodies of different masses moving towards each other, we can follow these steps:
Step 1: Identify the masses and velocities
We have two bodies:
- Mass of the first body, m1=2kg with velocity v1=2m/s (towards the right)
- Mass of the second body, m2=4kg with velocity v2=−10m/s (towards the left, hence negative)
Step 2: Use the formula for the velocity of the center of mass
The formula for the velocity of the center of mass Vcm is given by:
Vcm=m1v1+m2v2m1+m2
Step 3: Substitute the values into the formula
Substituting the values we identified:
Vcm=(2kg⋅2m/s)+(4kg⋅−10m/s)2kg+4kg
Step 4: Calculate the numerator and denominator
Calculating the numerator:
=(2⋅2)+(4⋅−10)=4−40=−36
Calculating the denominator:
=2+4=6
Step 5: Calculate the velocity of the center of mass
Now substituting back into the equation:
Vcm=−366=−6m/s
Step 6: Interpret the result
The negative sign indicates that the center of mass is moving in the direction of the second body (the 4 kg mass moving left). However, since the question asks for the magnitude of the center of mass velocity, we can say:
|Vcm|=6m/s
Conclusion
The velocity of the center of mass is 6m/s towards the left.
We have two bodies:
- Mass of the first body, m1=2kg with velocity v1=2m/s (towards the right)
- Mass of the second body, m2=4kg with velocity v2=−10m/s (towards the left, hence negative)
The formula for the velocity of the center of mass Vcm is given by:
Vcm=m1v1+m2v2m1+m2
Substituting the values we identified:
Vcm=(2kg⋅2m/s)+(4kg⋅−10m/s)2kg+4kg
Calculating the numerator:
=(2⋅2)+(4⋅−10)=4−40=−36
Calculating the denominator:
=2+4=6
Now substituting back into the equation:
Vcm=−366=−6m/s
The negative sign indicates that the center of mass is moving in the direction of the second body (the 4 kg mass moving left). However, since the question asks for the magnitude of the center of mass velocity, we can say:
|Vcm|=6m/s
The velocity of the center of mass is 6m/s towards the left.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-II(C.W.)64videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-III66videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - C.U.Q.83videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
2 bodies of different masses of 2 kg and 4 kg are moving with velocities 20m/s and 10 m//s towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s respectively along same direction. Then the velocity of their centre of mass will be
View Solution
Knowledge Check
- Question 1 - Select One
Two bodies of masses 2kg and 4 kg are moving with velocities 20 m/s and 10m/s towards each other due to mutual gravitational attraction . What is the velocity of their centre of mass ?
A5.3ms−1B6.4ms−1CZeroD8.1ms−1 - Question 2 - Select One
Two bodies of masses 2 kg and 4 kg are moving with velocities 2 m s−1 and 10 m s−1 towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
A5.3ms−1B6.4ms−1CzeroD8.1ms−1 - Question 3 - Select One
2 bodies of different masses of 2 kg and 4 kg are moving with velocities 20m/s and 10 m//s towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
A5ms−1B6ms−1C8ms−1DZero
Two bodies of masses 10kgand2kg are moving with velocities (2ˆi−7ˆj+3ˆk)and(−10ˆi+35ˆj−3ˆk)m/s respectively. Calculate the velocity of their centre of mass.
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
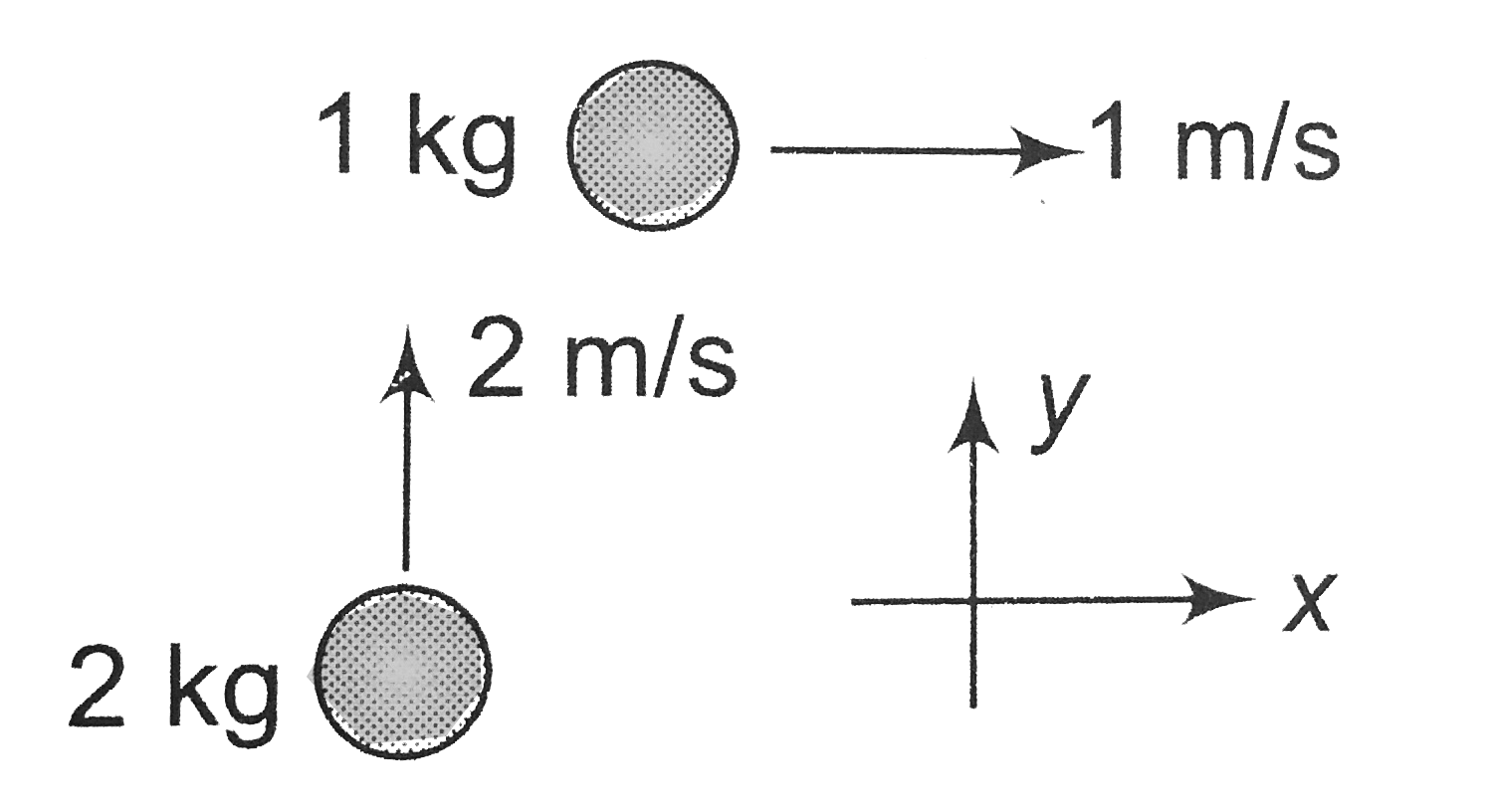 View Solution
View SolutionA body of mass 20 kg is moving with a velocity of 2v and another body of mass 10 kg is moving with velocity V along same direction. The velocity of their centre of mass is
View Solution

