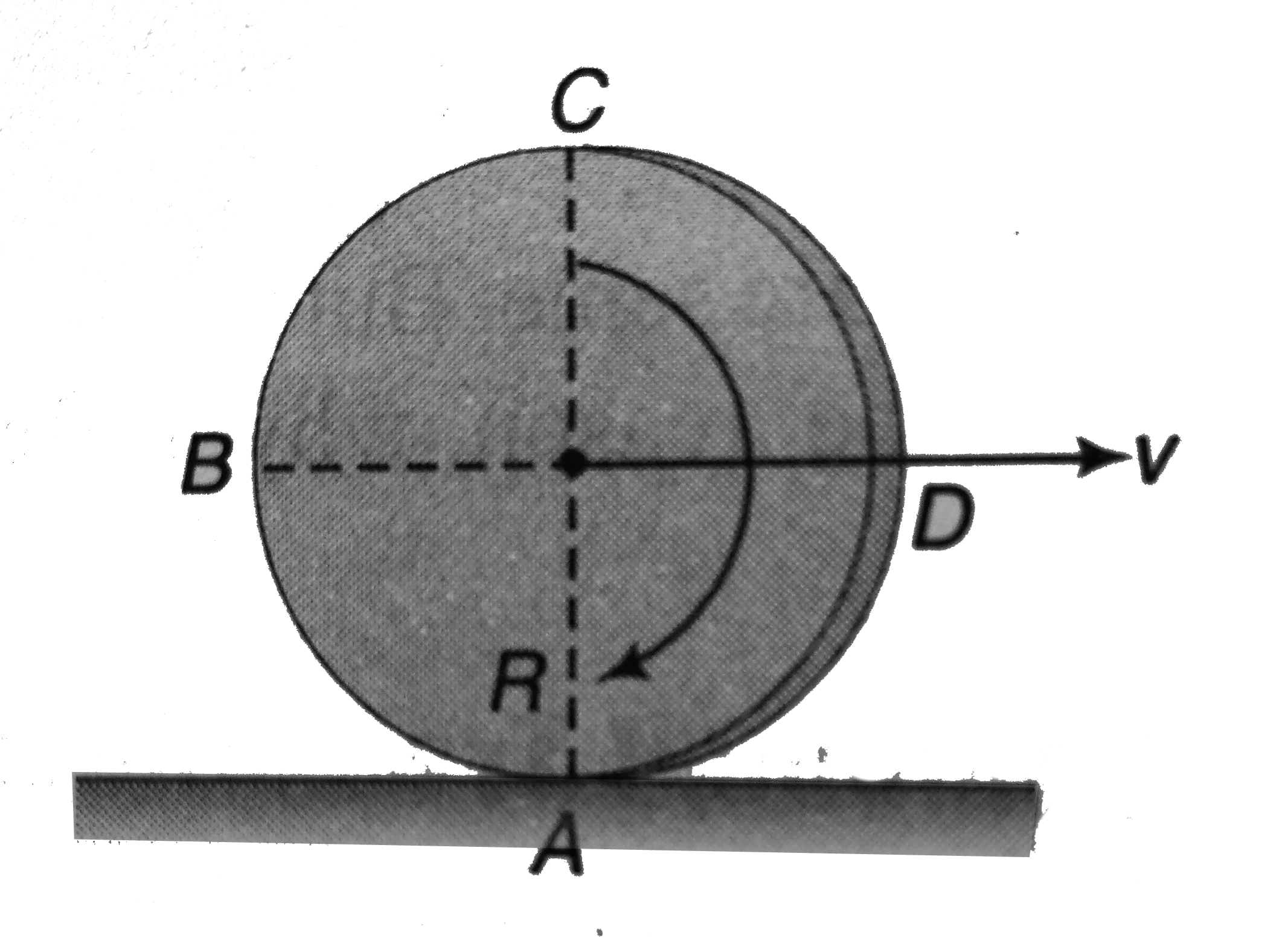
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
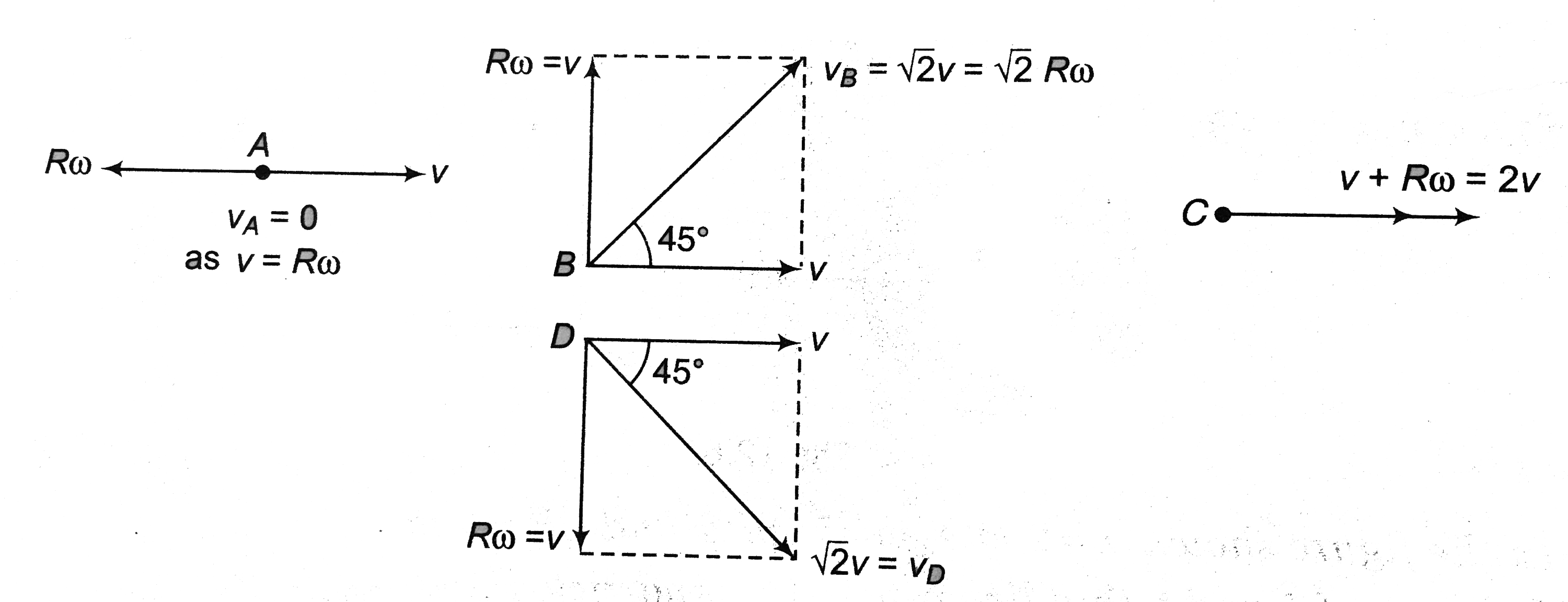

As stated in above article, velocity of ay point of the rigid body in rotation plus translationn is the vector sum of v (the velocity of centre of mass) and rω. Here, r is the distance of the point under consideration from the centre of mass of the body. direction of this rω is perpendicular to the line joining the point with centre of mass in the sense of rotation. Based on this, velocities of points A, B ,C and D are as shown below.
thus, VA is zero, velocity of B and D is √2v or √2Rω and velocity of C is 2 v or 2Rω in the direction shown in figure.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions

A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
View Solution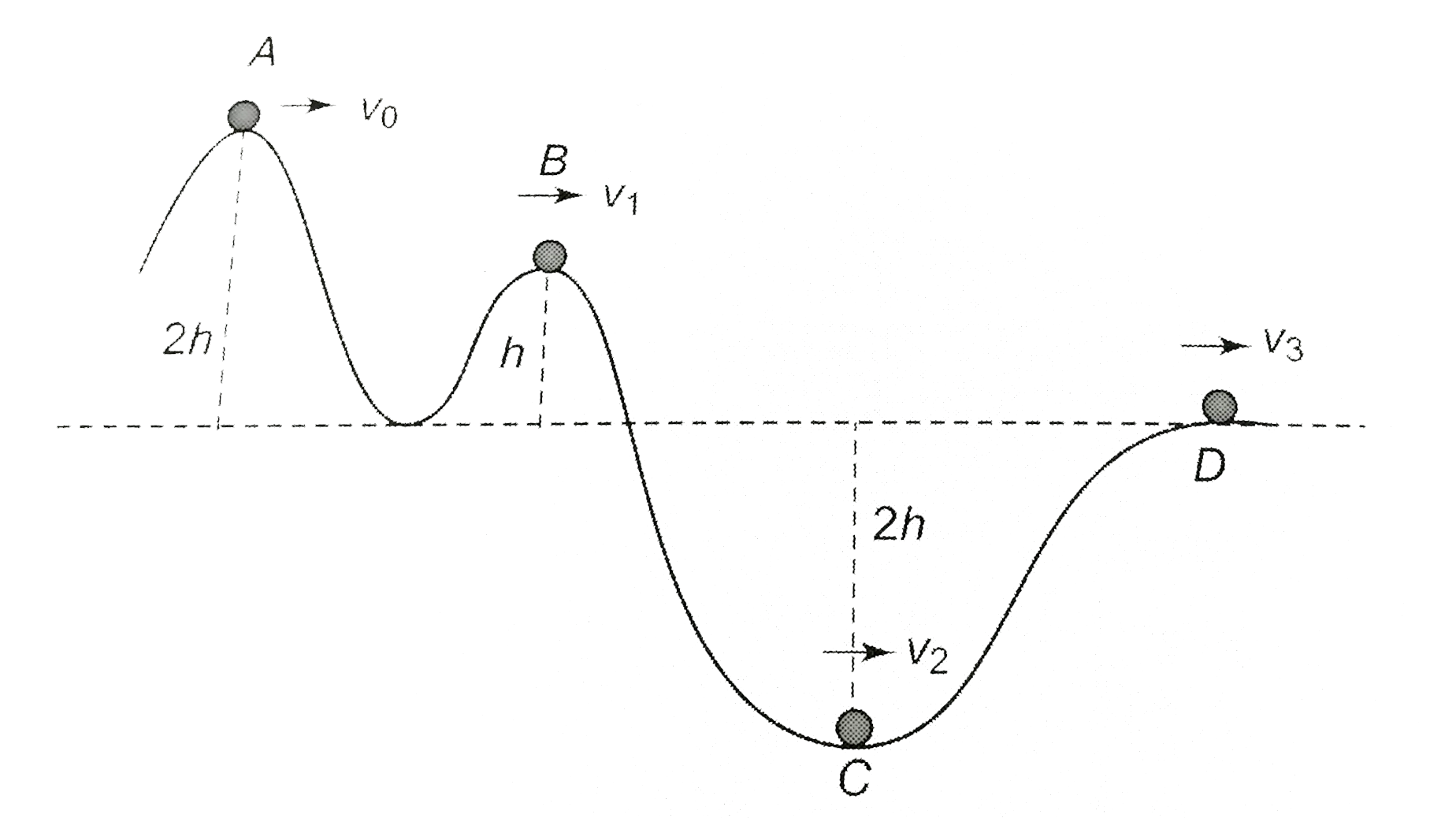
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and D
View Solution
Knowledge Check
Relation between Linear velocity (v) and Angular velocity (ω)
Av=rωBω=vωCr=vωDv=ωrA circular disc of radius R is rotating about its axis O with a uniform angular velocity ωrad s−1 as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is
 AzeroBRωsin(θ2)C2Rωsin(θ2)D√3Rωsin(θ2)
AzeroBRωsin(θ2)C2Rωsin(θ2)D√3Rωsin(θ2)A uniform circular disc placed on a rough horizontal surface has initially a velocity v0 and an angular velocity ω0 as shown in the figure. The disc comes to rest after moving some distance in the direction of motion. Then v0rω0 is.
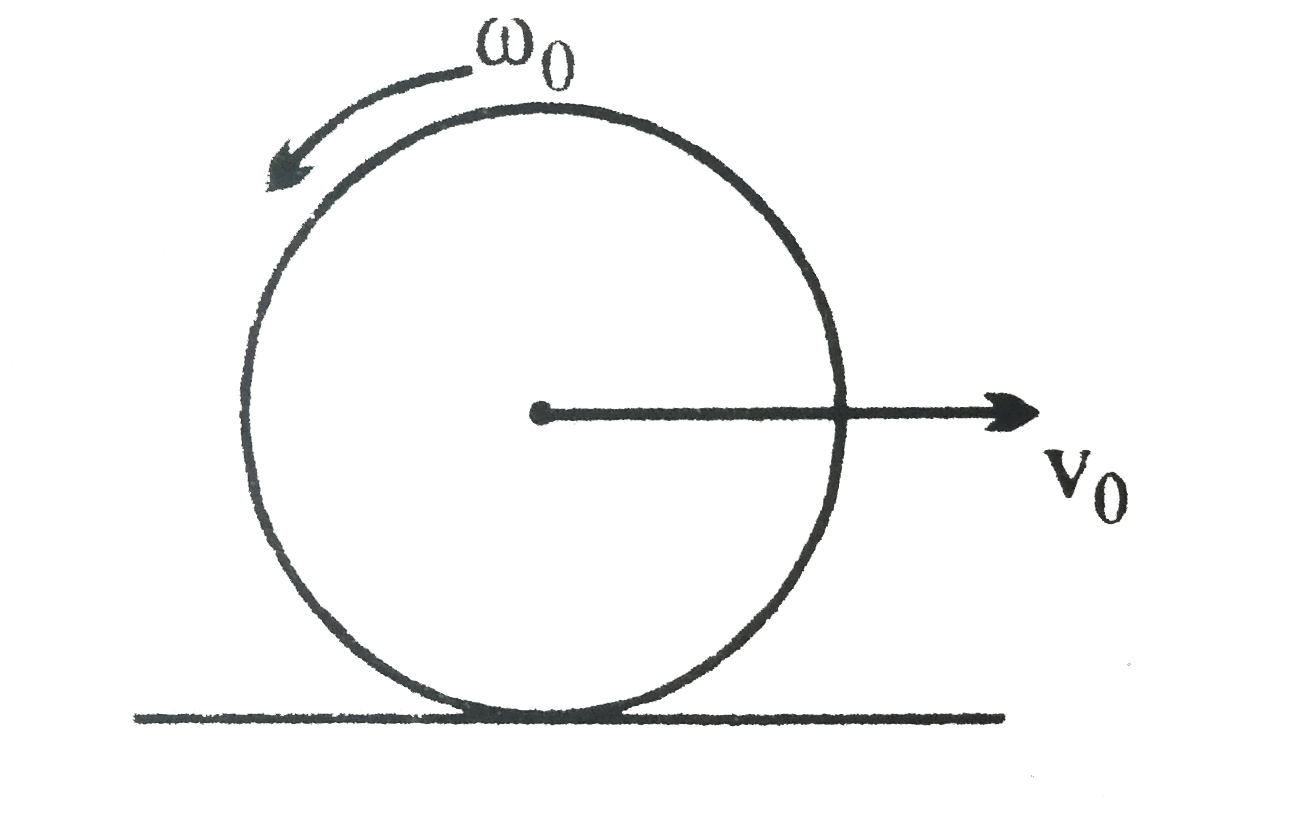 .A1/2B1C3/2D2
.A1/2B1C3/2D2
A tire of radius R rolls on a flat surface with angular velocity omega and velocity υ as shown in the diagram. If υ>ωR, in which direction does friction from the tire act on the road?
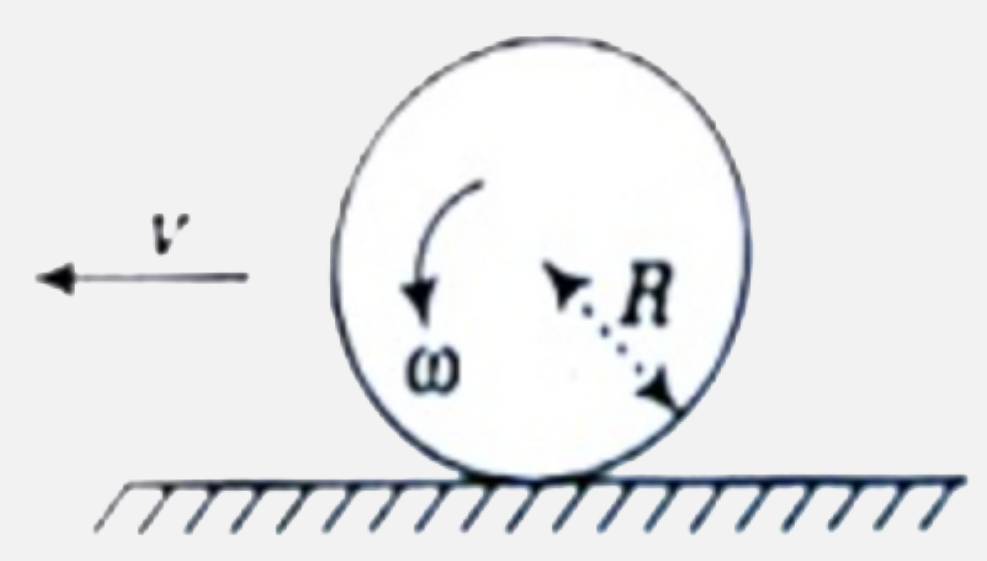
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA uniform circular disc placed on a horizontal rough surface has initially a velocity v0 and an angular velocity ω0 as shown in the figure. The disc comes to rest after moving some distance in the direction of motion. Then v0/ω0 is :

View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that

View SolutionA disc is given an angular velocity ω0 and a linear velocity v0 as shown in the figure. It is released on a rough horizontal surface of friction coefficient μ. Mark the correct statement (ω0=3v0/R)

View Solution