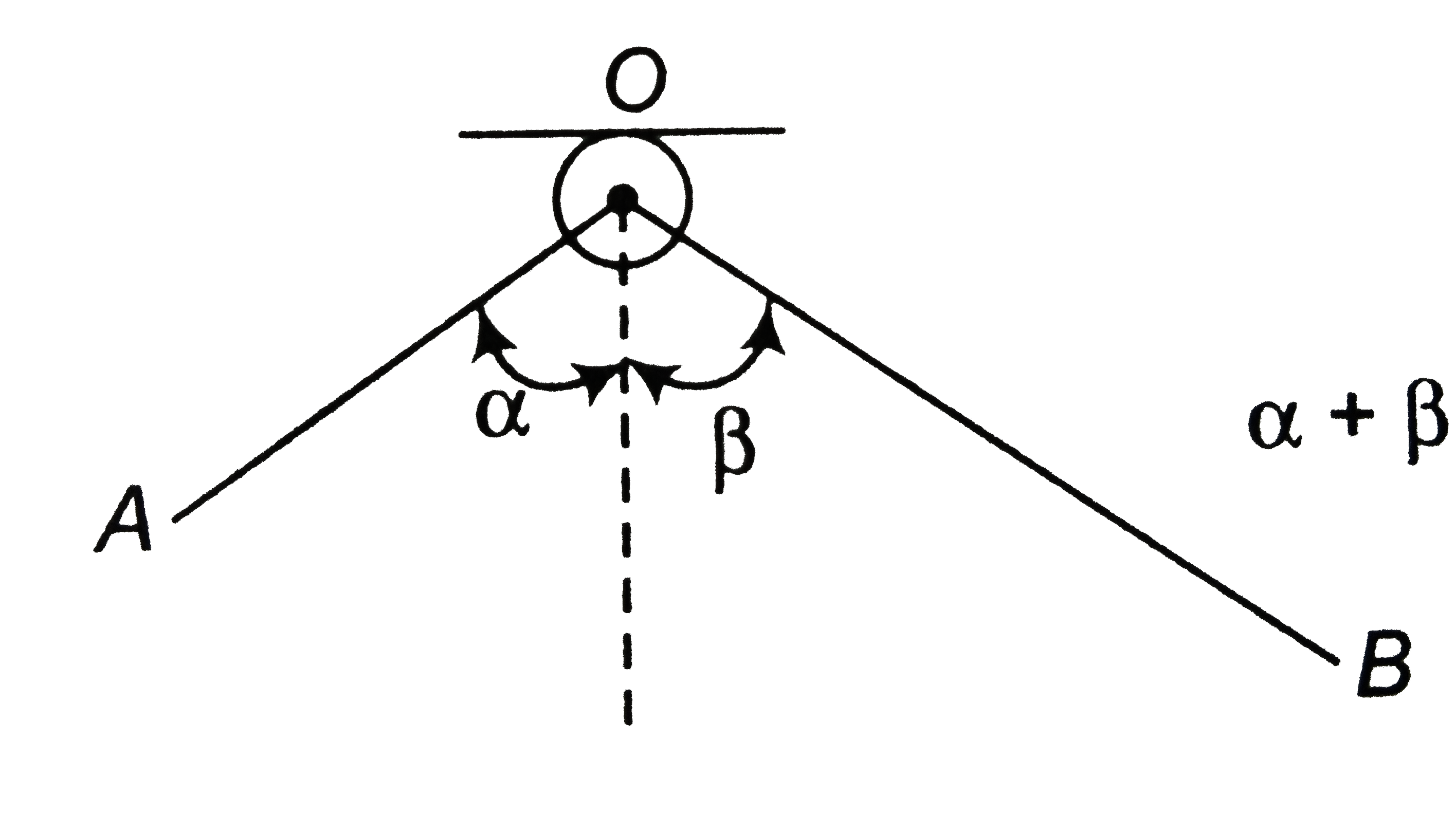
A uniform L shaped rod of mass 3 m is hinged at point O. length OB is two times the length OA. It is in equilibriu.
Find
(a). Relation between α and β
(b). Net hinge force.
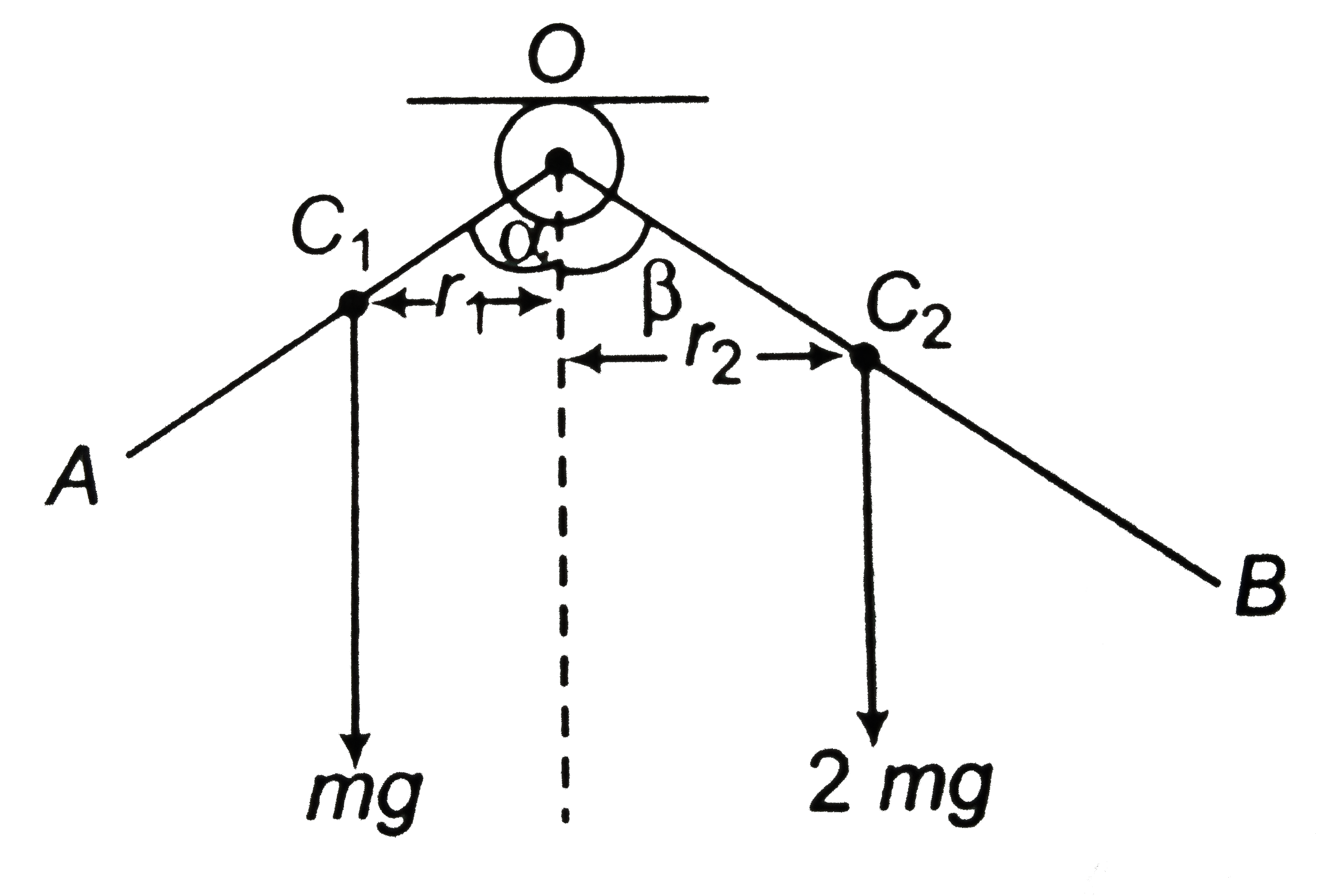
(a). Length OB is two times the length OA. Therefore, mass of OB is 2m and that of OA is m ad their weighht will act at their centres (as the rod is uniform)
If total length is 3l then
OA=l ⇒OC1=OA2=l2
and r1=OC1sinα=l2sinα
OB=2l ⇒OC2=OB2=l
and r2=OC2sinβ=lsinβ
net torque about O=0
⇒ anticlockwise torque of mg= clockwise torque of 2 mg
⇒(mg)r1=(2mg)r2
⇒mg(l2sinα)=(2mg)lsinβ
or sinαsinβ=4 is the required relation between α and β
(b). net force on the rod is also zero. Therefore, hinge force is 3 mg (=mg+2mg) in upward direction.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod AB of mass 2kg is hinged at one end A. The rod is kept in the horizontal position by a massless string tied to point B. Find the reaction of the hinge (in N) on end A of the rod at the instant when string is cut. (g=10m/s2)

View SolutionA uniform straight rod of mass ' m (kg)&≤n>hLish∈≥dato≠end.Itisee→oscillate∈verticalpla≠.Ap∮mass(mkg)isaached→itatadistancexomtheh∈≥.Thevalueofxforwhichtimeperiodofoscillationswillbeminiμmis(L)/(n).F∈dn.((Use:) sqrt((7)/(3))=1.5)
View Solution
Knowledge Check
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA uniform L-shaped rod of mass 2m and length 2L, hangs from a hinge as shown (AO is horizontal and OB is vertical). If it is released from the position shown, then find the maximum angular velocity acquired by the end.
A√3glB√3gl(√2−1)C√3g2l(√2−1)D√3g2l(√2+1)A rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
Amg/2B2mgCmg/2√3D√3mg
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
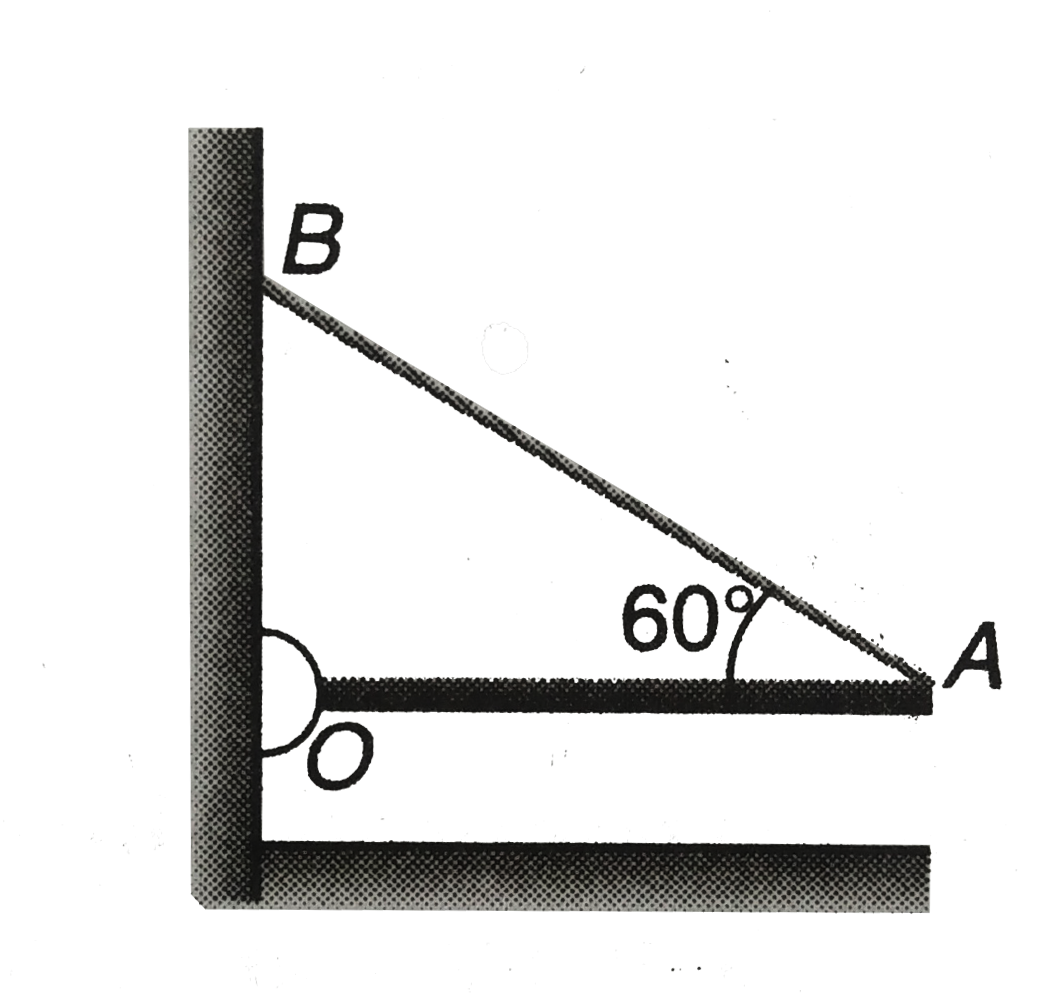
View SolutionA rod OA of mass 4kg is held in horizontal position by a massless string AB as shown in figure. Length of the rod is 2m. Find
(a) tension in the string
(b) net force exerted by hings on the rod. (g=10m/s2)
View SolutionA uniform rod of mass M and length l is hinged at point O and is free to rotate on a horizontal smooth surface. Point O is at a distance of l4 from one end of the rod. A sharp impulse P0=2√130kgm/s is applied along the surface at one end of the rod as shown in figure [tanθ=97]
(a) Find the angular speed of the rod immediately after the hit
(b) Find the impulse on the rod due to the hinge.

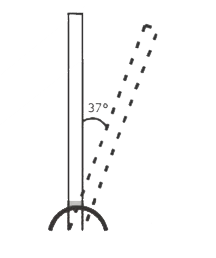
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View Solution
