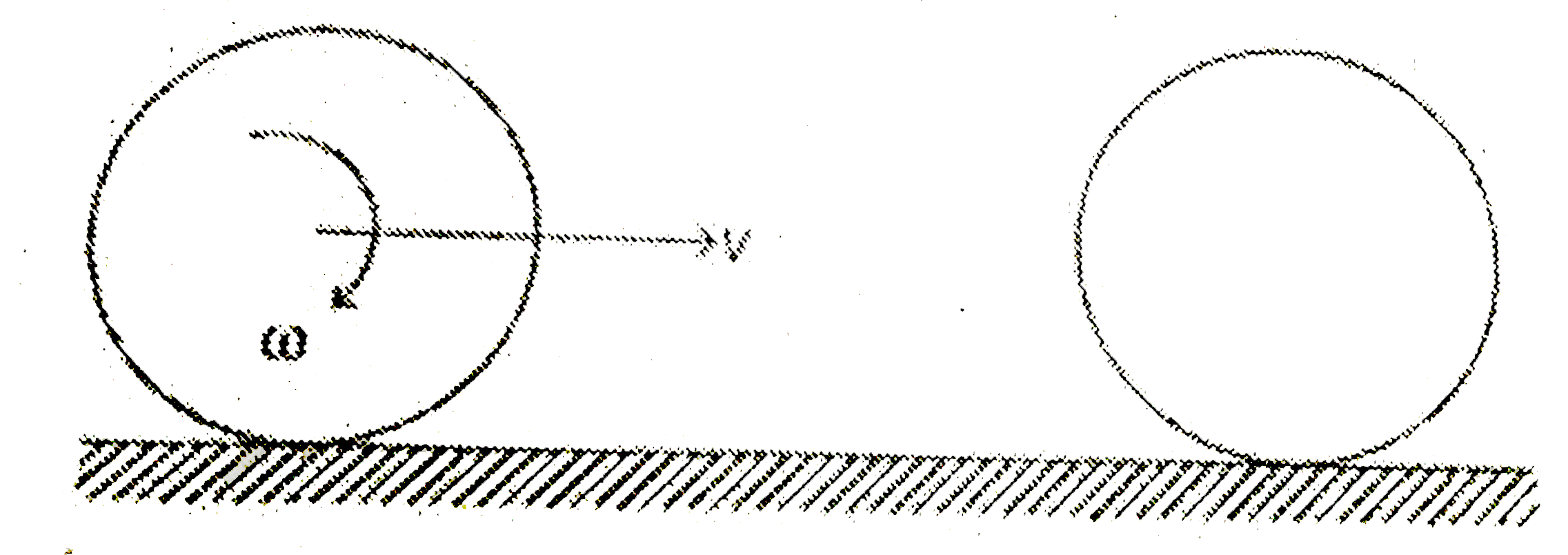
A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
it will move with a speed v initiall
its motion will be rolling with slipping initially and its rotational motion will stop momentarily at some instant.
its motion will be rolling without slipping only after some time
all of the above.

v=Rω and v'=Rω'
From (b) to (c), forward slip will take place and backward maximum friction will convert it into pure rolling.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective32videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason11videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:View Solution
Knowledge Check
- Question 1 - Select One or More
A cylinder rolls without slipping on a rough floor, moving with a spped v. It makes an elastic collision with smooth vertical wall. After impact
Ait will with a speed v initiallyBits motion will be rolling without slippingCits motion will be rolling without slipping initially and its rotational motion will stop momentarily at some intantDits motion will be rolling without slipping only after some time - Question 2 - Select One
A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative
 AThe acceleration of the centre of the sphere is 9.8m/s2BThe acceleration of the centre of the sphere is 10m/s2CThe direction of frictional force on the sphere is towards rightDThe value of frictional force is 3N
AThe acceleration of the centre of the sphere is 9.8m/s2BThe acceleration of the centre of the sphere is 10m/s2CThe direction of frictional force on the sphere is towards rightDThe value of frictional force is 3N - Question 3 - Select One
A solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.
A ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor with velocity v0=10ms−1 towards a smooth vertical wall if coefficient of restitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
Linear velocity of first sphere after it again starts rolling without slipping isView SolutionWhen a hollow sphere is rolling without slipping on a rough horizontal surface then the percentage of its total K.E. which is translational is
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution

