
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0. Change in the rotational kinetic energy of the system is
K0/2
−K0/2
−K0/4
K0/4
The correct Answer is:A
K=L22I or K∝1I As I has doubled, so K will become half.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective32videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason11videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Rotational Kinetic Energy || Examples
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity ω1. Disk 2 rotating with the angular velocity ω2 is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I1andI2, respectively. The constant surface of the disks are rough.
View Solution
Knowledge Check
- Question 1 - Select One
The rotational kinetic energy is -
Amω2B12Iα2C12Iω2D12mv2 - Question 2 - Select One
Rotational kinetic energy is equal to
A1w2BI2w2C32Iw2D12Iw2 - Question 3 - Select One
The body is rotating with uniform angular velocity (ω ) having rotational kinetic energy ( E) . Its angular momentum (L ) is :
A2EωBE2ωCEω2DE2ω
Three particles are situated on a light and rigid rod placed along Y-axis. If the system rotates about X-axis, the M.I. of the system is :
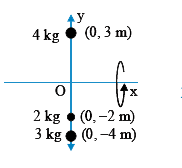 View Solution
View SolutionA disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
View SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionWhat is the ratio of the rolling kinetic energy and rotational kinetic energy in the motion of a disc ?
View SolutionA disc is rolling without slipping. The ratio of its rotational kinetic energy and translational kinetic energy would be -
View Solution

