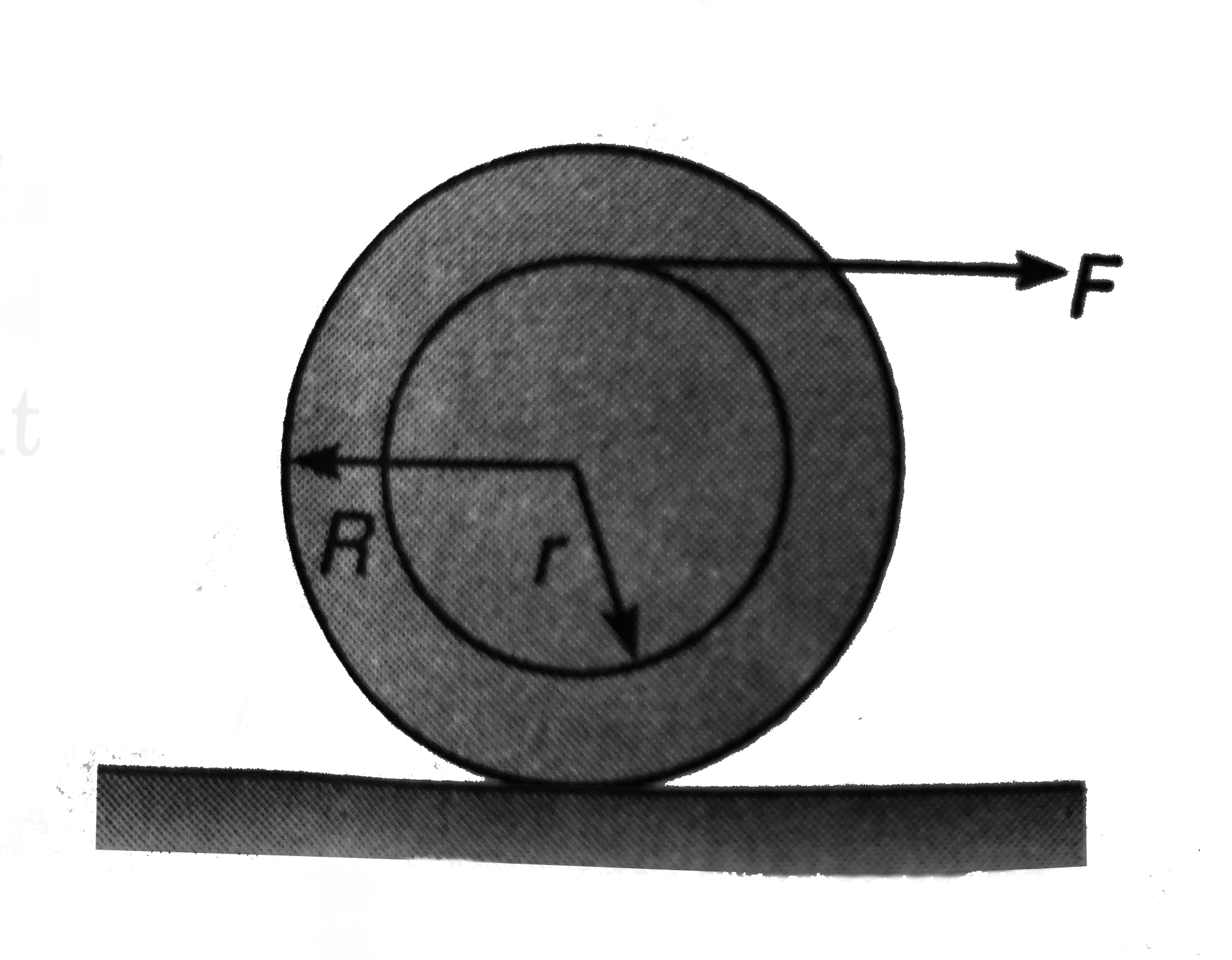
A heavy homogeneous cyliner has mass m and radius R. It is accelerated by a force F which is applied through a rope wound around a light drum of radius r attached to the cylinder (figure) the coefficient of static friction is sufficient for the cylinder to roll without slipping.
Find the friction force.
Find the acceleration a of the centre of the cylinder
it is possible to choose r, so that a is greater than Fm ? How ?
What is the direction of the friction in the circumstances of part(C)?

(a). For pure rolling to take place,
a=Rα or F−fm+R⎡⎣Fr+fR12mR2⎤⎦
Solving this equation we get
f=23(12−rR)
(b). Acceleration a=F−fm
substituting value of f from part (a), we get
a=2F3mR(R+r)
(c). a>Fm if 23R(R+r)>1 or r>R2
(d). In this case force of friction is in forward direction.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 21videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
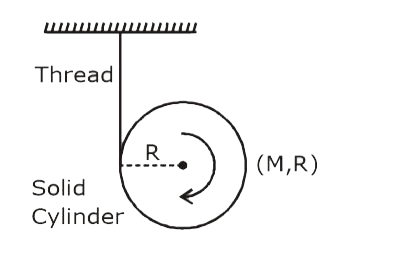
Thread would around cylinder of mass M and radius R. It is allowed to fall as shown. Find its acceleration.
 View Solution
View SolutionA horizontal force P applied at a height h above the centre of a solid cylinder of mass M, radius R. Determine force of friction in terms of h show that friction force is zero for h=R/2. Assume that the cylinder rolls without slipping.
View Solution
Knowledge Check
- Question 1 - Select One

A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?AF/4BF/3CF/2D2F/3 - Question 2 - Select One
A uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
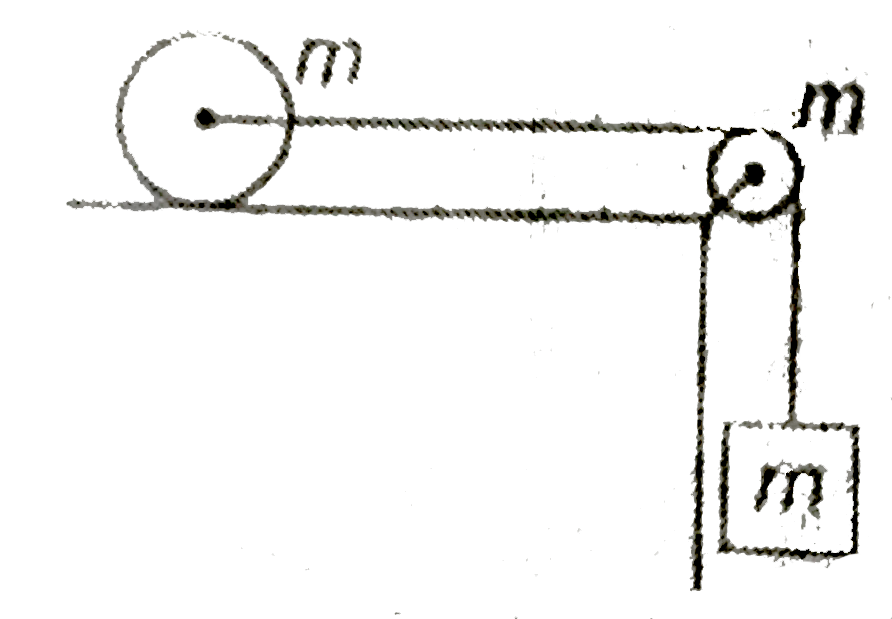
Force of friction acting on the cylinder isA2mg3B3mg2Cmg3Dmg6 - Question 3 - Select One
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZero
A uniform solid cylinder of mass M and radius 2R rests on a horizontal table top. A string attached to it runs over a pulley (disc) of mass M and radius R thatis mounted on a frictionless axle through its centre. A block of mass M is suspended from the free end of the string. The string doesn't slip over the pulley surface, and the cylinder rolls without slipping on the, table top. Find the acceleration of the block.

[g/3]View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
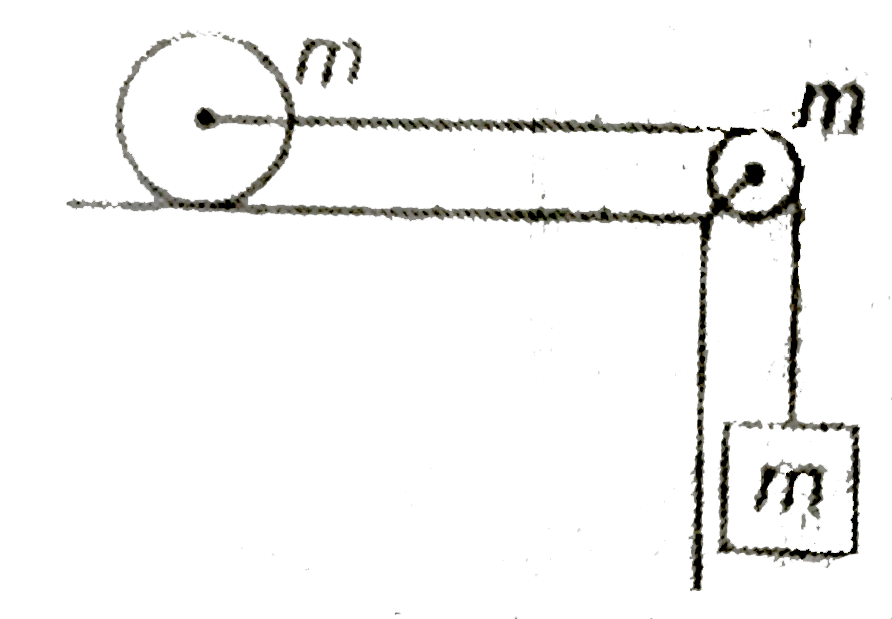
Angular acceleration of the cylinder isView SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
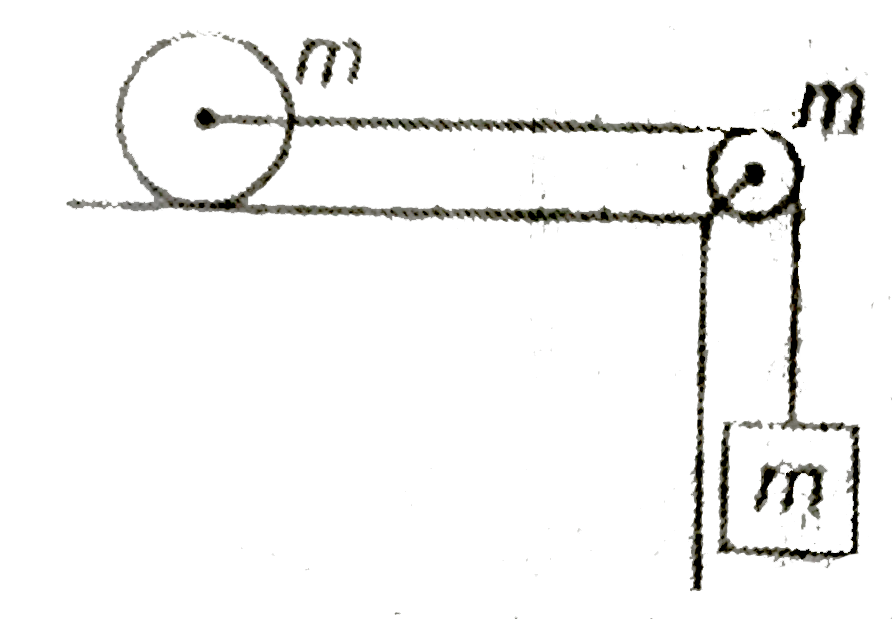
Acceleration of the block isView SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
View Solution

