Two uniform cylinders, each of mass m=10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine
the tension in the portion of the belt connecting the two cylinders.
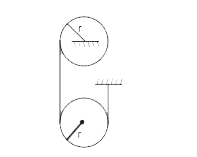
The correct Answer is:2007N
Step by step video & image solution for Two uniform cylinders, each of mass m = 10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine the tension in the portion of the belt connecting the two cylinders. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - I)
24 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - II)
49 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 3 (Level - I)
27 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 4 (LEVEL - II)
14 Videos
Similar Questions
Two uniform cylinders, each of mass m=10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine
the velocity of the centre of cylinder A after it has moved through 1.2 m &
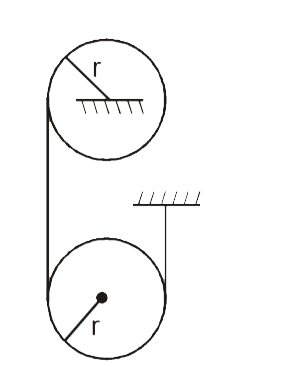
View SolutionTwo uniform solid cylinders, each of mass m = 10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine the velocity of the centre of cylinder A after it has moved through 1.2 m & the tension in the portion of the belt connecting the two cylinders.
View Solution
Knowledge Check
A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
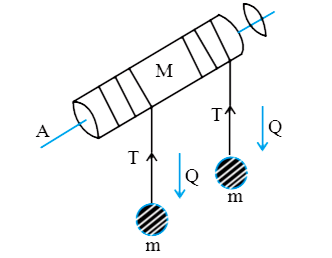 AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4m
AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4mA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3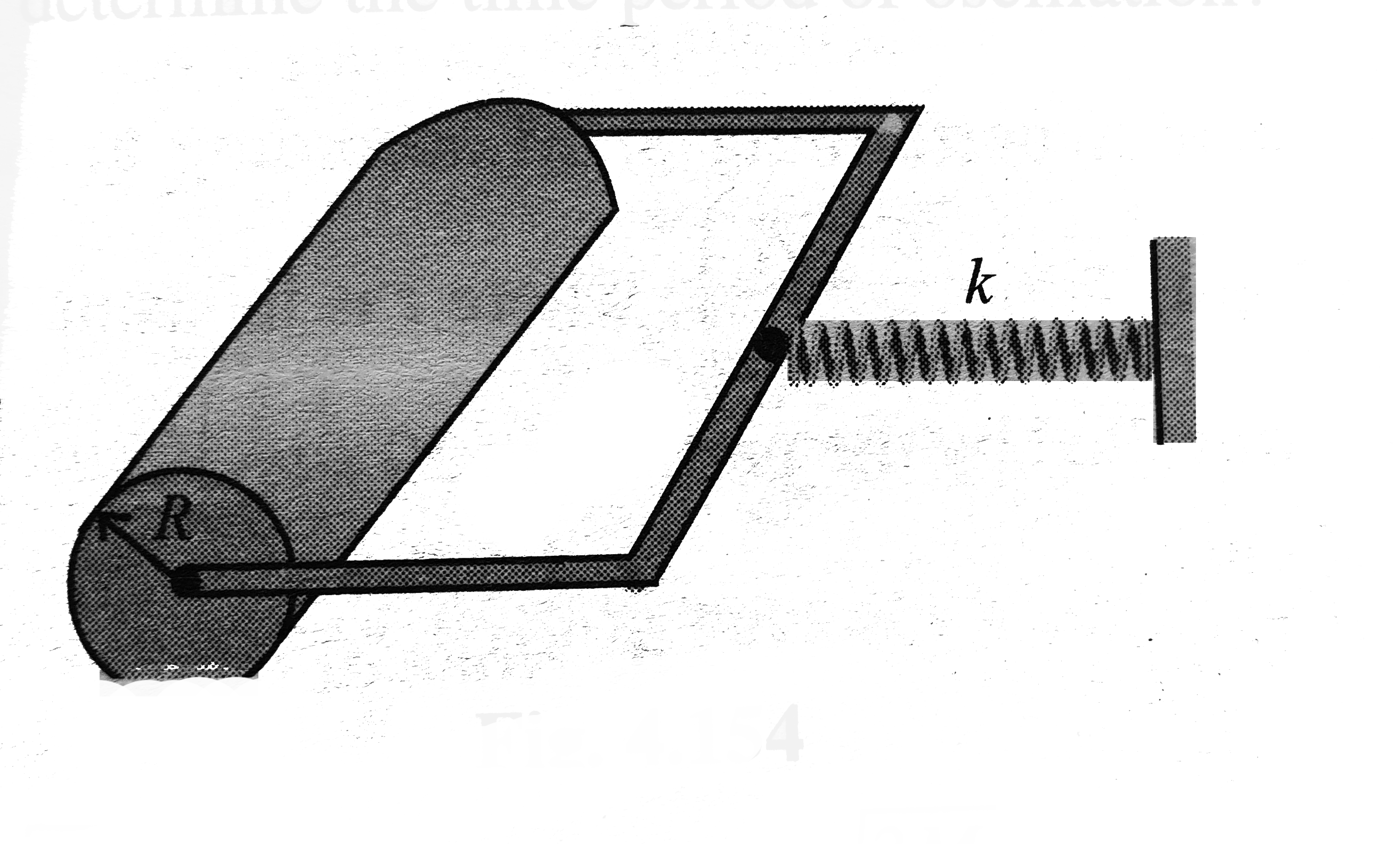
A soil cylinder of mass M and radius R is connected to a spring as shown in fig. The cylinder is placed on a rough horizontal surface. All the parts except the cylinder shown in the figure are light. If the cylinder is displaced slightly from its mean position and released, so that it performs pure rolling back and forth about its equilibrium position, determine the time period of oscillation?A2π√MkB2π√3M2kC2π√3MkDnone of these
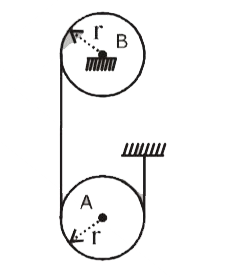
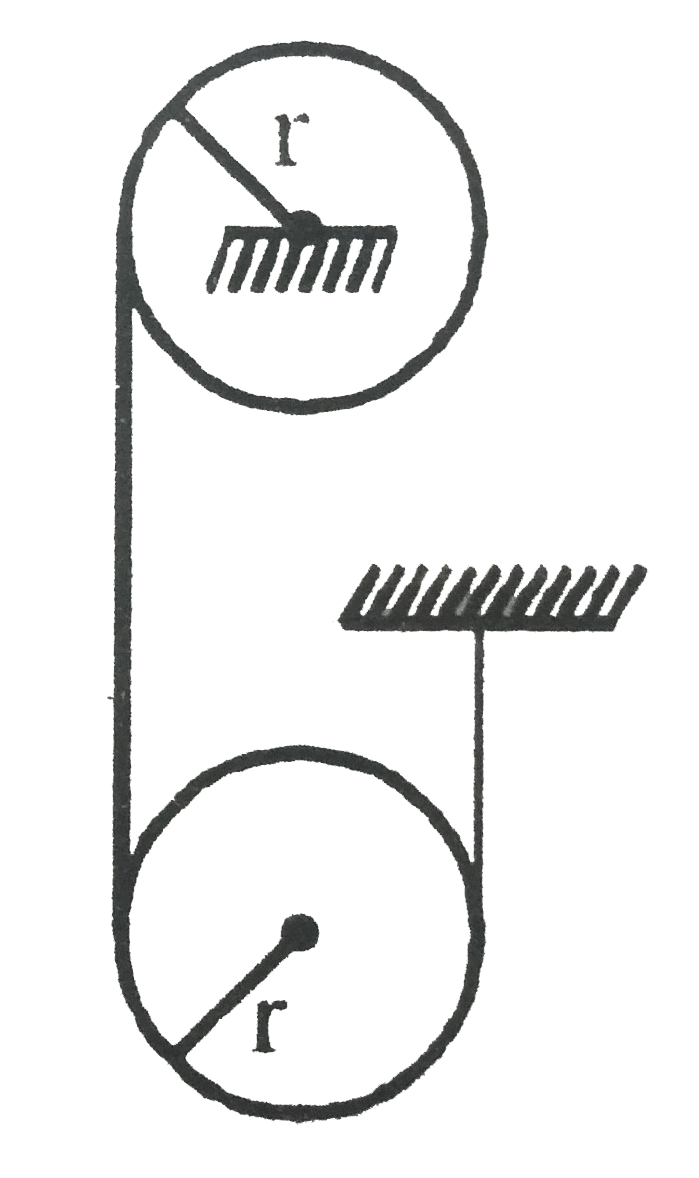
Two uniform cylinders, each if mass m=10kg and radius r=150mm, are connected by a rought belt as shown. If the system is released from rest. Determine.
(a) the velocity of the centre of cylider A after it has moved through 1.2m and
(b) the tension in the portion of the belt connecting the two cylinders.
 .
.
View SolutionConsider the system shown in fig. the system os released from rest, find the tension in the cord connected between 1kg and 2 kg blocks.

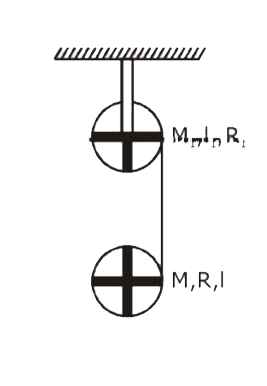
View SolutionA string is would over a cylinder of mass M, radius R and moment of inertia I and then the string is would over the pulley as shown in the figure. If the system is released from rest then determine the tension is tring. Assume there is no slipping between string and pulley cylinder.
View SolutionTwo bodies of masses 2kg and 3kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string (g=10ms−2)
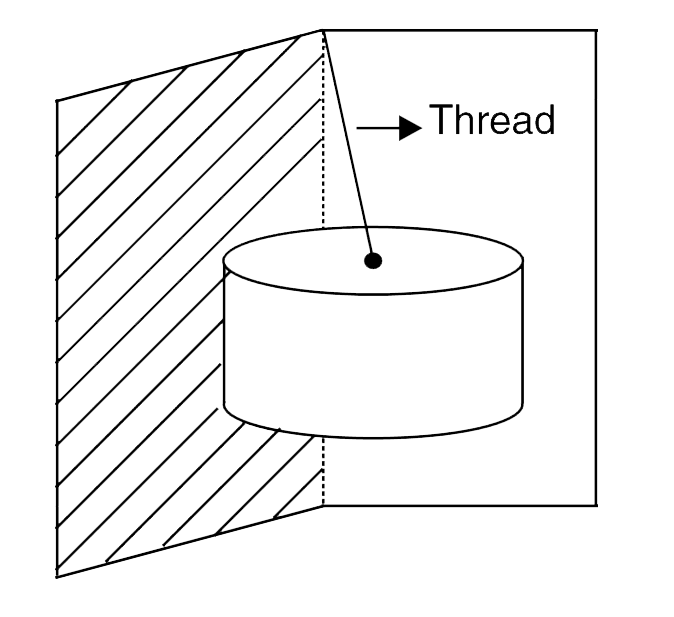
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
View Solution
