Six particles each of mass 'm' are placed at six verties A,B,C,D,Eand F of a regular hexagon of side 'a'. A seventh particle of mass 'M' is kept at center 'O' of the hexagon.
(a)Find net force on 'M'.
(b)Find net force on 'M' if particles at A is removed.
(c) Find net force on 'M' if particles at A and C are removed .
The correct Answer is:A, B, D
(a) FA=FB=FD=FE=FF=GmMa2=F (say)
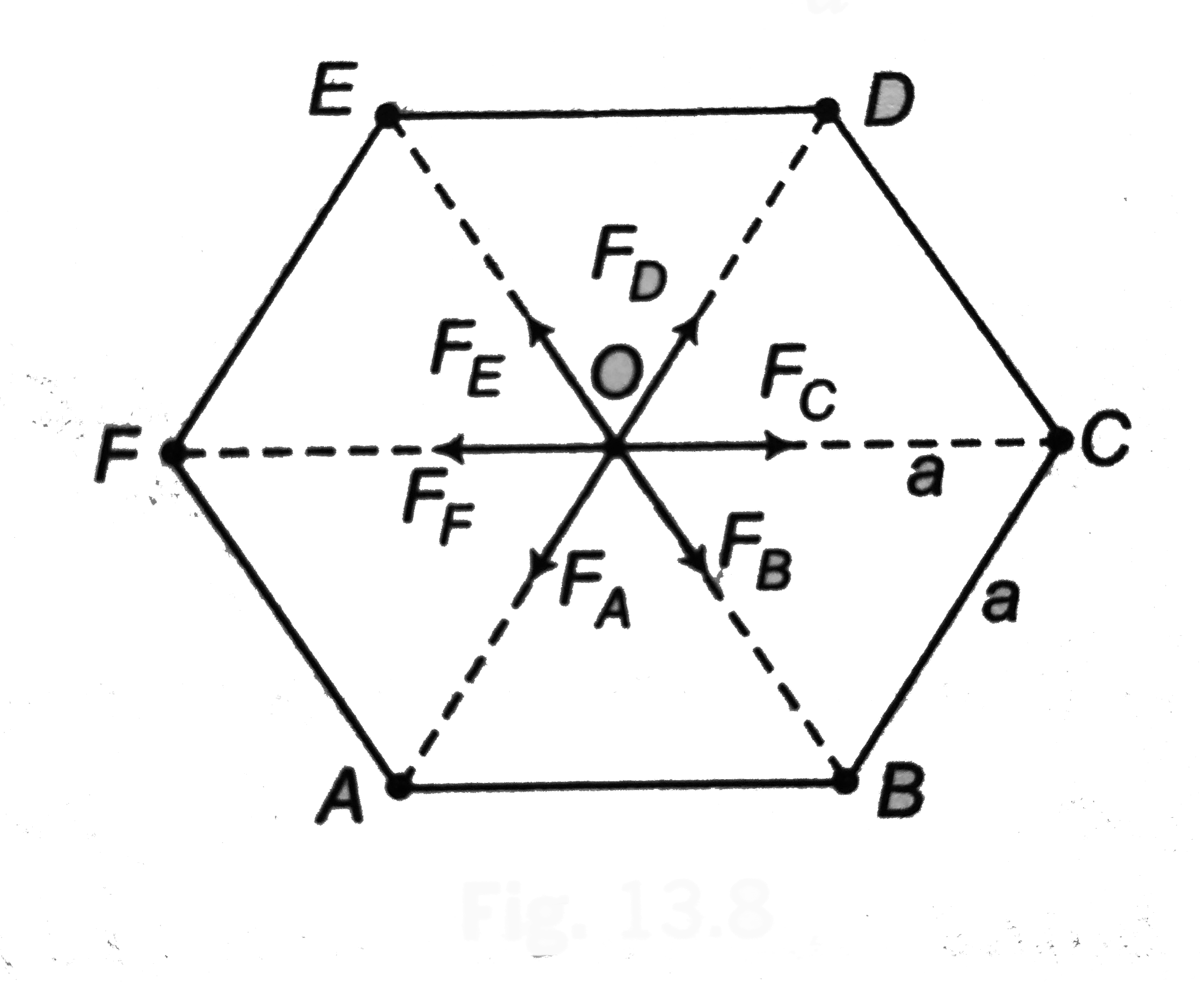
So, net force will be zero, as three pairs of equal and opposite forces are acting on 'M' at O.
(b) When paricles at A is removed then FA is removed . So, there is no force to cancel FD.
∴Fnet=FD=GMma2 (towards D)
(c) When particles at A and C are removed then, FA and FC are removed.FB and FB and FE are still cancelled. So, net force is the resultant of two forces FD and FF of equal magnitudes acting at 120∘. So, the resultant will pass through the centre ot towards E. magnitude of this resultant is
Fnet=√F2+F2+2(F)(F)cos120∘
=F=GMma2 (towards E)
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Solved Examples
Explore 16 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Miscellaneous Examples
Explore 8 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
Five particles each of mass 'm' are kept at five verties of a regular pentagon . A sixth particles of mass 'M' is kept at center of the pentagon 'O'.Distance between'M' and is 'm' is 'a'. Find
(a) net force on 'M'
(b) magnitude of net force on 'M' if any one particle is removed from one of the verties.
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View Solution
Knowledge Check
Six particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
A6Gm2a2B6Gmm0a2CzeroD6Gma4Three particles each of mass m are placed at the three corners of an equilateral triangle of side L. A particle of mass M is kept at the midpoint of any one side. What is the force acting on M, due to this system of 3 particles ?
AGMm4L2B34GMmL2C43GMmL2D4GMmL2Six s imilar magnetic poles are placed on six corners of a regular hexagon of side 10cm. A south pole of strength 10Am is placed at the centre of hexagon. Find the magnetic force on the south pole.
AZeroB4π×10−4NC10 NDNone of these
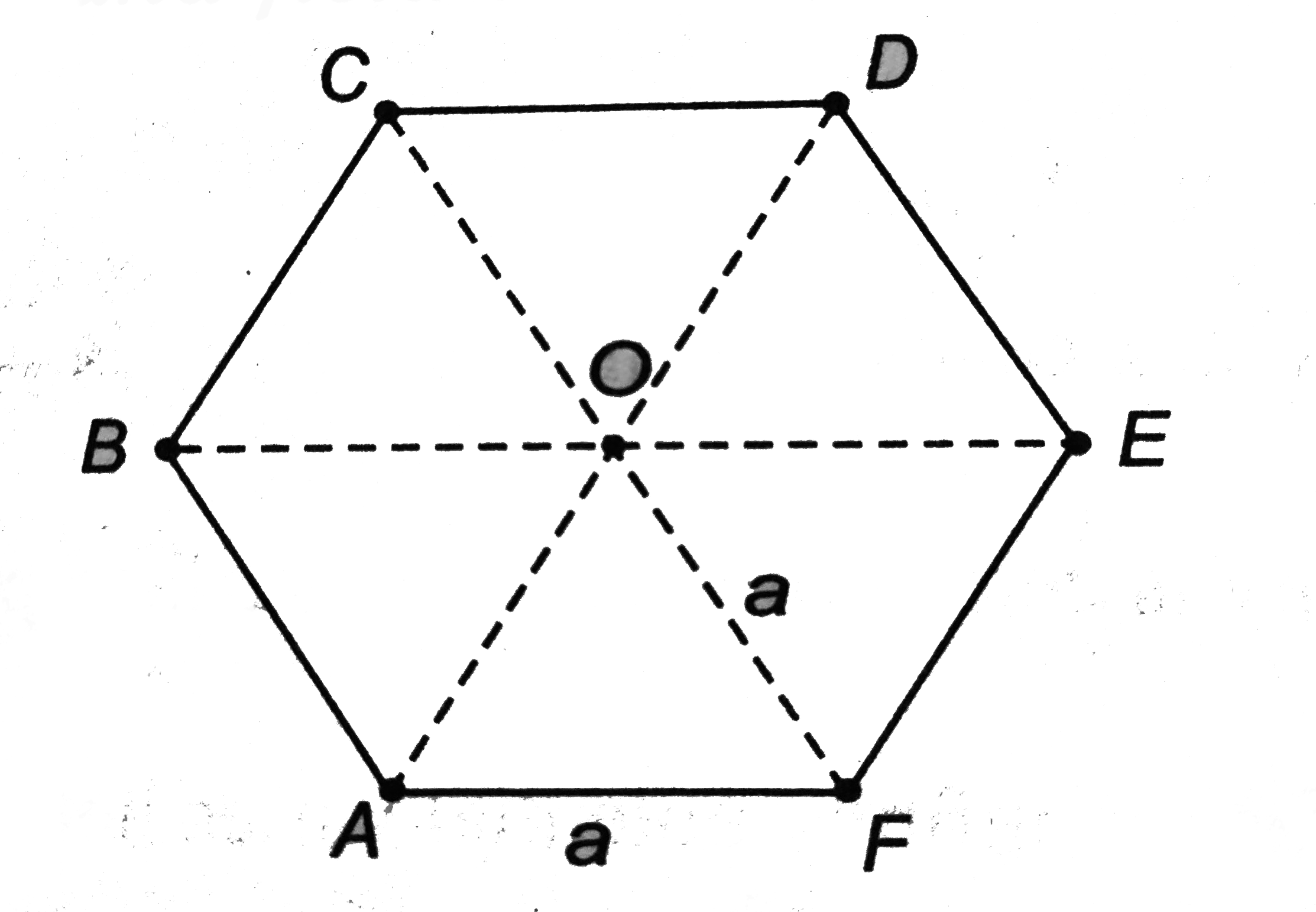
Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
 .
.
View SolutionEight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
 .
.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionIf two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View Solution