Identify the correct variation of potential energy U as a function of displacement x from mean position (or x2) of a harmonic oscillator (U at mean position =0)


None of these
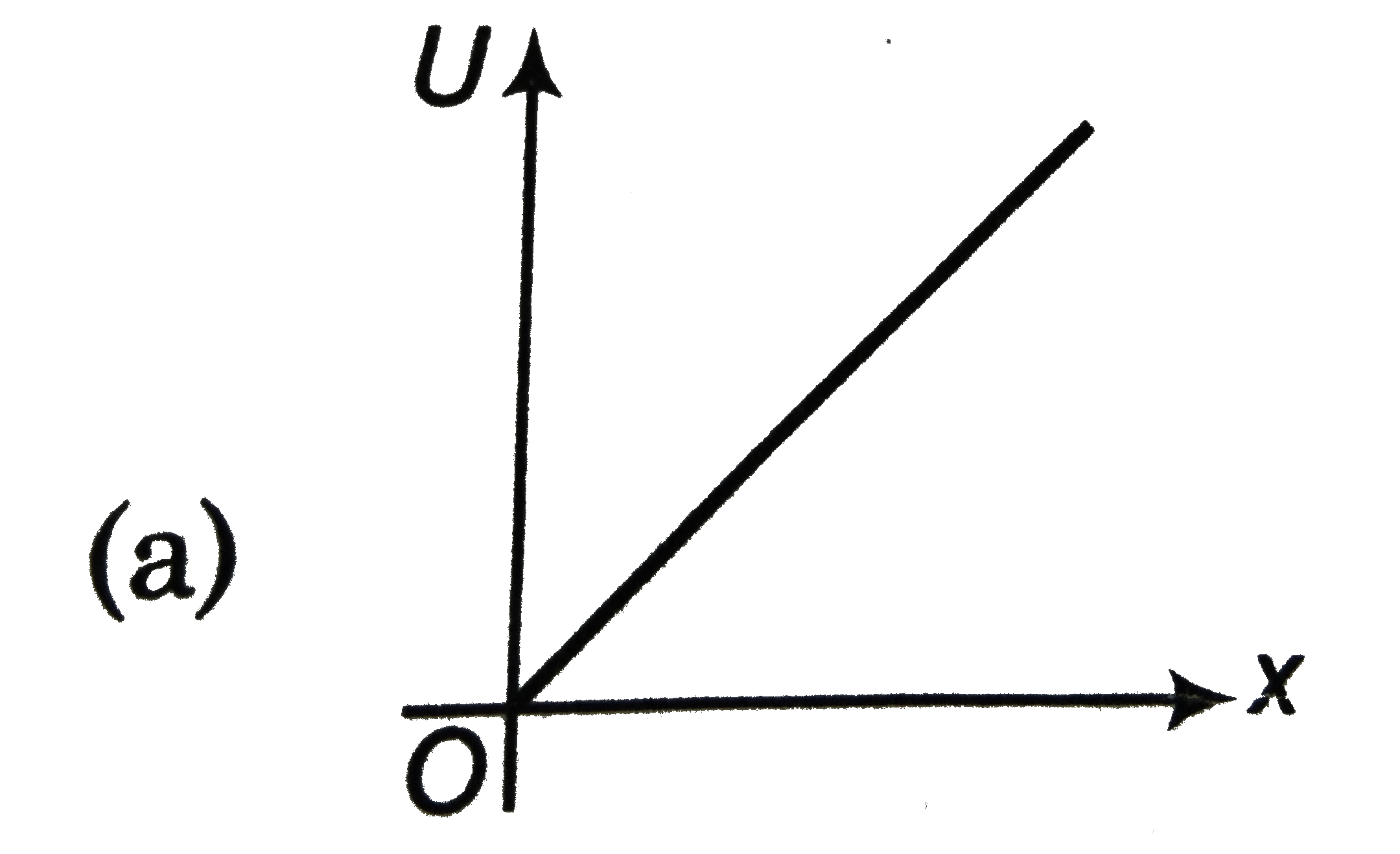
The correct Answer is:C
U=12kx2
i.e. U versus x2 graph is a straight line passing through origin.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective39videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct28videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason10videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
Similar Questions
Acceleration of a particle in SHM at displacement x=10cm (from the mean position is a=−2.5cm/s2). Find time period of oscillations.
View SolutionA particle executes simple harmonic motion of ampliltude A. At what distance from the mean position is its kinetic energy equal to its potential energy?
View Solution
Knowledge Check
- Question 1 - Select One
In a simple harmonic oscillator, at the mean position
A(a) kinetic energy is minimum, potential energy is maximum.B(b) both kinetic and potential energies are maximum.C(c ) kinetic energy is maximum, potential energy is minimum.D(d) both kinetic and potenteal energies are minimum. - Question 2 - Select One
In. a simple harmonic oscillator, at the mean position
Akinetic energy Is minimum potential energy Is maximumBBoth kinetic and potential energy are maximumCkinetic energy Is maximum, potential energy Is minimumDBoth kinetic and potential energies are minimum - Question 3 - Select One
The velocity of a particle in simple harmonic motion at displacement y from mean position is
Aω√a2+y2Bω√a2−y2CωyDω2√a2−y2
At which position the potential energy of a harmonic oscillator is maximum or minimum ?
View SolutionThe potential energy as a function of displacement for an oscillator u=8x2 joule. The magnitude of the force on the oscillator of mass 0.5 kg placed at x = 0.2 m is
View SolutionA body is executing simple harmonic motion. At a displacement x from mean position, its potential energy is E1=2J and at a displacement y from mean position, its potential energy is E2=8J. The potential energy E at a displacement (x+y) from mean position is
View SolutionThe potential energy of a particle with displacement X is U(X). The motion is simple harmonic, when (K is a positive constant)
View SolutionThe graph between potential energy U and displacement X in the state of stable equilibrium will be–
View Solution
