The potential energy as a function of displacement for an oscillator joule. The magnitude of the force on the oscillator of mass 0.5 kg placed at x = 0.2 m is
1.6 N
3.2 N
0.8 N
4.8 N
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
The gravitational potential in a region is given by, V=200(X+Y)J/kg. Find the magnitude of the gravitational force on a particle of mass 0.5kg placed at the orgin.
View SolutionThe potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View Solution
Knowledge Check
Identify the correct variation of potential energy U as a function of displacement x from mean position (or x2) of a harmonic oscillator (U at mean position =0)
A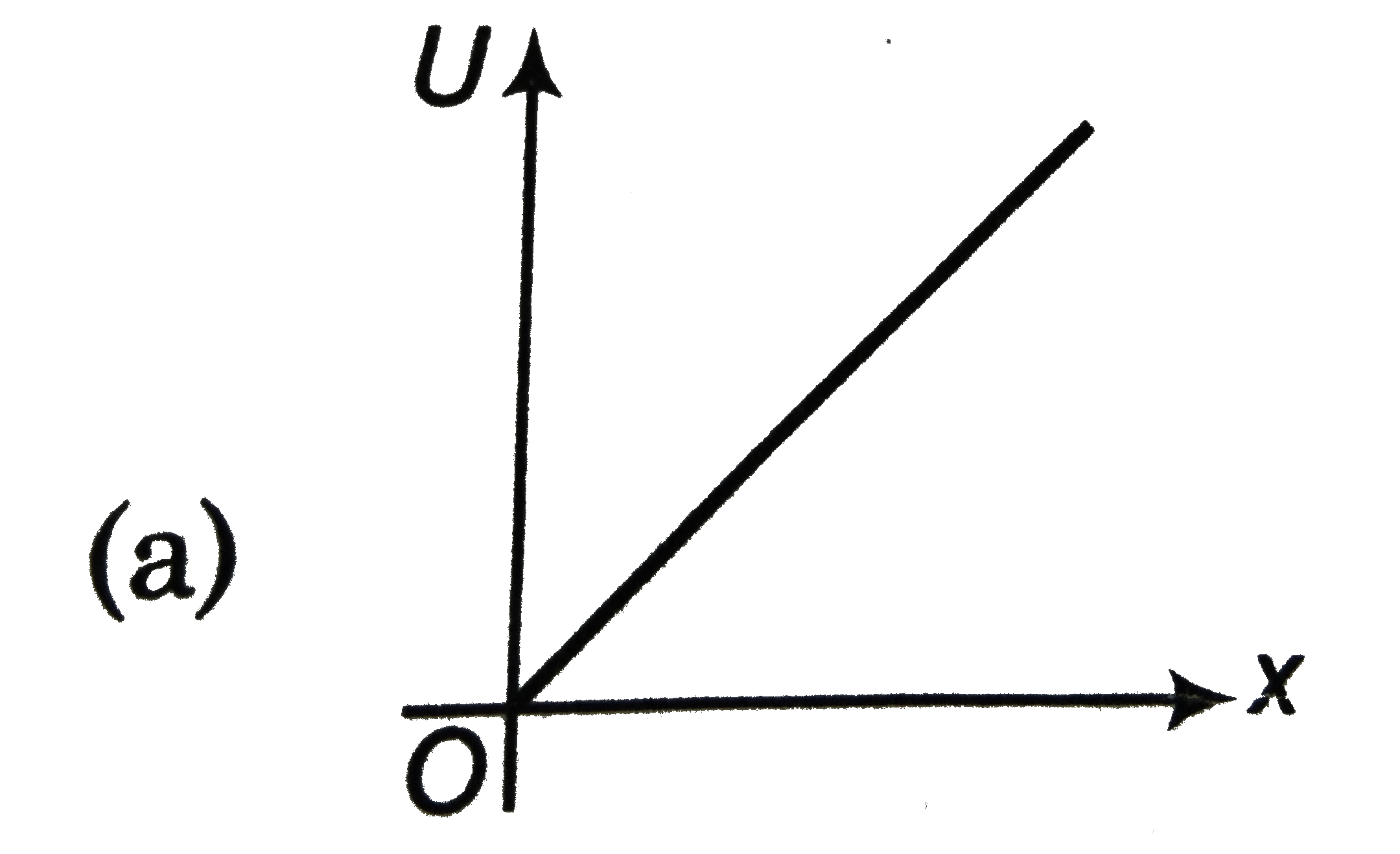 B
B C
C DNone of these
DNone of theseThe potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
A1B√2C1√2D0If the potential energy of an oscillator is U=a+bx+cx2+dx3, the term (quantity) which indicates the SHM of the oscillator is
AaBbxCcx2Ddx3
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
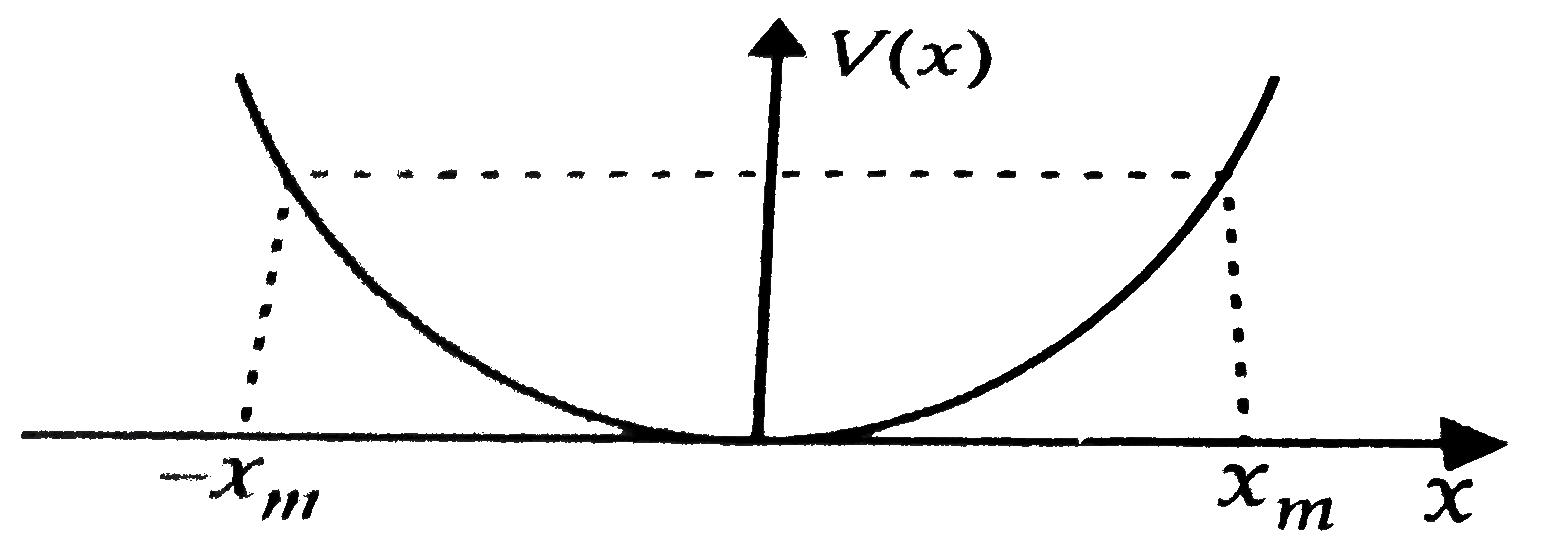
View SolutionThe potential energy of a particle oscillating on x-axis is given as U+20+(x−2)2. The mean position is at
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for

View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
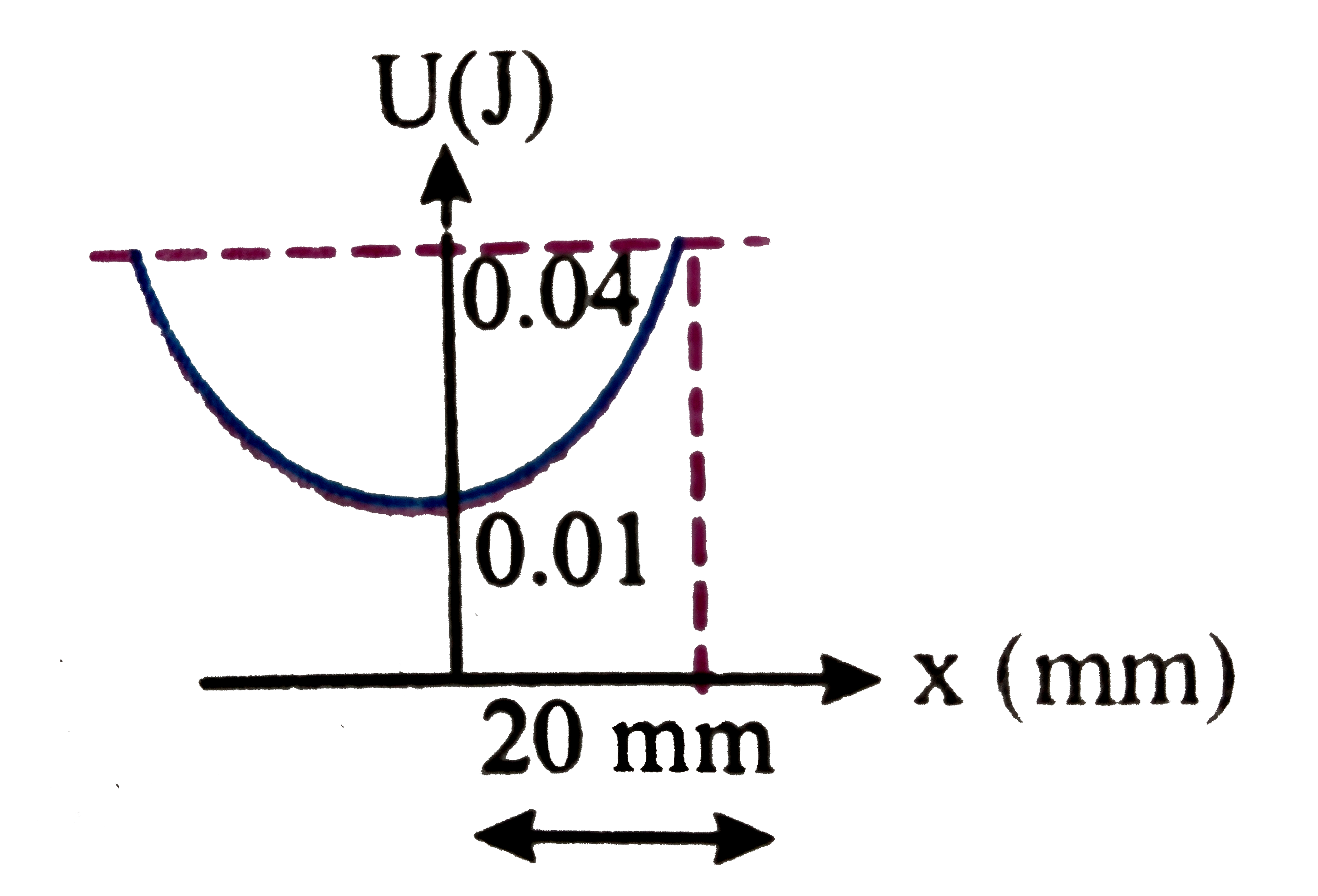
View SolutionThe potential energy of a particle executing SHM along the x-axis is given by U=U0−U0cosax. What is the period of oscillation?
View Solution
