In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

The correct Answer is:A, B, C, D
When the mass m is displaced from its mean position by a distance x, let F be the restoring (extra tension) force produced in the string. By this extra tension further elongation in the springs are
2Fk1 , 2Fk2, 2Fk3 and 2Fk4 respectively.
Then,
x=2(2Fk2)+2(2Fk2)+2(2Fk3)+2(2Fk4)
or F(4k1+4k2+4k3+4k4)=−x
Here negative sign shows the restoring nature of force.
a=−xm(4k1+4k2+4k3+4k4)
T=2π√∣∣xa∣∣
=4π√m(1k1+1k2+1k3+1k4)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.15videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.1videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension2videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
Similar Questions
In the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
 View Solution
View Solution
In the arrangement shown if Fig. Pulleys are small and light and spring are ideal and K1=25(π2)Nm, K2=2K1,K3= and K4=4K1 are the force constant of the spring. Calculate the period of small vertical oscillation of block of mass m=3kg.View Solution
Knowledge Check
- Question 1 - Select One
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
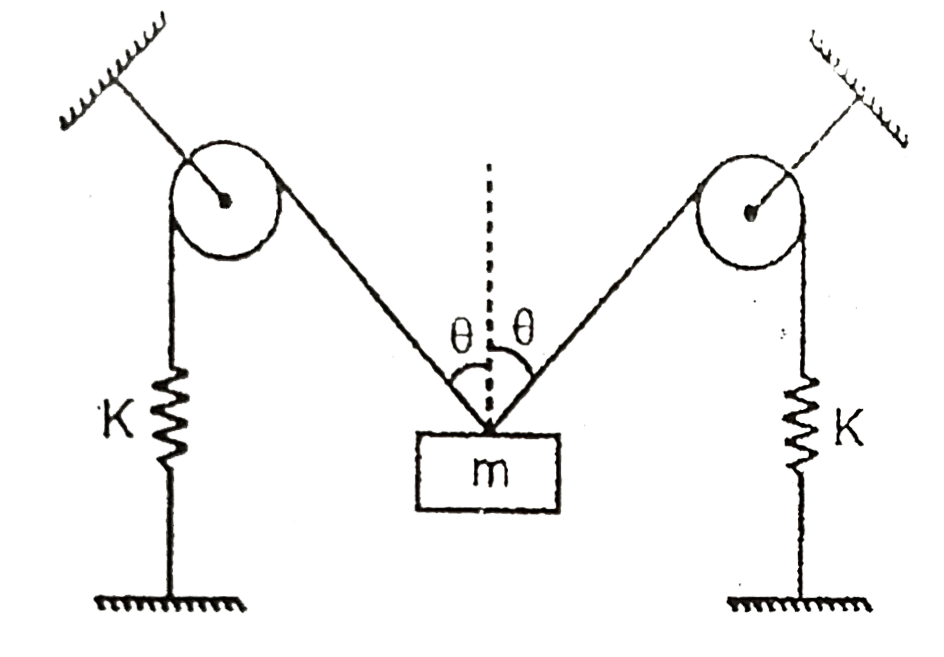 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k - Question 2 - Select One
As shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
 Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2
Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.
 View Solution
View SolutionThere is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
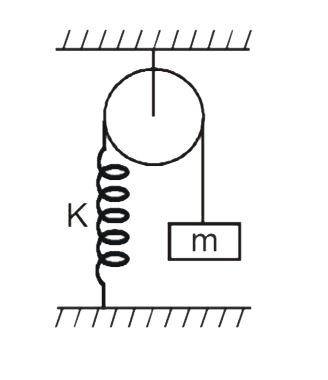 View Solution
View SolutionAs shown in the figure a block of mass m is hung from the ceiling by the system of springs consisting of two layers. The force constant of each of the springs is k. The frequency of the vertical oscillations of the block is
View SolutionTwo light springs of force constants (k_1 and k_2) and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block k1=1.8N/m,k2=3.2N/m,m=200gm).
(##JMA_CHMO_C10_026_Q01##).View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is
 View Solution
View Solution

