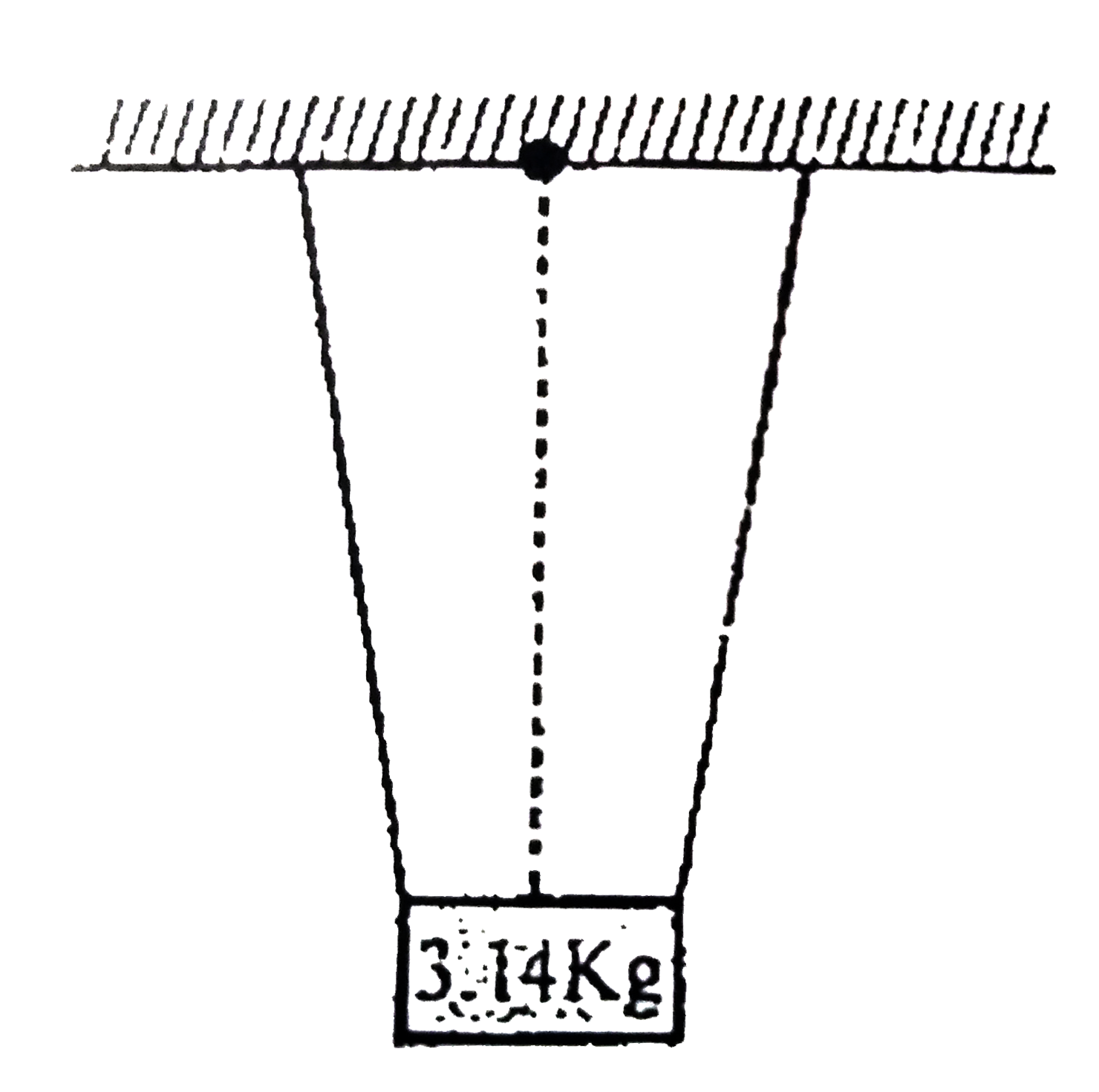
A body of mass 3.14kg is suspended from one end of a wire of length 10m. The radius of cross-section of the wire is changing uniformly from 5×10−4m at the top (i.e. point of suspension) to 9.8×10−4m at the bottom . Young's modulus of elasticity is 2×1011N/m2. The change in length of the wire is

A

4×10−3m

B

3×10−3m

C

10−3m

D

2×10−3m

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Change in length of element is
Cross-sectional area of the element is
A=π[a+b−aLx]2
Where , a=b−aLx is radius of the wire at the location of element .
d(Δl)=Fπ[a+b−aLx]2Ydx
Total change in length of wire is
Δl=FπY∫Lo1(a+b−aLx)2dx
Let a+b−aLx=t
⇒b−aLdx=dt⇒dx=Lb−adt
When x=o , t=a and when x=L,t=b
∴Δl=FπY∫bat−2.Lb−adt
=FLπY(b−a)(−1)(1b−1a)
=FLπY(b−a).b−aab=FLπYab
=(3.14)(9.8)(10)(3.14)(2×1011)(5×10−4)(9.8×10−4)
=10−3m⇒∴ΔL=10−3m
ocr_image

Updated on:21/07/2023
|
Class 11PHYSICSPROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A body of mass 6.28 kg is suspended from one end of a wire of length 10 m. The radius of the wire is changing uniformly from 19.6×10−4m at one end to 10×10−4m at the order end. Find the change in the length of the wire.
    [Y=2×1011N/m2]

    A0.1 mm
    B0.3 mm
    C0.5 mm
    D0.7 mm

  • A wire of area of cross section 1×10−6m2 and length 2 m is stretched through 0.1×10−3m. If the Young's modulus of a wire is 2×1011N/m2, then the work done to stretch the wire will be

    A0.05×10−4J
    B0.5×10−4J
    C5×10−4J
    D50×10−4J

  • An iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is

    A0.2 mm
    B0.5 mm
    C2 mm
    D1 mm