A solid sphere of radius R made of a material of bulk modulus B is surrounded by a liquid in a cylindrical container. A massless piston of area A (the area of container is also A) floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid , fractional change in radius of the sphere is MgαAB. Find the value of α.
The correct Answer is:C
To solve the problem, we need to find the value of α in the fractional change in radius of a solid sphere when a mass is placed on a piston floating on the surface of a liquid. The steps to derive the solution are as follows:
Step 1: Understand the setup
We have a solid sphere of radius R surrounded by a liquid in a cylindrical container. A massless piston of area A floats on the surface of the liquid. When a mass M is placed on the piston, it compresses the liquid, leading to a change in pressure.
Step 2: Calculate the change in pressure
The pressure change ΔP due to the mass M placed on the piston can be calculated using the formula:
ΔP=MgA
where g is the acceleration due to gravity.
Step 3: Relate pressure change to volume change
Using the definition of bulk modulus B:
B=−ΔPΔVV
we can rearrange this to find the change in volume:
ΔVV=−ΔPB
Substituting for ΔP:
ΔVV=−Mg/AB
Step 4: Express the volume of the sphere
The volume V of the sphere is given by:
V=43πR3
Thus, the change in volume ΔV can also be expressed in terms of the change in radius ΔR:
ΔV=V′−V=43π(R+ΔR)3−43πR3
Using the binomial expansion for small changes, we can approximate:
ΔV≈4πR2ΔR
Step 5: Substitute into the bulk modulus equation
Now we can substitute ΔV into the bulk modulus equation:
4πR2ΔR43πR3=−Mg/AB
Simplifying gives:
3ΔRR=−3Mg4AB
Step 6: Solve for the fractional change in radius
From the equation above, we can express the fractional change in radius:
ΔRR=−Mg4AB
This indicates that the fractional change in radius is:
ΔRR=−Mg4AB
Step 7: Identify the value of α
Comparing this with the given expression for fractional change in radius:
ΔRR=MgαAB
we can see that:
α=4
Final Answer
Thus, the value of α is:
α=4
We have a solid sphere of radius R surrounded by a liquid in a cylindrical container. A massless piston of area A floats on the surface of the liquid. When a mass M is placed on the piston, it compresses the liquid, leading to a change in pressure.
The pressure change ΔP due to the mass M placed on the piston can be calculated using the formula:
ΔP=MgA
where g is the acceleration due to gravity.
Using the definition of bulk modulus B:
B=−ΔPΔVV
we can rearrange this to find the change in volume:
ΔVV=−ΔPB
Substituting for ΔP:
ΔVV=−Mg/AB
The volume V of the sphere is given by:
V=43πR3
Thus, the change in volume ΔV can also be expressed in terms of the change in radius ΔR:
ΔV=V′−V=43π(R+ΔR)3−43πR3
Using the binomial expansion for small changes, we can approximate:
ΔV≈4πR2ΔR
Now we can substitute ΔV into the bulk modulus equation:
4πR2ΔR43πR3=−Mg/AB
Simplifying gives:
3ΔRR=−3Mg4AB
From the equation above, we can express the fractional change in radius:
ΔRR=−Mg4AB
This indicates that the fractional change in radius is:
ΔRR=−Mg4AB
Comparing this with the given expression for fractional change in radius:
ΔRR=MgαAB
we can see that:
α=4
Thus, the value of α is:
α=4
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Example39videos
ELASTICITY
- BOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.115videos
ELASTICITY
- BOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 Comprehension Based6videos
ELASTICITY
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions434videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
A solid sphere of radius R made of a material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless pistion of area A floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid the fractional change in the radius of the sphere, δR/R, is .............
View SolutionRadius of a sphere is 14 cm. Find the surface area of the sphere.
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of radius R made of a material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless pistion of area A floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid the fractional change in the radius of the sphere, δR/R, is .............
Amg3KaBmgKaCKamgDKa3mg - Question 2 - Select One
A container filled with a liquid A is floating on the surface of another liquid 'B' as shown in the figure, then volume of the liquid displaced by the container
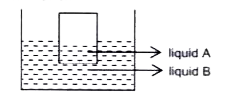 Ais equal to the weight of the liquid A.Bis greater than the weight of the liquid A.Cis less than the weight of the liquid ADCannot be determined
Ais equal to the weight of the liquid A.Bis greater than the weight of the liquid A.Cis less than the weight of the liquid ADCannot be determined - Question 3 - Select One
A container filled with a liquid A is floating on the surface of another liquid 'B' as shown in the figure, then volume of the liquid displaced by the container
 Ais equal to the volume of the liquid A.Bis greater than the volume of the liquid A.Cis less than the volume of the liquid A.DCannot be determined
Ais equal to the volume of the liquid A.Bis greater than the volume of the liquid A.Cis less than the volume of the liquid A.DCannot be determined
If the pin hole in the container is very small compared to the area of the base of container and a block floats in the ideal liquid then, the speed of efflux is
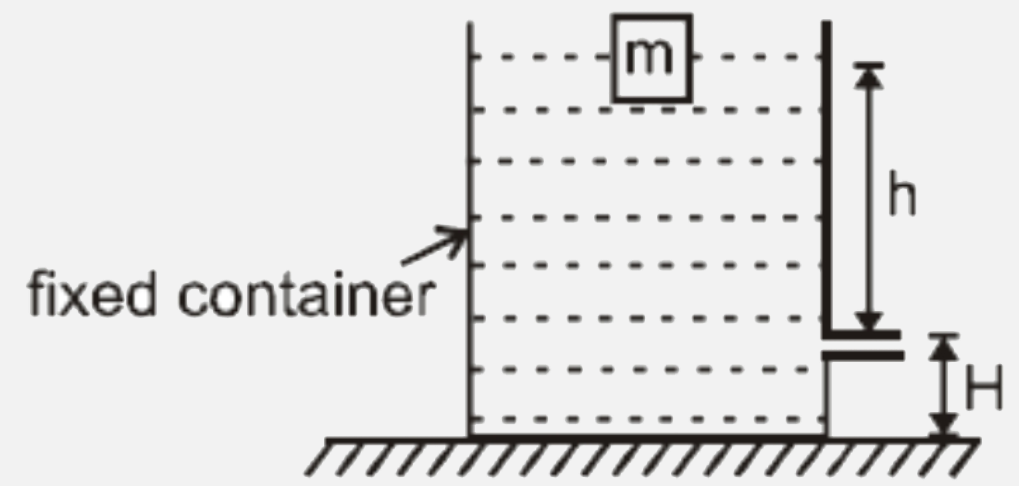 View Solution
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View SolutionThe bulk modulus for an incompresssible liquid is
View SolutionThe vapour pressure of a liquid in a closed container depends on:
(1) temperature of liquid (2) quantity of liquid (3) surface area of the liquidView Solution

