A U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury. Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with , determine the value of
 .
.
The correct Answer is:A, B, C

.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples21videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Length of a horizontal arm of U-tube is L and ends of both the vertical arms are open to atompsheric pressure P0, A liquid of density ρ is poured in the tube such that liquid just fills the horizontal part of the tube as shown in figure . Now one end of the opened ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0. if length of each vertical arm is a and in the sealed end liquid rises to a height y, find pressure in the sealed tube during rotation.
View SolutionAn open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
View Solution
Knowledge Check
- Question 1 - Select One
Fig, shows a U-tube of uniform cross-sectional area A accelerated with acceleration a as shown. If d is the seperation between the limbs. Then the difference in the levels of the liquid in the U−tube is
 AadgBgadCadgDad+g
AadgBgadCadgDad+g - Question 2 - Select One
A U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of 10mm above the water level on the other side. Meanwhile the water rises by 65mm from its original level (see diagram). The density of the oil is:
 A425kgm−3B800kgm−3C928kgm−3D650kgm−3
A425kgm−3B800kgm−3C928kgm−3D650kgm−3 - Question 3 - Select One
A U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of 10mm above the water level on the other side. Meanwhile the water rises by 65mm from its original level (see diagram). The density of the oil is:
 A425kgm−3B800kgm−3C928kgm−3D650kgm−3
A425kgm−3B800kgm−3C928kgm−3D650kgm−3
A tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
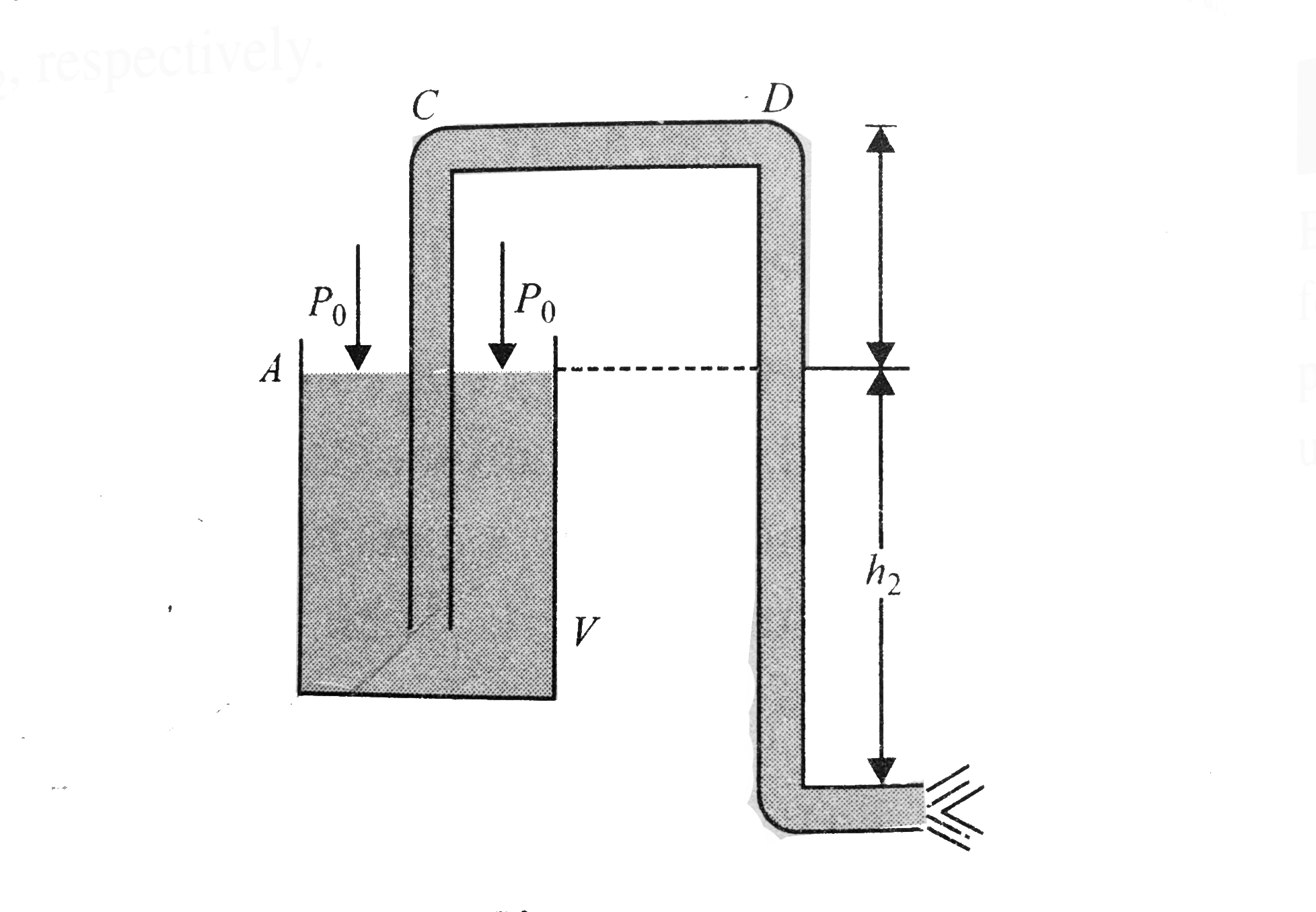
Given h1=h2=3.0m, the gauge pressure of water in the highest level CD of the tube will beView SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
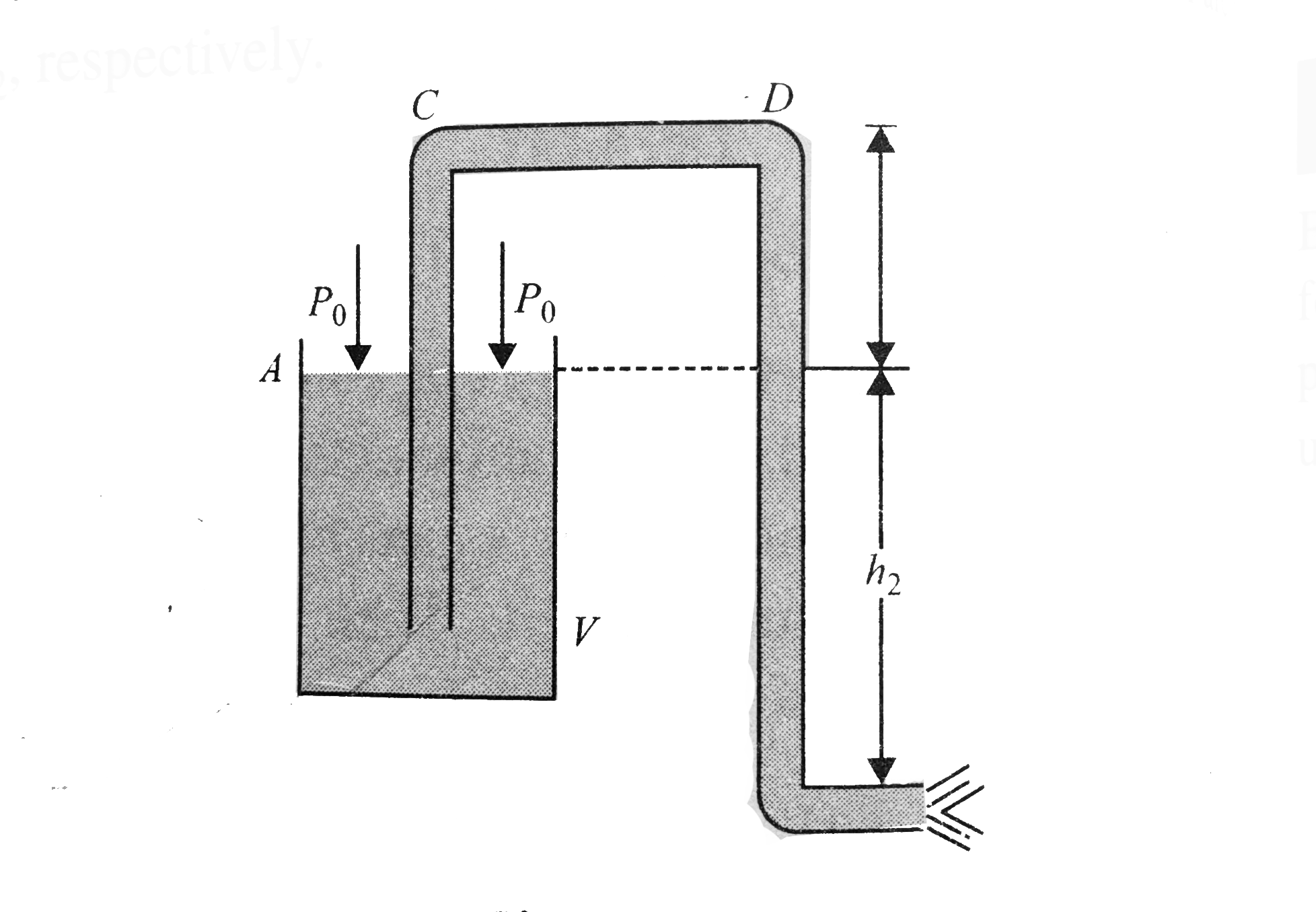
If h1=h2=3.0m, the maximum value of h1, for which the siphon will work will beView SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.

Determine the velocity vB of the water issuing out at B.View SolutionA U tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are at the same level with 10 cm of water in one arm and 12.5 cm of spirit in the other as shown in figure. The relative density of the spirit is
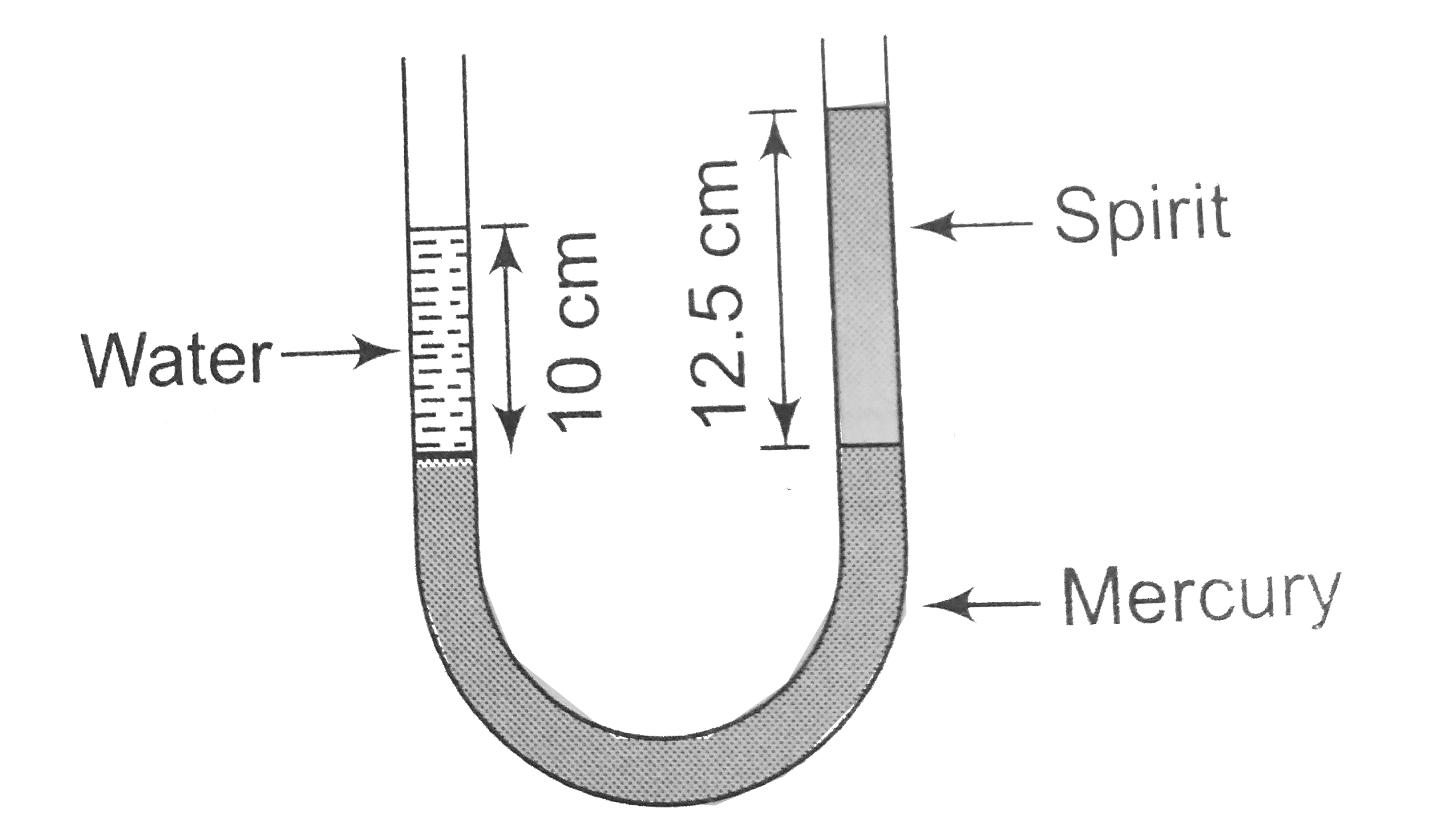 View Solution
View SolutionA U - tube having a horizontal arm of length 20 cm, has a uniform cross - sectional area 1cm2. It is filled with water of volume 60 cc. The volume of a liquid of density 4 g cc−1 required to be poured in one arm of the U - tube so that no water is left in the horizontal arm of the tube is (take g =9.8ms−2)
View Solution

