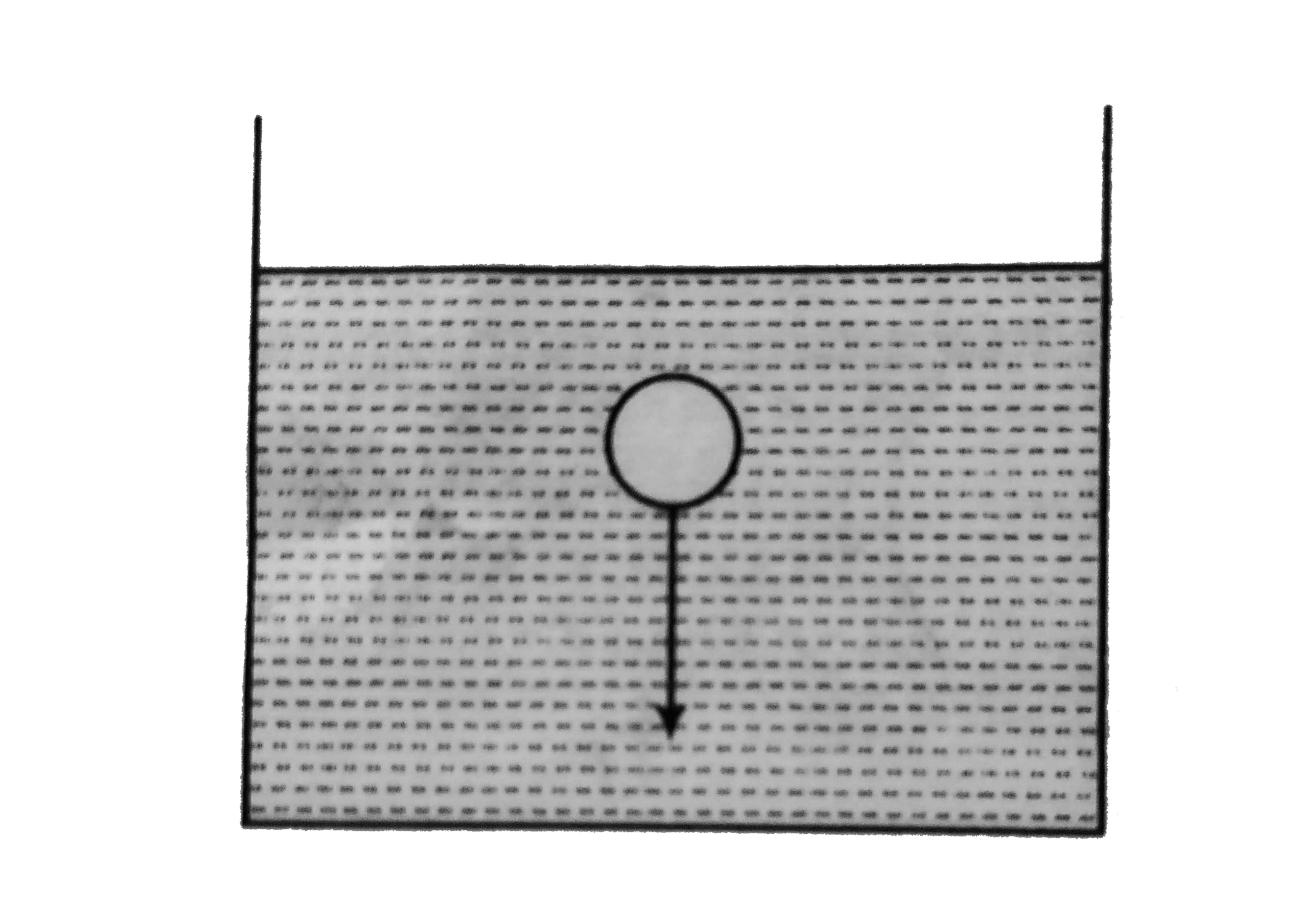
A ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.
The correct Answer is:A, B, D
Decrease in potential energy of the ball.
=m1gh(m1=mass of ball)
=(Vρ1)gd
or, ΔU1=−Vρ1gd
When Vvolume of solid comes down, then it is replaced by V volume of liquid.
∴ Increase in potential energy of liquid:
=m2gh(m2=mass of liquid of volume V)
=(Vρ2)gd
or, ∴ΔU2=−Vρ2gd
Total change in potential energy.
ΔU=ΔU1+ΔU2=V(ρ2−(ρ1)gd.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.16videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Introductory Exercise1videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples21videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
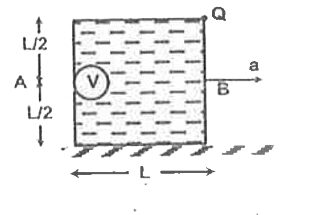
A small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
 View Solution
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View Solution
Knowledge Check
- Question 1 - Select One
A body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:
AVdgBVρgCV(ρ−d)gDV(d−ρ)g - Question 2 - Select One
A ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
Awith an increasing accelerationBwith a decreasing accelerationCwith a constant accelerationDwith zero acceleration - Question 3 - Select One
A solid ball of density ρ1 and radius r falls vertically through a liquid of density ρ2. Assume that the viscous force acting on the ball is F=krv, where k is a constant and v its velocity. What is the terminal velocity of the ball ?
A(4πgr2ρ1−ρ23k)B(2πrρ1−ρ22gk)C(2πg(ρ1+ρ2)3gr2k)DNone of these
A ball of density ρ0 falls from rest from a point P onto the surface of a liquid of density ρ in the time T. It enters the liquid, stops, moves up, and returns to P in a total time 3 T. neglect viscosity, surface tension and splashing find the ratio of ρρ0
View SolutionA block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionA body of volume V and desnity ρ is initially submerged in a non-viscous liquid of density σ(>ρ). If it is rises by itself through a height h in the liquid. Its kinetic energy will
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View Solution

