Figure shown a container having liquid of variable density. The density of liquid veriesas ρ=ρ0(4−3hh0). Here, h0 and ρ0 are constants and h is measured from bottom of the container. A solid block of small dimensions whose density is 52ρ0 and mass m is released from bottom of the tank. Prove that the block will execute simple harmonic motion. Find the frequency of oscillation.
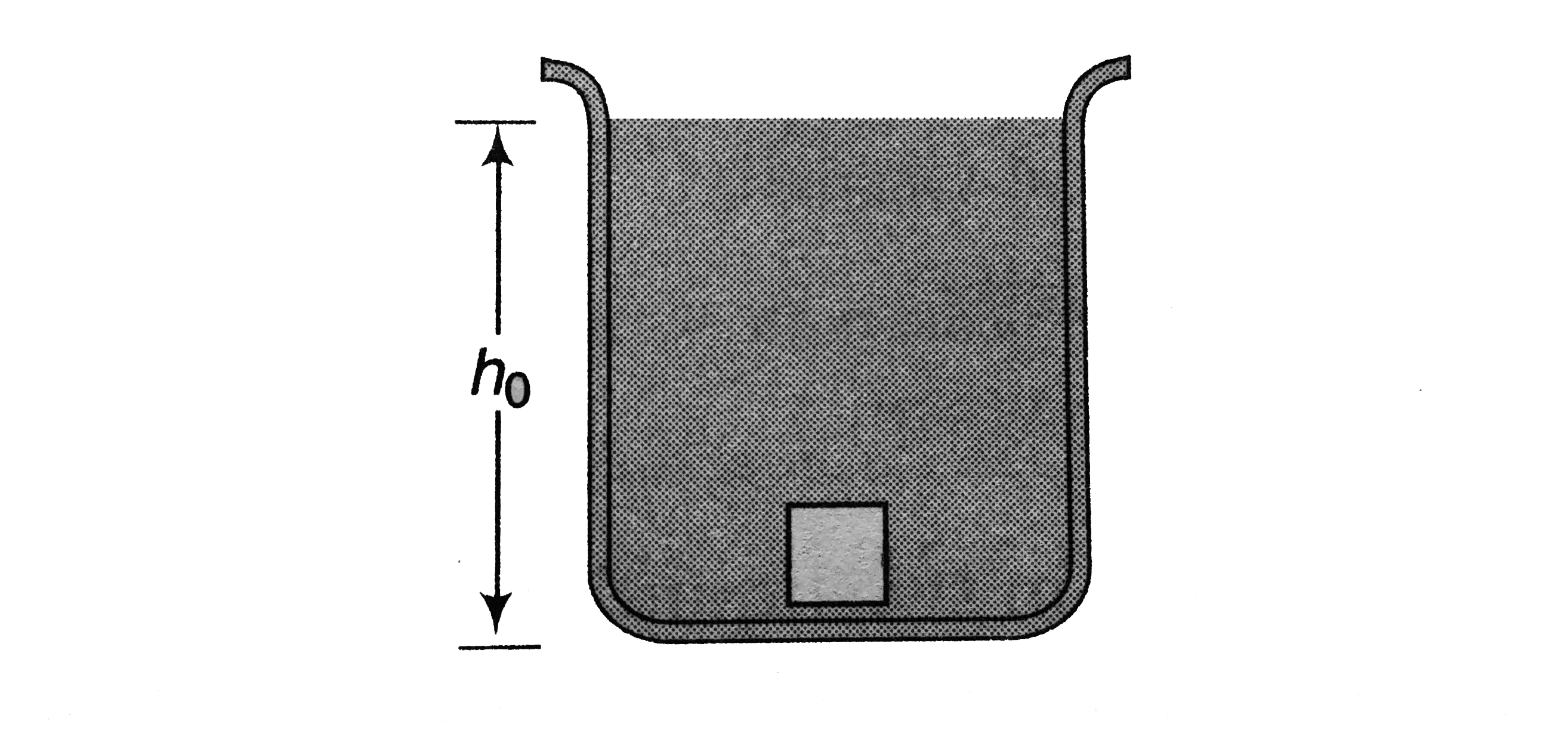 .
.
Net force on the block at a height h from the bottom is
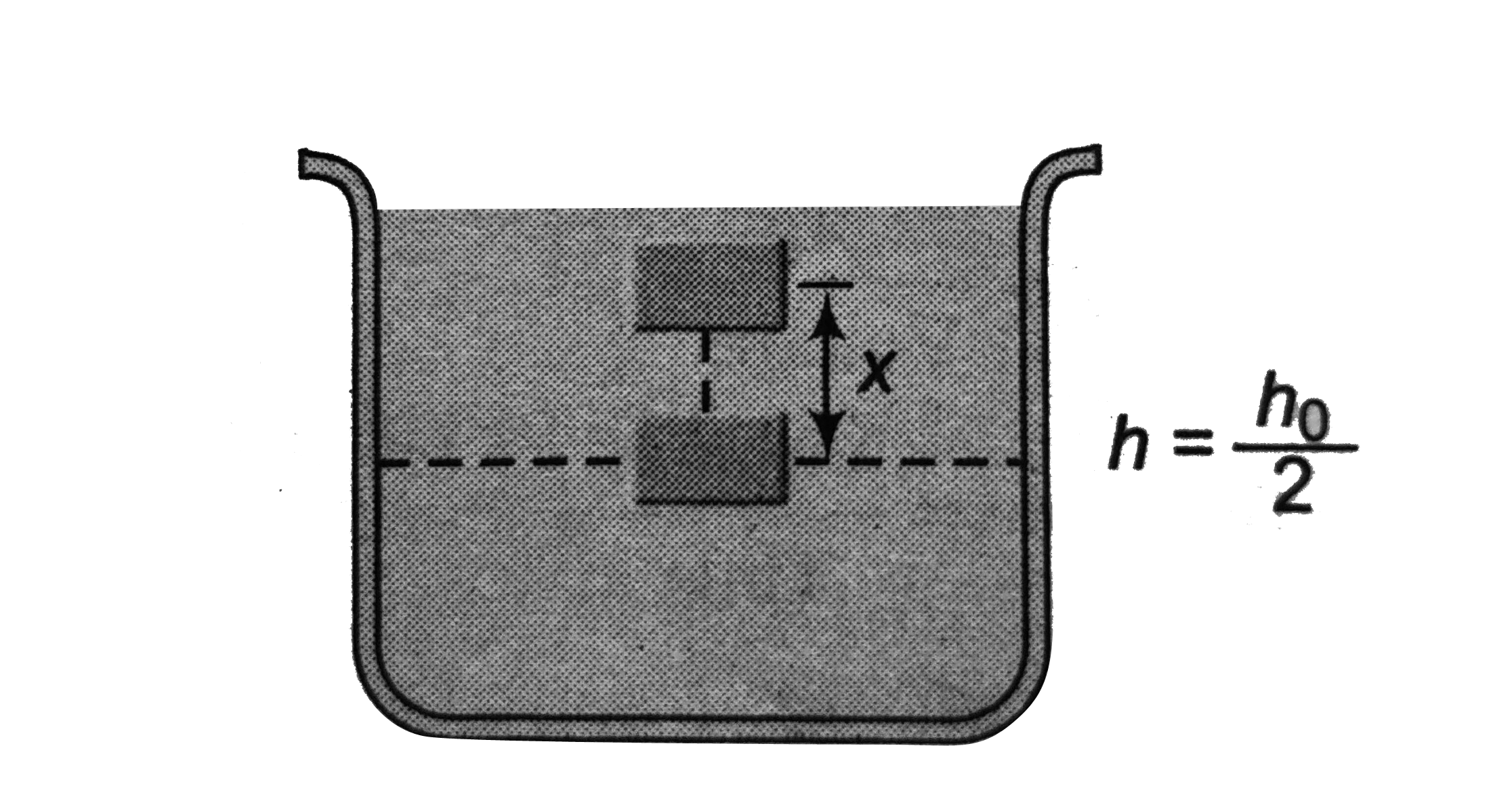
Fnet=upthrust-weight (upwards)
=⎛⎝m52ρ0⎞⎠ρ0(4−3hh0)g−mg
Fnet=0ath=h02
so, h=h02 is the equilibrium positive of the block.
For h>h02 weightgtuupthrust
i.e. net force is downwards and for h<h02
weight lt upthrust
i.e. net force is upwards
For upward displacement x from mean position, net downward force is
F=−⎡⎣⎛⎝m52ρ0⎞⎠ρ0{4−3(h−x)h0}g−mg⎤⎦(h=h02)
∴F=−6mg5h0x ....(i)
(because at h=h02 upthrust and weight are equal)
since, F∝−x
Oscillations are simple harmonic in nature Rewriting Eq. (i)
ma=−6mgx5h0
or, a=−6g5h0x
∴f=12π√∣∣ax∣∣
f=12π√6g5h0.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.11videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.21videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based7videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the mass M of the rod.View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥RView Solution
Knowledge Check
- Question 1 - Select One
A solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
A2π√ρ0ρagB2π√ρρ0agC2π ⎷a(1−ρρ0)gD2π ⎷a(1+ρρ0)g - Question 2 - Select One
The density ρ of a liquid varies with depth h from the free surface as ρ=kh. A small body of density ρ1 is released from the surface of liquid. The body will
Acome to a momentary rest at a depth 2ρ1/k from the free surfaceBexecute S.H.M. about a point at a depth ρ1/k from the surfaceCexecute S.H.M. of amplitude ρ1/kDall of these - Question 3 - Select One or More
Density of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
Athe ball will execute SHM of amplitude ρ0αBthe mean position of the ball will be at a depth ρ02αCthe ball will sink to a maximum depth of ρ0αDThe ball sink to a maximum depth of ρ0α
A solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe linear mass density i.e. mass per unit length of a rod of length L is given by ρ=ρ0(1+xL), where ρ0 is constant , x distance from the left end. Find the total mass of rod and locate c.m. from the left end.
 View Solution
View SolutionIn the arrangement as shown, mB=3m, density of liquid is ρ and density of block B is 2ρ. The system is released from rest so that block B moves up when in liquid and moves down when out of liquid with the same acceleration. Find the mass of block A.
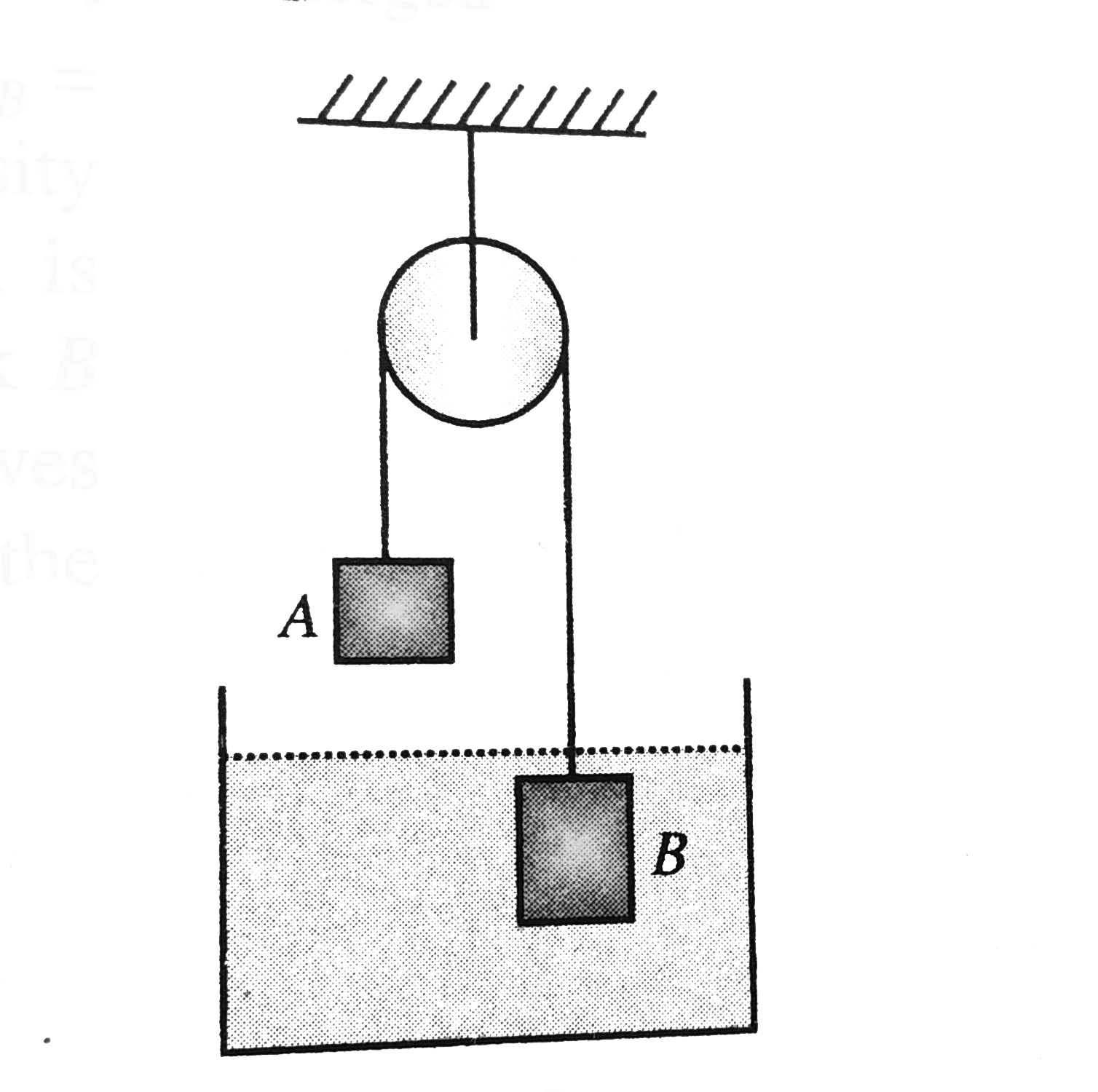 View Solution
View SolutionA wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
View Solution

