The shape of an ancient water clock jug is such that water level descends at a constant rate at all time. If the water level falls by 4cm every hour, determine the shape of the jar, i.e. specify x as a function of y. The radius of drain hole in 2mm and can be assumed to be very small compared to x.
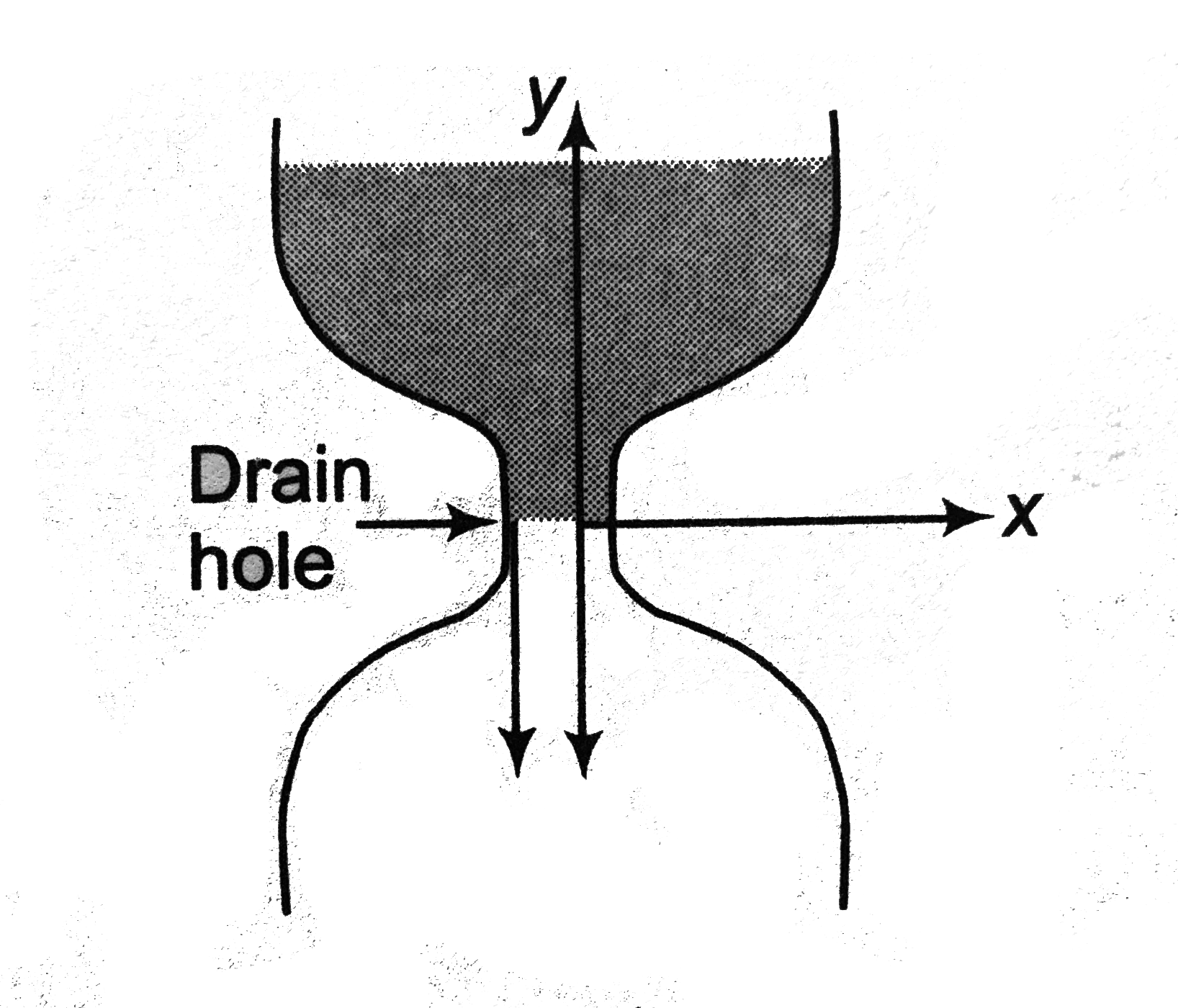
The correct Answer is:D
a√2gy=πx2(−dydt)
Here, −dydt=4×10−23600=1.11×10−5m/s
a=πr2=π(2×10−3)2
=1.26×10−5m2
substituting these values in Eq, (i) we have
(1.26×10−5)√2×9.8×y=π(1.11×10−5)x2
or, y=0.4x4
This is the desired x-y relation.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct
36 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A water clock consist of a vessel which has a small orifice O. The upper contaienr is filled with water which trickless down into the lower contaienr. The shape of the (upper or lower) contaienr is such that height of water in the upeer container changes at a uniform rate. What should be the shape of the container? Assume that atmospheric air can enter inside the lower container through a hole in it taht the upper container is open at the top. Vessel is axially symmetric.

View SolutionA vessel in the shape of a cuboid contains some water. If three indentical spheres are immersed in the water, the level of water is increased by 2cm. If the area of the base of the cuboid is 160 cm2 and its height 12cm, determine the radius of any of the spheres.
View Solution
Knowledge Check
An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)

Ley ycm(t) denote the height of the centre of mass of all the water that has collected in the beaker by time t. what is the rate at which this height increaes (i.e. dy(cm)/dt?AuBu2CVolume strengthDv2An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
Choose the incorrect option.ARate at which the mass of the water in the beaker increaes with time is Pau.BAt a given time the water in the beaker has total vertical momentum.CThe mass of the water in the beaker at a given time is pADnone of the above optionsAn initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
If the beaker is placed on a weighing scale, while the beaker is wstill in the rain, the impact of the raindrops on the beaker will cause the reading on the scale increased by the impact of the raindrops ? (Neglect the effect of raindrops that hit the scale directily).ApAv2gBpAu2gCpAuVgDpAuv2g
A vessel in the shape of a cuboid contains some water. If three indentical spheres are immersed in the water, the level of water is increased by 2cm. If the area of the base of the cuboid is 160 cm2 and its height 12cm, determine the radius of any of the spheres.
View SolutionA water tank has the shape of a cube with each side of length 3 metre. Water is poured into it at a constant rate of 27 cubic metre per hour. Then,the rate at which the level of the water is rising at the instant, when the depth of water in the tank is x,(0<x<2), is (in metre per hour) (i)x (ii) 3x (iii) 9x (iv) 3
View SolutionA 3.6m long vertical pipe resonates with a source of frequency 212.5Hz when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height H(≈3.6m). A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of H. If the radii of the pipe and the hole are 2×10−2m and 1×10−3m respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air 340m/s and g=10m/s2.
View SolutionA 3.6m long vertical pipe resonates with a source of frequency 212.5Hz when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height H(≈3.6m). A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of H. If the radii of the pipe and the hole are 2×10−2m and 1×10−3m respectively, calculate the time interval between the occurance of first two resonances. Speed of sound in air 340m/s and g=10m/s2.
View SolutionA water clock used in ancient Greek is designed as a closed vessel with a small orifice O. The time is determined accrding to the level of the water in the vessel. What should be the shape of the vessel be for the time scale to be uniform. Find mathemtical equation governing curve AOB.
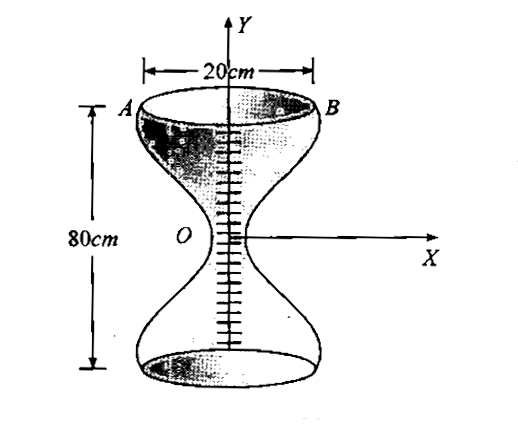
View Solution
