Question

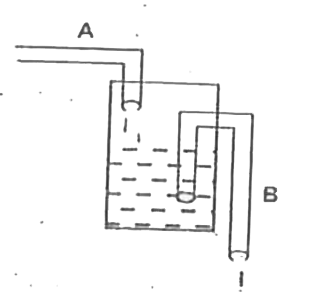
A $3.6m$ long vertical pipe resonates with a source of frequency $212.5Hz$ when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height $H(\approx 3.6m)$. A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of $H$. If the radii of the pipe and the hole are $2\times {10}^{-2}m$ and $1\times {10}^{-3}m$ respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air $340m/s$ and $g=10m/s^2$.

Answer

`h=3.2,2.4,1.6,0.8,v=5xx10^(-3)sqrt(5H),Deltat=80(4-2 sqrt(3))`

Explanation

To solve the problem step by step, we will break it down into parts as outlined in the question.

Part 1: Finding the Height of Water Level for Resonance

1. Identify the Length of the Pipe and Frequency:
- Length of the pipe, \( L = 3.6 \, \text{m} \)
- Frequency of resonance, \( f = 212.5 \, \text{Hz} \)
- Speed of sound in air, \( v = 340 \, \text{m/s} \)

2. Determine the Fundamental Frequency of a Closed Pipe:
- For a closed organ pipe, the fundamental frequency is given by:
\( f = \frac{v}{4L} \)
- Rearranging for \( L \):
\( L = \frac{v}{4f} \)

3. Calculate the Fundamental Length:
- Substitute the values:
\( L = \frac{340}{4 \times 212.5} = \frac{340}{850} = 0.4 \, \text{m} \)

4. Identify Other Resonant Lengths:
- The lengths of the air column that resonate are given by:
\( L_n = n \cdot L \quad \text{where } n = 1, 3, 5, \ldots \)
- Calculate the first few lengths:
- For \( n=1 \): \( L_1 = 0.4 \, \text{m} \)
- For \( n=3 \): \( L_3 = 1.2 \, \text{m} \)
- For \( n=5 \): \( L_5 = 2.0 \, \text{m} \)
- For \( n=7 \): \( L_7 = 2.8 \, \text{m} \)
- For \( n=9 \): \( L_9 = 3.6 \, \text{m} \)

5. Calculate the Corresponding Water Heights:
- The height of water level \( H \) when resonance occurs is given by:
\( H_n = 3.6 - L_n \)
- Calculate:
- For \( n=1 \): \( H_1 = 3.6 - 0.4 = 3.2 \, \text{m} \)
- For \( n=3 \): \( H_3 = 3.6 - 1.2 = 2.4 \, \text{m} \)
- For \( n=5 \): \( H_5 = 3.6 - 2.0 = 1.6 \, \text{m} \)
- For \( n=7 \): \( H_7 = 3.6 - 2.8 = 0.8 \, \text{m} \)
- For \( n=9 \): \( H_9 = 3.6 - 3.6 = 0 \, \text{m} \)

Part 2: Rate of Fall of Water Level

1. Define the Variables:
- Let \( H \) be the height of water in the pipe.
- The area of the pipe \( A = \pi R^2 \) where \( R = 2 \times 10^{-2} \, \text{m} \).
- The area of the hole \( a = \pi r^2 \) where \( r = 1 \times 10^{-3} \, \text{m} \).

2. Velocity of Efflux:
- The velocity of water flowing out of the hole is given by Torricelli’s law:
\( v = \sqrt{2gH} \)

3. Volume Flow Rate:
- The volume flow rate out of the hole:
\( Q_{\text{out}} = a \cdot v = \pi r^2 \cdot \sqrt{2gH} \)
- The decrease in volume flow rate in the pipe:
\( Q_{\text{in}} = A \frac{dH}{dt} = \pi R^2 \frac{dH}{dt} \)

4. Equate the Flow Rates:
- Set the volume flow rates equal:
\( \pi R^2 \frac{dH}{dt} = -\pi r^2 \sqrt{2gH} \)

5. Simplify the Equation:
- Cancel \( \pi \) and rearrange:
\( \frac{dH}{dt} = -\frac{r^2}{R^2} \sqrt{2gH} \)

Part 3: Time Interval Between First Two Resonances

1. Integrate the Equation:
- We need to find the time interval \( t \) between \( H = 3.2 \, \text{m} \) and \( H = 2.4 \, \text{m} \):
\( \int_{3.2}^{2.4} \frac{dH}{\sqrt{H}} = -\frac{r^2}{R^2} \sqrt{2g} \int_0^t dt \)

2. Calculate the Integral:
- The left-hand side integrates to:
\( 2(\sqrt{2.4} - \sqrt{3.2}) = -\frac{r^2}{R^2} \sqrt{2g} t \)

3. Substitute Values:
- Substitute \( r = 1 \times 10^{-3} \, \text{m} \), \( R = 2 \times 10^{-2} \, \text{m} \), and \( g = 10 \, \text{m/s}^2 \):
\( t = \frac{2(\sqrt{2.4} - \sqrt{3.2})}{\frac{(1 \times 10^{-3})^2}{(2 \times 10^{-2})^2} \sqrt{20}} \)

4. Calculate the Final Result:
- After performing the calculations, we find:
\( t \approx 43 \, \text{s} \)

Final Answers:
- Height of water level for first resonance: \( 3.2 \, \text{m} \)
- Height of water level for second resonance: \( 2.4 \, \text{m} \)
- Time interval between first two resonances: \( 43 \, \text{s} \)