Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
The correct Answer is:A, B, C, D
Let T1 be the temperature of C1 and T2 the temperature of C2 at some intant of time. Further let T be the temperature difference at that instant.

Then,
C1(−dT1dt)=H=Tl/KA=KAl(T)
and C2(+dT2dt)=H=Tl/KA=KAl(T)
∴−dTdt=−dT1dt+dT2dt
∴−dT1dt=KAlC1(T)
and +dT2dt=KAlC2
Further, −dTdt=−dT1dt+dT2dt
=KA(C1+C2)lC1C1T
or ∫TΔT0dTT=−KA(C1+C2)lC1C2∫t0dt
Solving, we get T=ΔT0e−αt
where, α=KA(C1+C2)lC1C2.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct
5 Videos
- BASIC MATHEMATICSBOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the fisrt body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionTwo chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time.
View Solution
Knowledge Check
A rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
AAα(T21−T22)lBAα(T21+T22)lCAα(T21+T22)3lDAα(T21−T22)2lTwo adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
AmsLAδtBemsLAδtCmsL2eAδtDmsL2AδtTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
When two bodies ofmasses m1 and m2 with specific heats s1 and s2 at absolute temperatures T10 and T20(T10>T20) are connected by a rod of length l and cross sectional area A with thermal conductivity k. Find the temperature difference of the bodies after time t. Neglect any heat loss due to radiation at any surface..

View SolutionTwo bodies each of mass m, having specific heats s, are connected by ametal rod of negligible heat capacity of length l, area of cross section A and thermal conductivity k. Initially both bodies are at different temperatures, find the time taken for the temperature difference between the two bodies to become half of the. initial value.
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
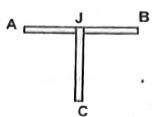
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View SolutionThe temperature of an spherical isolated black body falls from T1 and T2 in time t them time t is
View SolutionThe temperature of an isolated black body falls from T1 to T2 in time t. Let c be a constant
View Solution