A uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
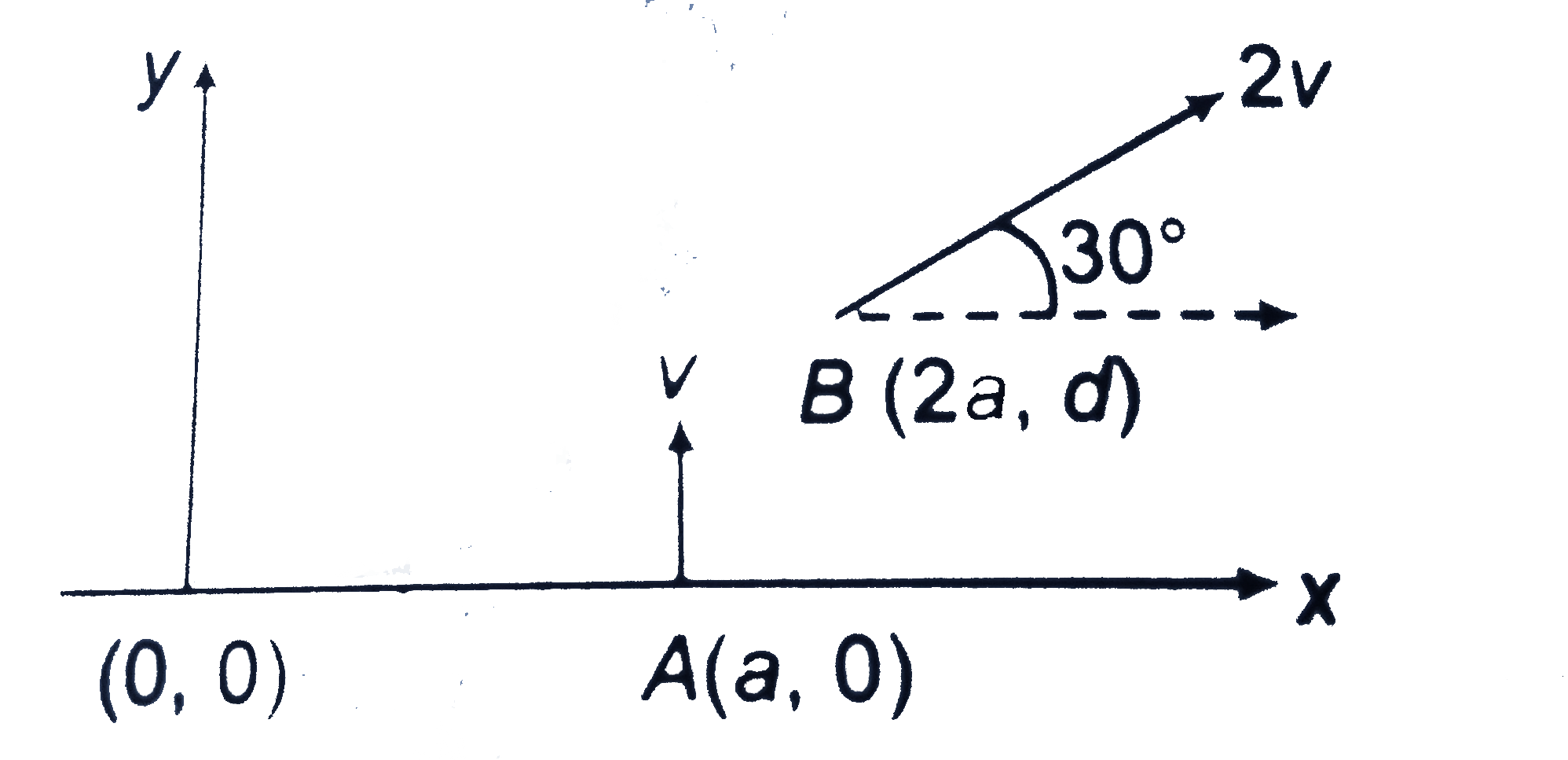
electric field E=3mv22eaˆi
rate of doing work doen by electric field ast B is 3mv22ea
Bota a and b are correct
both a and b are wrong
The correct Answer is:A
(vA)y=v⇒(vB)y=2vsin30∘v
Since y-component of velocity remains unchanged. Hence electric field is along (−ˆi) direction. Work done by electrostatic force in moving from A and B =change in its kinetic energy
∴(eE)(2a−a)12m(4v2−v2)
E=mv22ea
orE=−3mv22eaˆi
Rate of doing work done =power
=Fvcosθ
(3mv22ea)2(e)(2v)cos30∘
=3√32mv2a
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Objective
82 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
The electric field and the electric potential at a point are E and V respectively.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
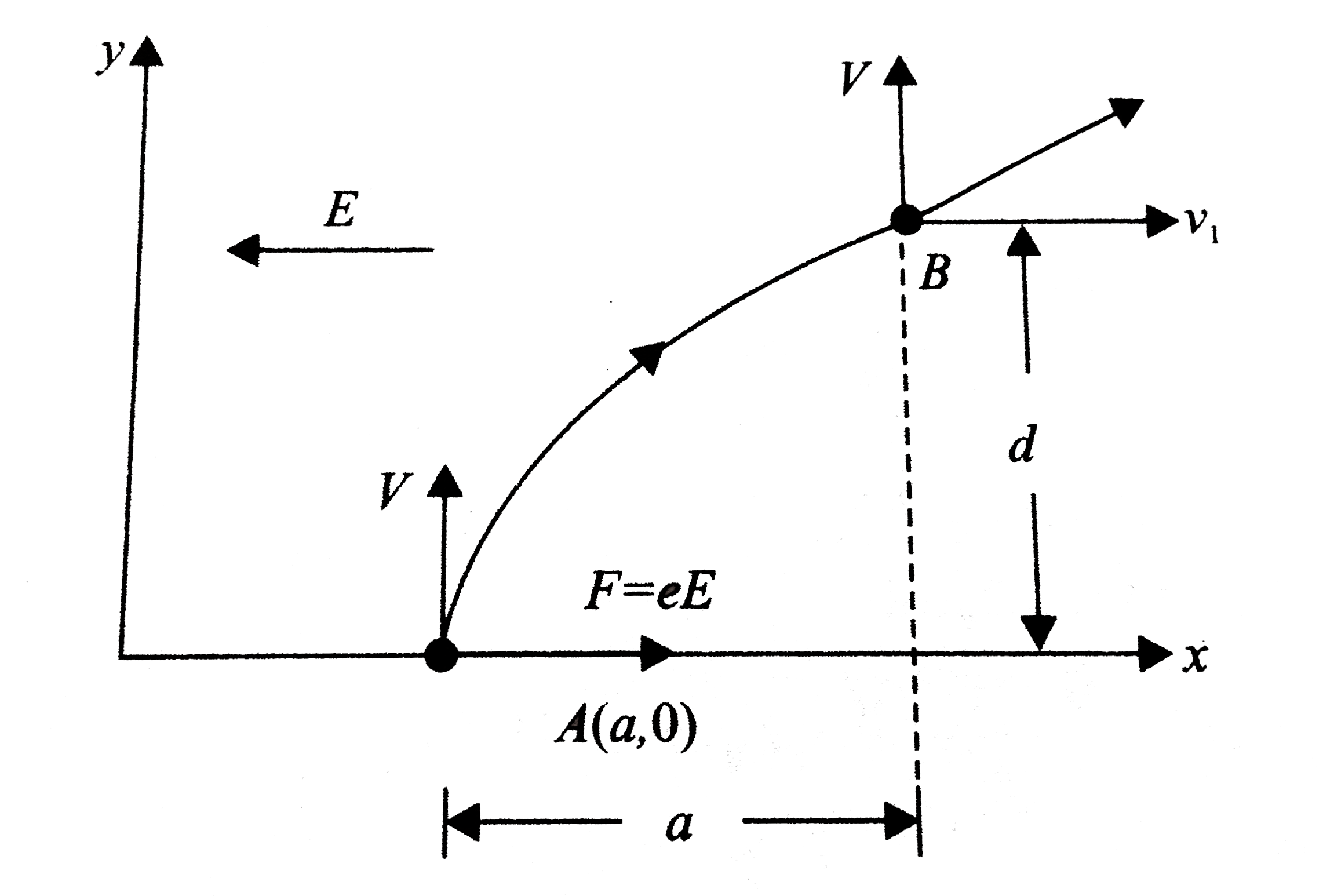
Find the rate of work done by the field at B.
View Solution
Knowledge Check
A uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity Vˆj. It moves through the electric field & exits at point B. Then :
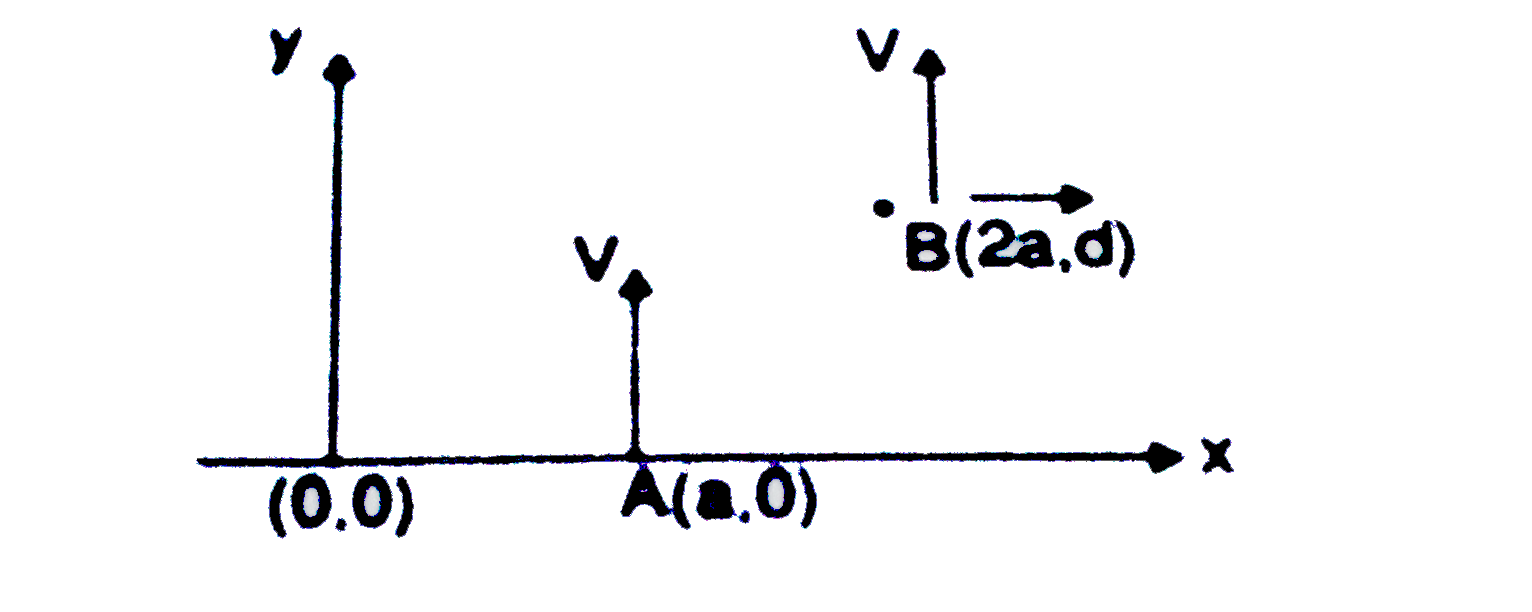 A→E=−2amv2ed2ˆi.BRate of work done by the electric field at B is 4ma2v3d3CRate of work by the electric field at A is zero.DVelocity at B is 2avdˆi+vˆj.
A→E=−2amv2ed2ˆi.BRate of work done by the electric field at B is 4ma2v3d3CRate of work by the electric field at A is zero.DVelocity at B is 2avdˆi+vˆj.An uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
 .
.
Find electric field.A2maV2ed2BmaV2ed2CmaV22ed2D2maV3ed3An uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
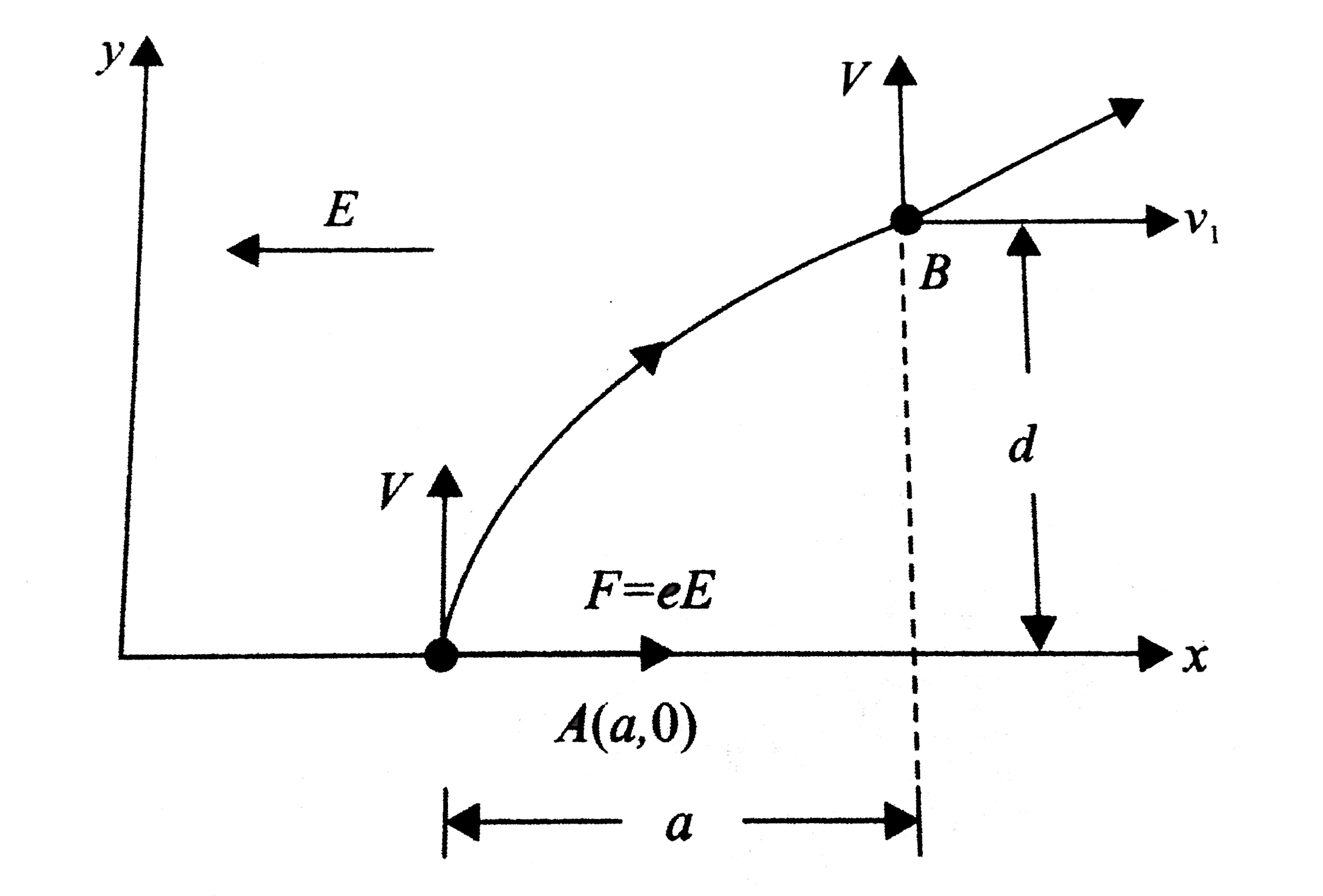 .
.
Find velocity at B.AV√1−(2ad)2BV√1+(2ad)2CV√1+(ad)2DV√2+(2ad)2
An electron enters in an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionA uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will
View SolutionA uniform electric field and a uniform magnetic field exist in a region in the same direction. An electron is projected with a velocity pointed I the same direction. Then the electron will:
View SolutionA charged particle moving with velocity vis subjected to electric field E and magnetic field B. The particle will go undeflected if
View SolutionElectric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
View Solution