A capacitor of capacitance as C is given a charge Q. At $t = 0$ ,it is connected to an ideal battery of emf $(ε)$ through a resistance R. Find the charge on the capacitor at time t.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$q_{i} = q_{0}$
$q_{f} = E C$
Now, charge on capacitor change from $q_{i}$ to $q_{f}$ exponentially.

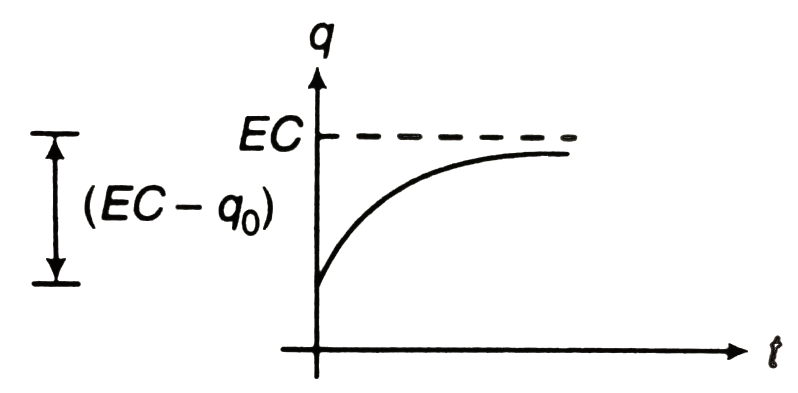
$∴ q = q_{0} + (E C - q_{0}) (1 - e^{- \frac{1}{τ_{C}}})$
$= E C (1 - e^{- \frac{t}{τ_{C}}}) + q_{0} e^{- \frac{t}{τ_{C}}})$
Here $τ_{C} = C R$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is
A $\frac{Q^{2}}{2 C}$
B $\frac{Q^{2}}{4 C}$
C $\frac{Q^{2}}{8 C}$
Ddependent on the value of the resistance
Question 2 - Select One
A capacitor of capacitance C is given charge Q and then connected in parallel to a coil of inductance L. There is no resitance in the circuit. When the charge on the capacitor becomes zero, the current in the coil will be
A $Q \sqrt{\frac{L}{C}}$
B $\frac{Q}{\sqrt{L C}}$
C $Q \sqrt{\frac{C}{L}}$
Dzero
Question 3 - Select One

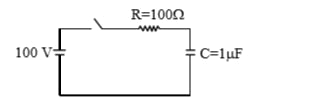
A capacitor of capacitance C=1 $μ F$ is suddenly connected to a battery of 100 volt through a resistance $R = 100 Ω$ . The time taken for the capacitor to be charged to get 50 V is :
[Take ln 2 = 0.69]
A $1.44 \times 10^{- 4} s$
B $3.33 \times 10^{- 4} s$
C $0.69 \times 10^{- 4} s$
D $0.30 \times 10^{- 4} s$

DC PANDEY-CAPACITORS-Exercise

Home
Ask Doubt
Profile