A capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
Let at any time,
q=εc(1−e−trc)
E=e≠rgys→red
=q22c=(ε2C22C)(1−e−trc)2
=(1+e−trc)2
r=rateofe≠rgys→red
=(dεdT)=(−ε2C2)drdt
=(1−e−trc)
drdte−trc=(dε2r)(−1rC2)(e−trc(1−e−trc)
ε22r=[(e−trc)(1−e−trc)+(−).(e−trc)(−1rc)(e−trc)]
ε2r=(ε2r+ε2r+12r(e−2tcr))
=(2rC)e−2tcrεrC)
Forrmax'drdt=0
⇒2.(e−trc=0
⇒e−trc=12
⇒=−trc=−In2⇒t=rcIn2
Pu∈gt=In2∈equation(i)
we≥t,drdt=ε24r.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
Similar Questions
A capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionAn inductance L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View Solution
Knowledge Check
An uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :A10 J/sB20 J/sC40 J/sD5 J/sAn inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4RεAn inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4Rε
A capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance C is connected to a battery of emf V through a resistance R with a switch connected in series .Switch is turned on at t=0 . Find the displacement current flowing between the plates of capacitor as a function of time .
View SolutionA capacitor of capacitance 200μF is connected to a battery through a resistance of 5kΩ at time t = 0. Charge stored in the capacitor in first second in larger than the charge stored in the next
View SolutionA capacitor of capacitance 13μF is connected to a battery of 300volt and charged. Then the energy stored in capacitor is
View Solution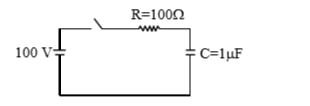
A capacitor of capacitance C=1 μF is suddenly connected to a battery of 100 volt through a resistance R=100Ω . The time taken for the capacitor to be charged to get 50 V is :
[Take ln 2 = 0.69]
View Solution
