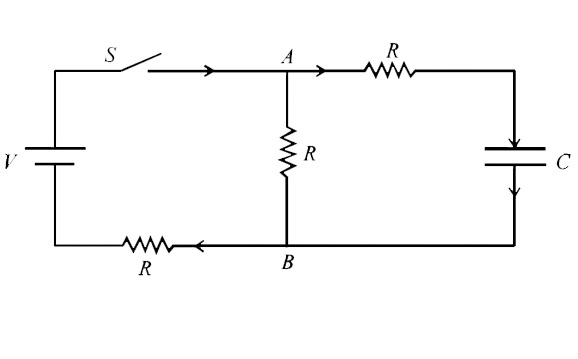
In the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its limiting value as t→∞:
 .
.
The correct Answer is:B, C
a. In steady state,
VC=V2
∴ Steady state charges,
q0=CVC=CV2
For equivalent value of τC: we short circuit the battery and find the value of R≠t across capacitors and then
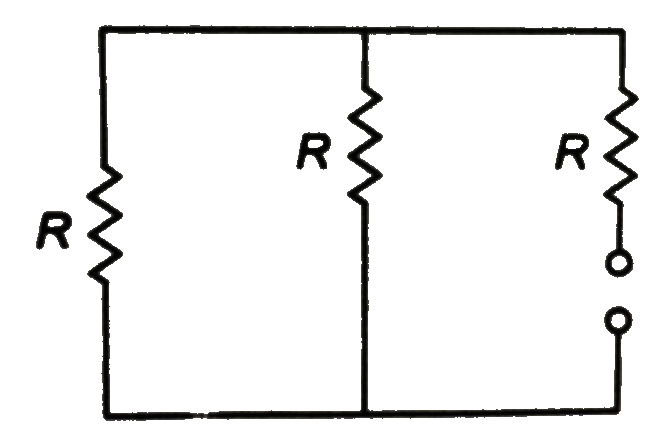
R≠t=3R2
∴τC=CR≠t=3RC2
Now,q=q0(1−e−tτC)
b. At t=0 capacitor offers zero resistance
R≠t=3R2
∴i=V3R2=2V3R
iC=iAB=12=V3R
Att=∞ capacitor offers infinite resistance. So, iC=0
∴ibaery=iAB=V2R
Now current through AB increases exponentially from V3R→V2R with same time constant.
(i−t) graph is as shown below.
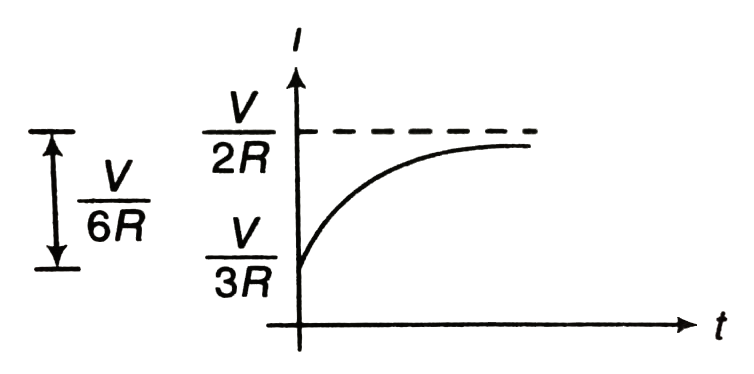
(i-t) equation corresponding to this graph is
i=V3R+V6R(1−e−tτC)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
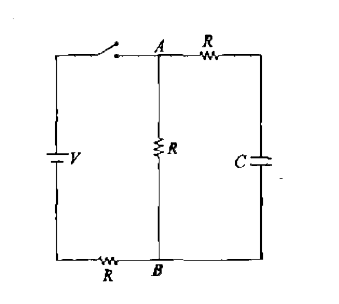
In the circuit shown in figure-3.244, the battery is an ideal one with emf V. The capacitor is initially uncharged. The switch S is closed at time t=0.
(a) Find the charge Q on the capacitor at time l
(b) Find the current in branch AB at time just after closing the switch.
 View Solution
View SolutionIn the circnit shown, capacitor is initially uncharged till the switch is turned on at time t=0. Then
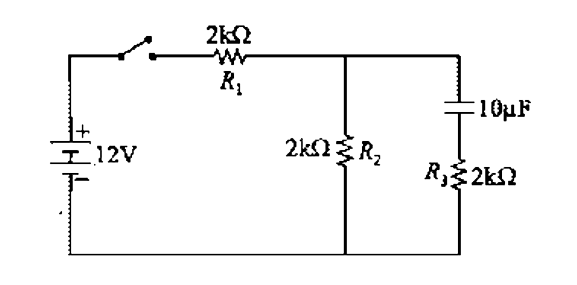 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
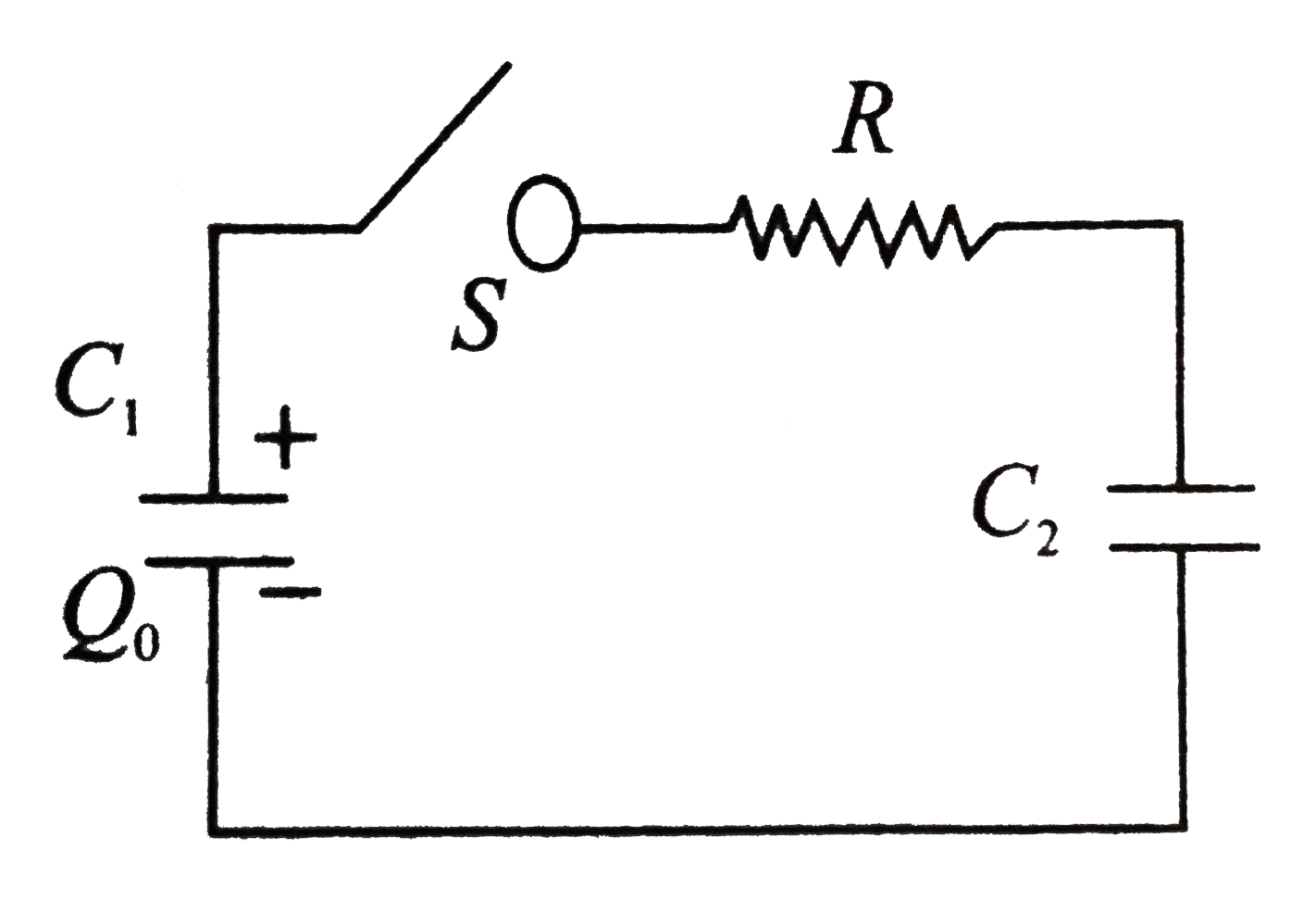 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R) - Question 2 - Select One
In the circuit shown, the capacitor is initially uncharged. The switch S is closed at t = 0. Time after which voltage across capacitor and resistor are equal is:
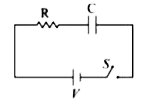 ARCln12BRCln2CRCln32DRC
ARCln12BRCln2CRCln32DRC - Question 3 - Select One
The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
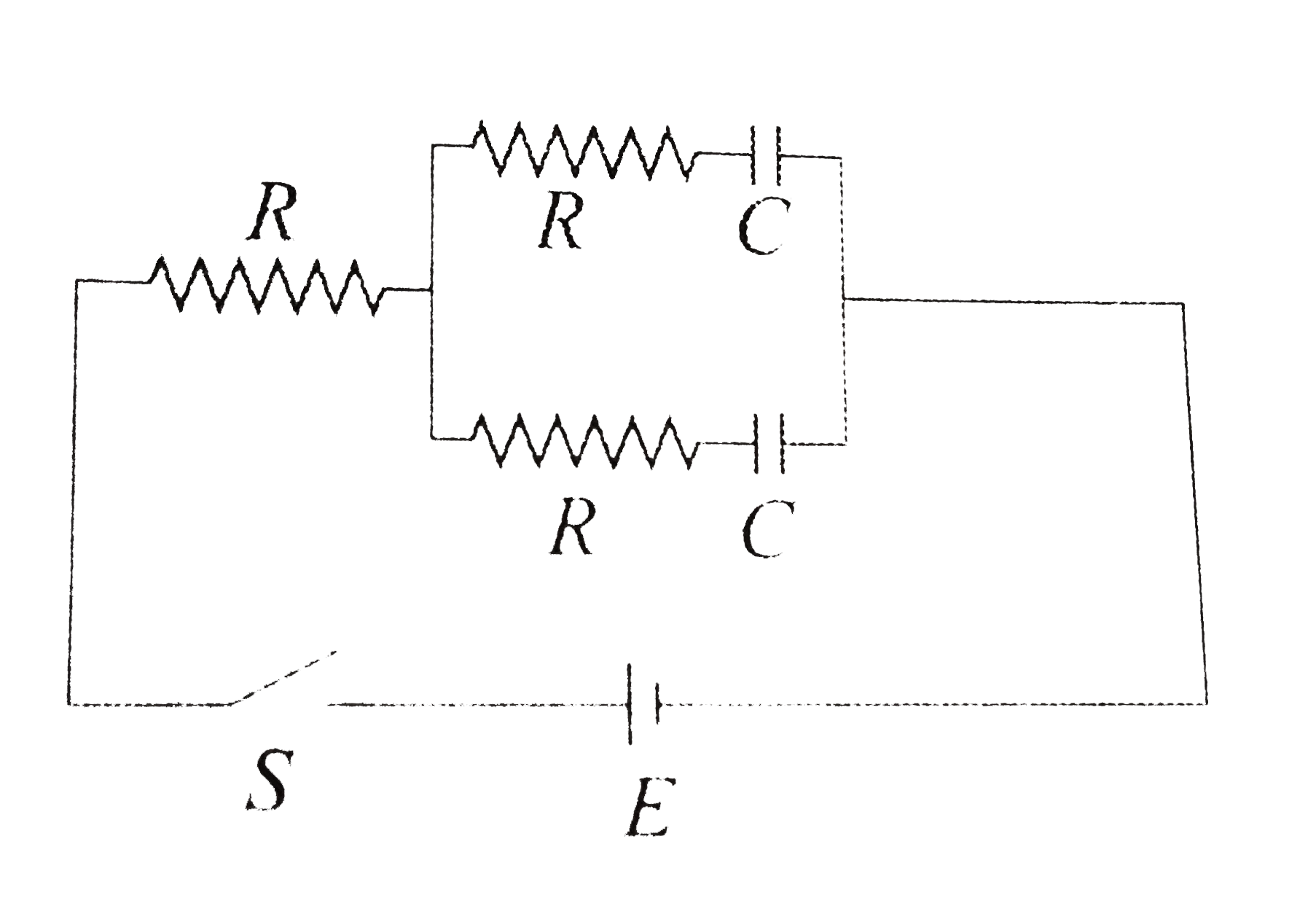 Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)
Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)
In the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
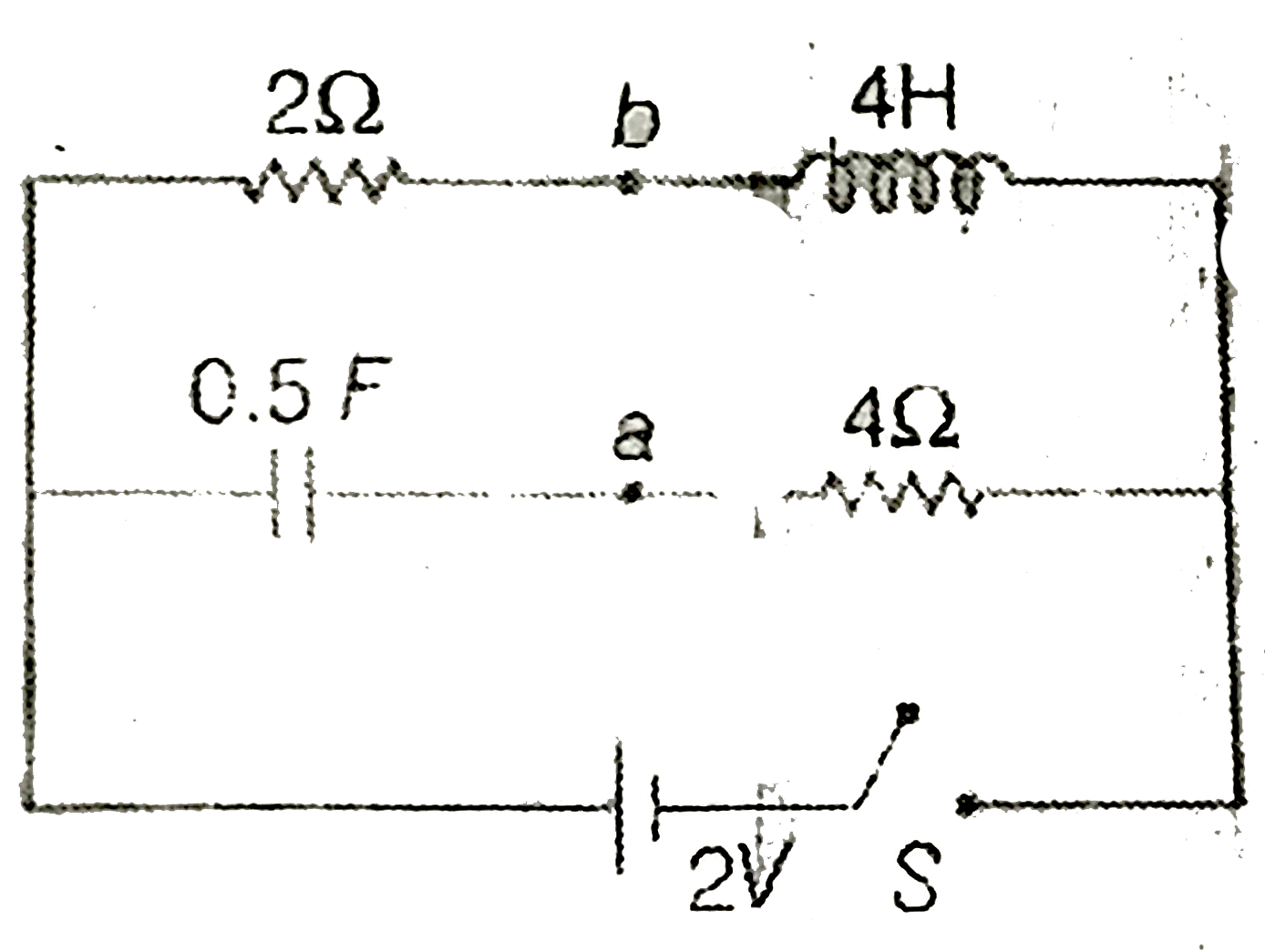 View Solution
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t
 View Solution
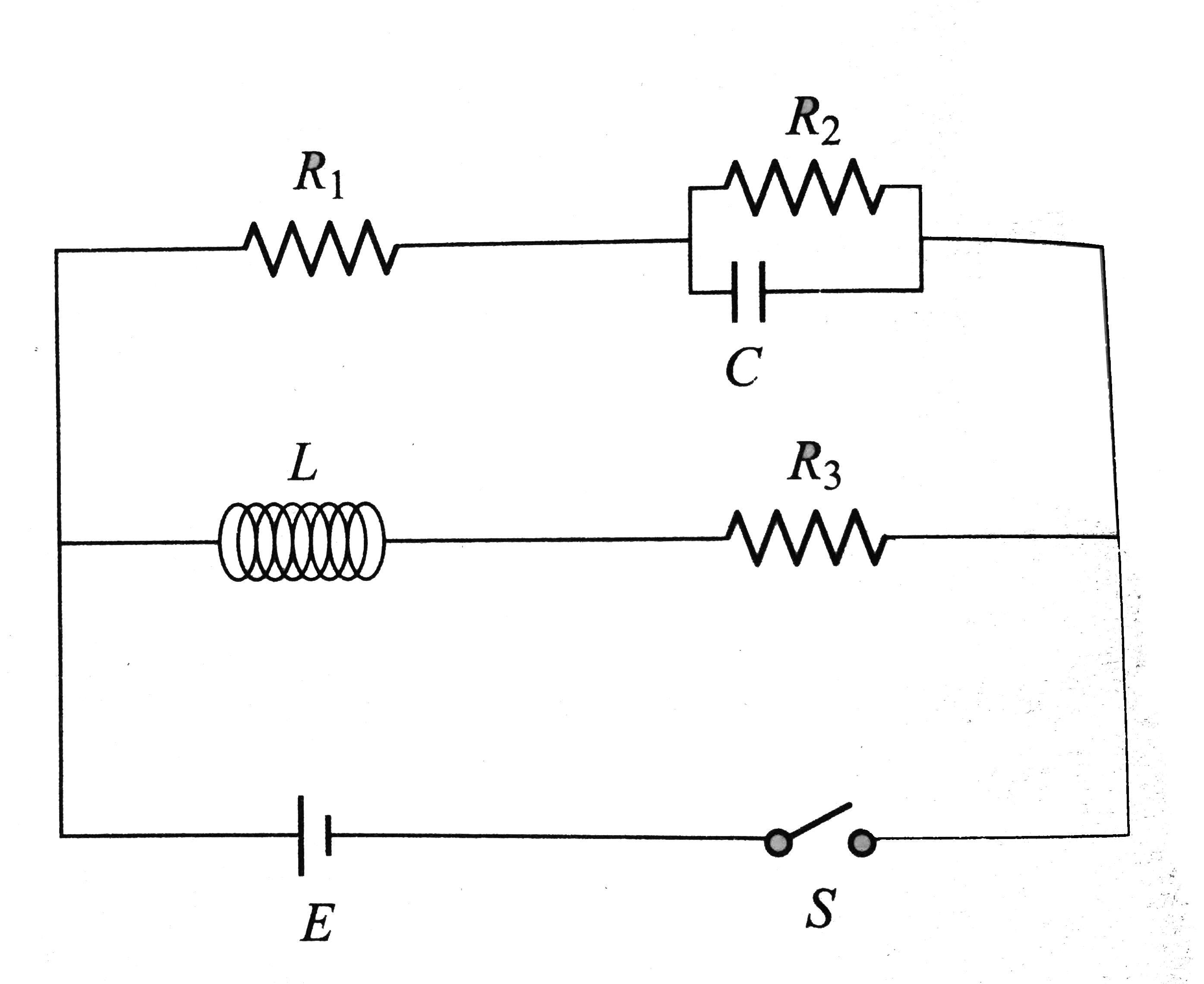
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
 View Solution
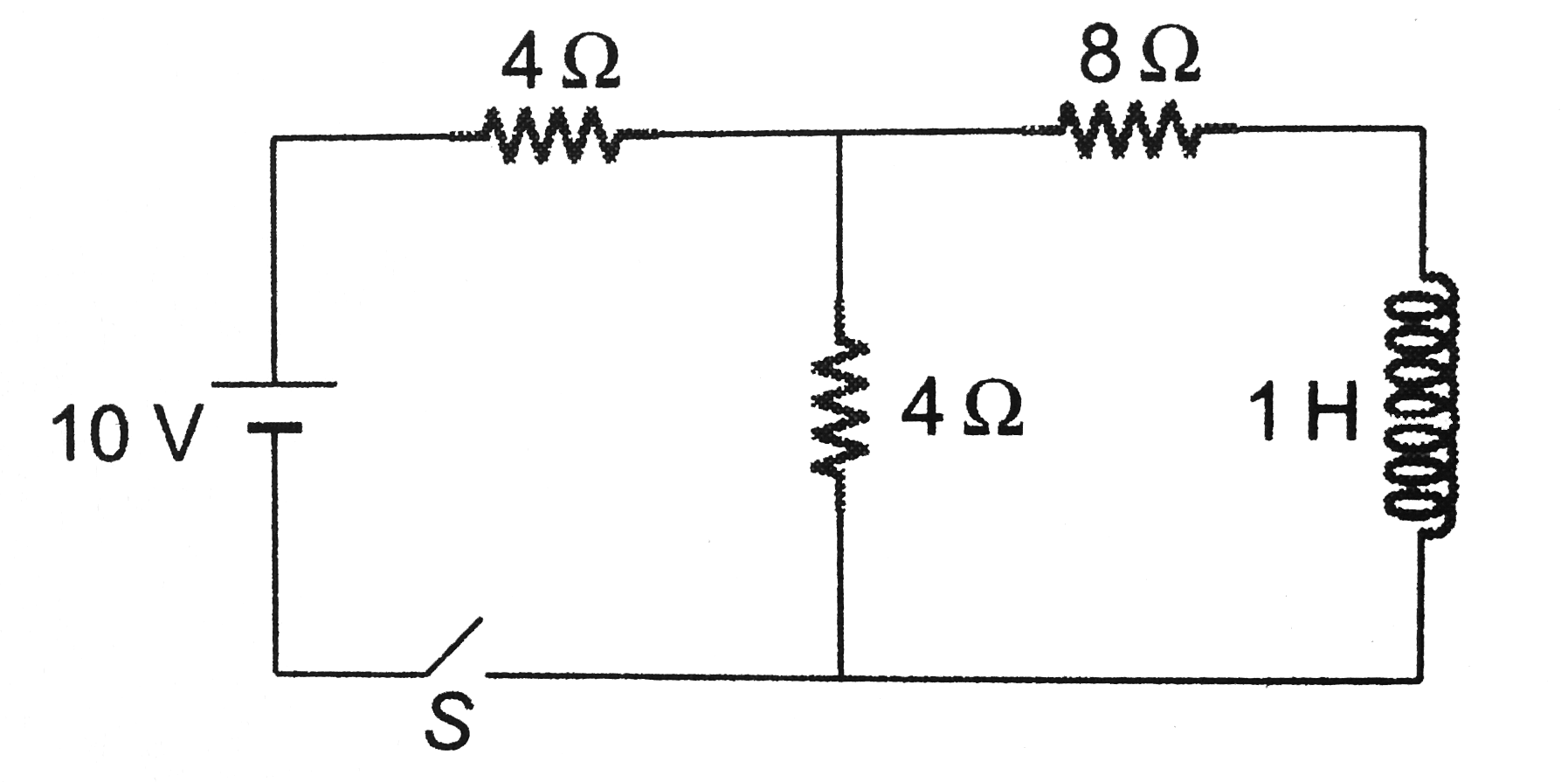
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png) View Solution
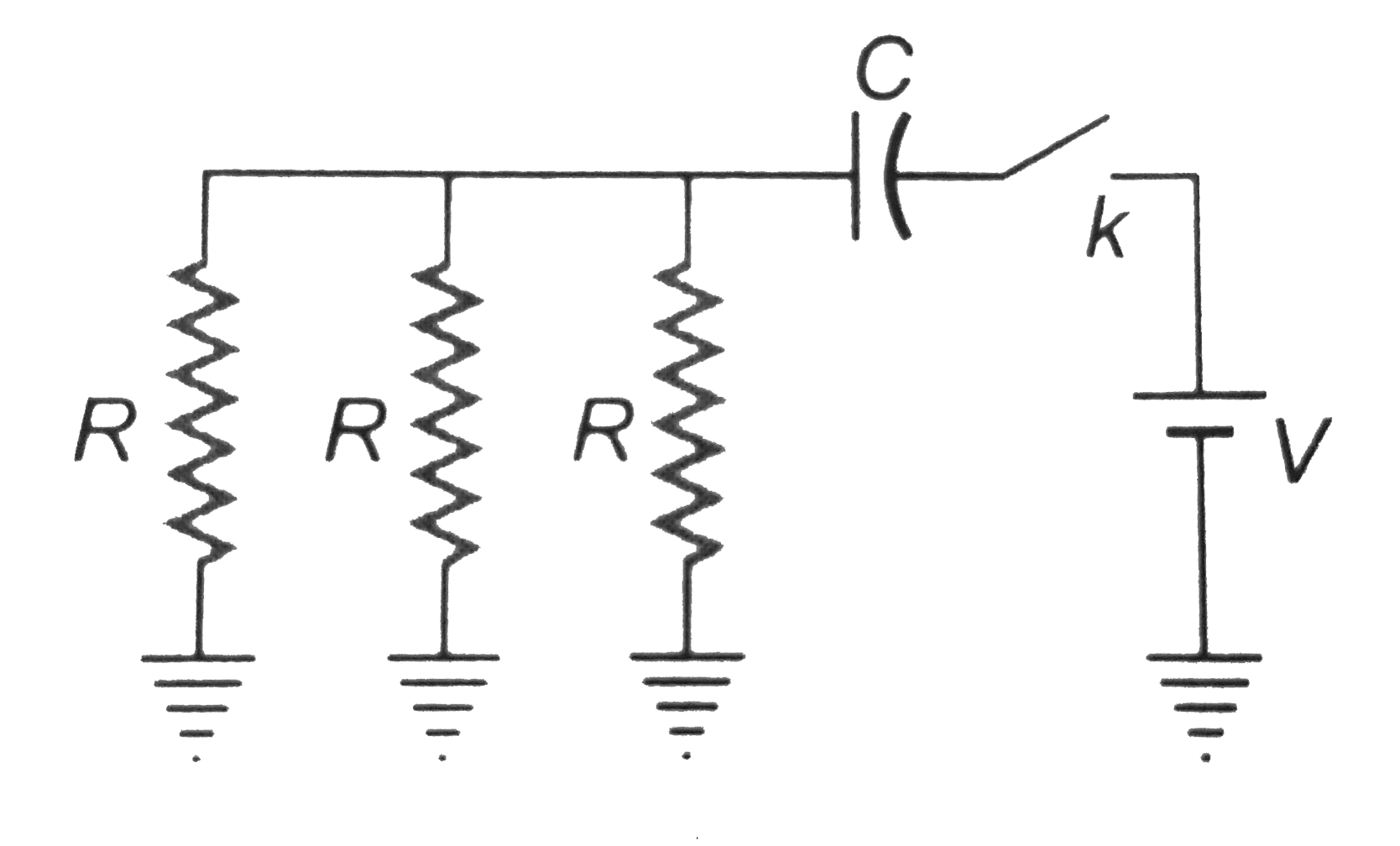
View SolutionThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
 View Solution
View Solution

