A wire shaped to a regular hexagon of side carries a current of . Find the magnetic field at the cetre of the hexagon.
To find the magnetic field at the center of a regular hexagon carrying a current, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon consists of six equal sides. Given that each side of the hexagon is 2 cm, we can visualize the hexagon and recognize that it can be divided into six equilateral triangles.
Step 2: Calculate the Radius to the Center
The distance from the center of the hexagon to the midpoint of any side (which we will call r) can be calculated using the properties of a 30-60-90 triangle. In a regular hexagon, the radius r can be found using the formula:
r=s√3
where s is the length of the side. Here, s=2cm=0.02m.
Calculating r:
r=0.02√3≈0.01155m
Step 3: Use the Formula for Magnetic Field
The magnetic field B at the center of the hexagon due to one side can be calculated using the formula for the magnetic field due to a straight current-carrying conductor:
B=μ0I4πrsinθ
where:
- μ0=4π×10−7T m/A (permeability of free space),
- I=2A (current),
- r is the distance from the center to the wire,
- θ=30∘ (angle between the line from the center to the wire and the perpendicular to the wire).
Step 4: Calculate sinθ
For θ=30∘:
sin30∘=12
Step 5: Substitute Values into the Formula
Substituting the values into the magnetic field formula for one side:
B=(4π×10−7)×24π×0.01155×12
Step 6: Calculate the Magnetic Field for One Side
Simplifying the equation:
B=(4π×10−7)×24π×0.01155×2
B=10−70.01155≈8.66×10−6T
Step 7: Calculate Total Magnetic Field
Since there are six sides contributing to the magnetic field at the center, the total magnetic field Btotal is:
Btotal=6×B
Btotal=6×(8.66×10−6)≈5.196×10−5T
Final Answer
The magnetic field at the center of the hexagon is approximately:
Btotal≈6.9×10−5T
A regular hexagon consists of six equal sides. Given that each side of the hexagon is 2 cm, we can visualize the hexagon and recognize that it can be divided into six equilateral triangles.
The distance from the center of the hexagon to the midpoint of any side (which we will call r) can be calculated using the properties of a 30-60-90 triangle. In a regular hexagon, the radius r can be found using the formula:
r=s√3
where s is the length of the side. Here, s=2cm=0.02m.
r=0.02√3≈0.01155m
The magnetic field B at the center of the hexagon due to one side can be calculated using the formula for the magnetic field due to a straight current-carrying conductor:
B=μ0I4πrsinθ
where:
- μ0=4π×10−7T m/A (permeability of free space),
- I=2A (current),
- r is the distance from the center to the wire,
- θ=30∘ (angle between the line from the center to the wire and the perpendicular to the wire).
For θ=30∘:
sin30∘=12
Substituting the values into the magnetic field formula for one side:
B=(4π×10−7)×24π×0.01155×12
Simplifying the equation:
B=(4π×10−7)×24π×0.01155×2
B=10−70.01155≈8.66×10−6T
Since there are six sides contributing to the magnetic field at the center, the total magnetic field Btotal is:
Btotal=6×B
Btotal=6×(8.66×10−6)≈5.196×10−5T
The magnetic field at the center of the hexagon is approximately:
Btotal≈6.9×10−5T
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - Exercise160videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of a regular hexagon of side 2√3 cm is
A18√3cm2B12√3cm2C36√3cm2D27√3cm2 - Question 2 - Select One
The area of a regular hexagon of side 2√3 cm is :
A18√3cm2B12√3cm2C36√3cm2D27√3cm2 - Question 3 - Select One
The area of a regular hexagon of side 2√3 cm is :
A18√3cm2B12√3cm2C36√3cm2D27√3cm2
A wire shaped to a regular hexagon of side x carries a current I ampere. Calculate the strength of the magnetic field at the centre of the hexagon.
View SolutionArea of a regular hexagon with side ‘a’ is
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
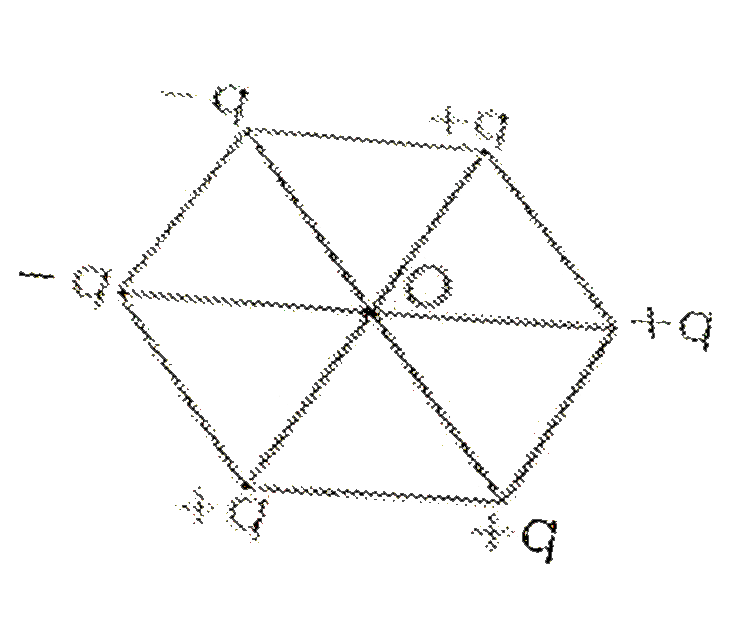
Find the magnitude of electric field at the centre of regular hexagon.View SolutionArea of regular hexagon with side 'a' is
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View Solution

