A wire shaped to a regular hexagon of side x carries a current I ampere. Calculate the strength of the magnetic field at the centre of the hexagon.
A
√3μ0Iπx
B
3μ0Iπx
C
μ0I3πx
D
μ0I√3πx
Text Solution
The correct Answer is:A
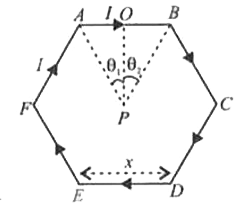
Let ABCDEF be a regular hexagon of side x m with its centre at P (figure). The magnetic field at P due to the current I (ampere) in the arm AB is given by
B=μ04π.Ia(sinθ1+sinθ2)
where a= OP
Here, θ1=θ2=30∘ (from the geometry of the figure), PB= AB=x and a = OP = PB cos30∘=x.√32
∴B=μ04π.Ix.√32(sin30∘+sin30∘)=μ04π.2I√3x(12+12
=μ02π.I√3x tesla.
The direction of B at point P is perpendicular to the plane of the page directed downward. Similarly, the magnetic fields at P due to the other arms of the hexagon, i.e, BC, CD, DE, EF and FA are same and act in the same direction. Therefore, the total magneitc field at P=6B=6×μ02π.I√3x=√3μ0Iπx tesla
acting in a direction perpendicular to the plane of the page direction downward.
|
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENTBOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions
22 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
- MAGNETICSBOOK - MTG-WBJEECHAPTER - MAGNETICSEXERCISE - WB JEE Previous Years Questions (Category 3: One or More than one Option)
2 Videos
Similar Questions
Knowledge Check
Area of a regular hexagon with side ‘a’ is
A3√34a2 sq. unitB122√3a2 sq. unitC92√3a2 sq. unitD6√2a2 sq. unitArea of regular hexagon with side 'a' is
A3√34a2 sq. unitB122√3a2 sq. unitC92√3a2 sq. unitD6√2a2 sq. unitSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
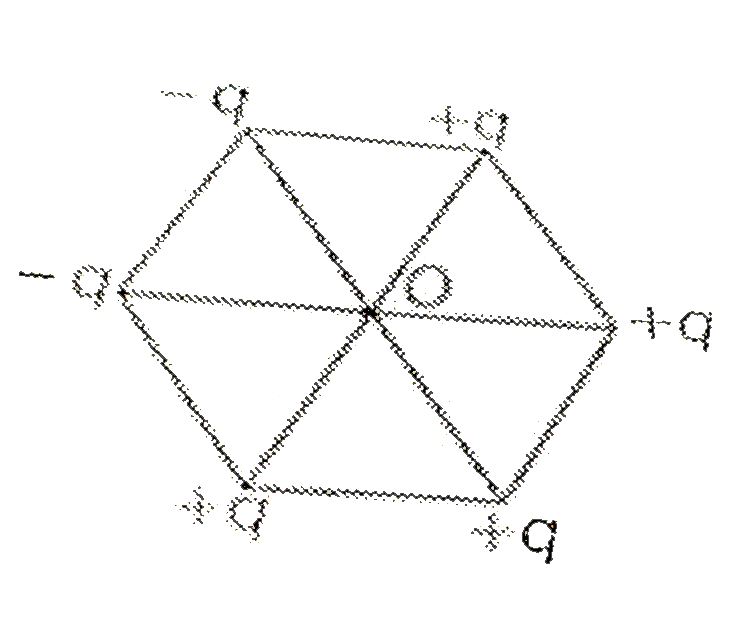
Find the magnitude of electric field at the centre of regular hexagon.Aq4πε0a2BzeroCq2πε0a2Dnone of these
A wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
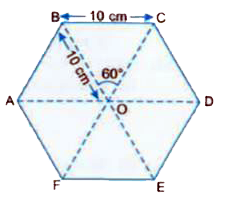
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
View SolutionA closed circuit is in the form of a regular hexagon of side r. If the circuit carries current I, what is the magnetic field induction at the centre of the hexagon?
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View Solution
