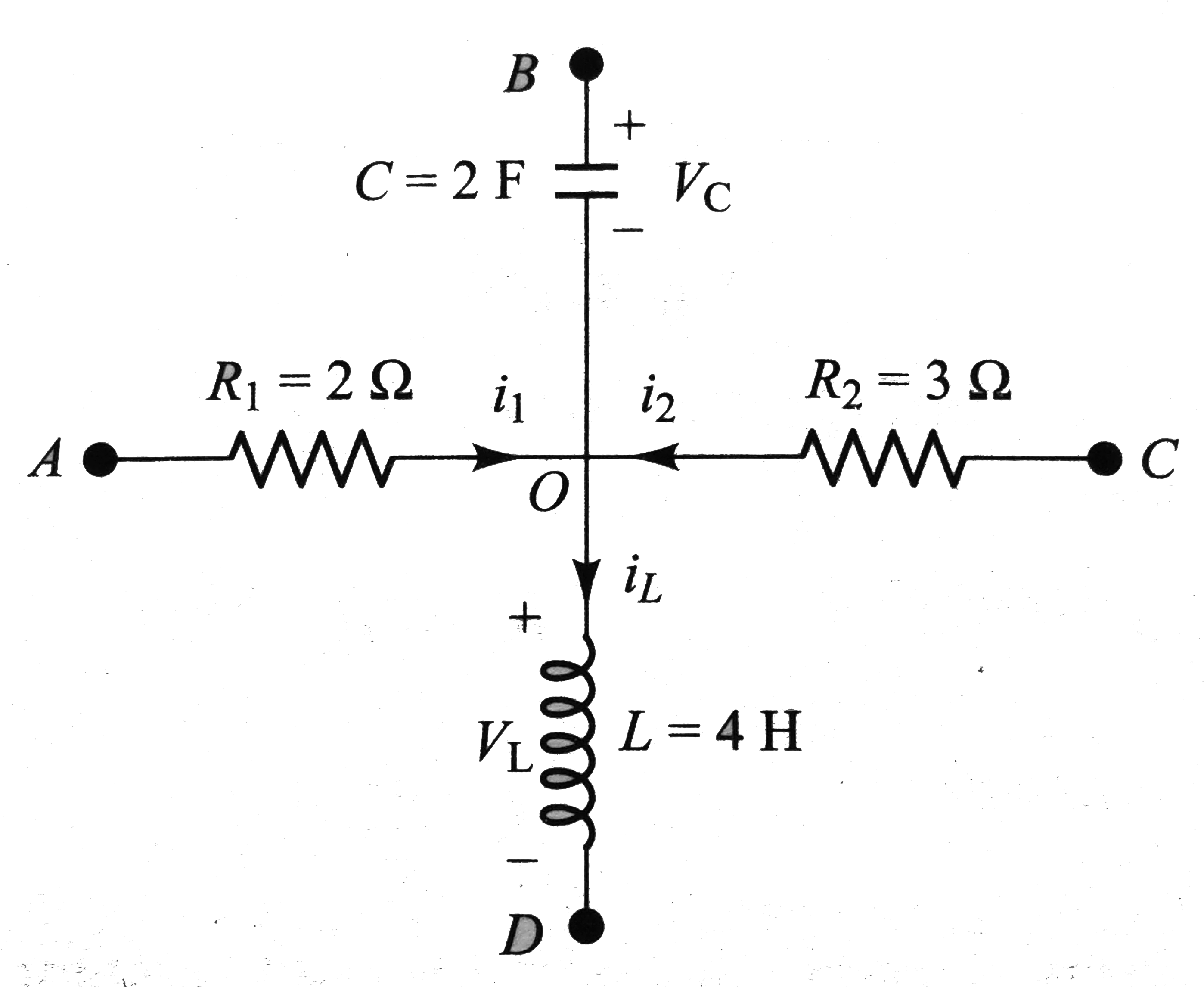
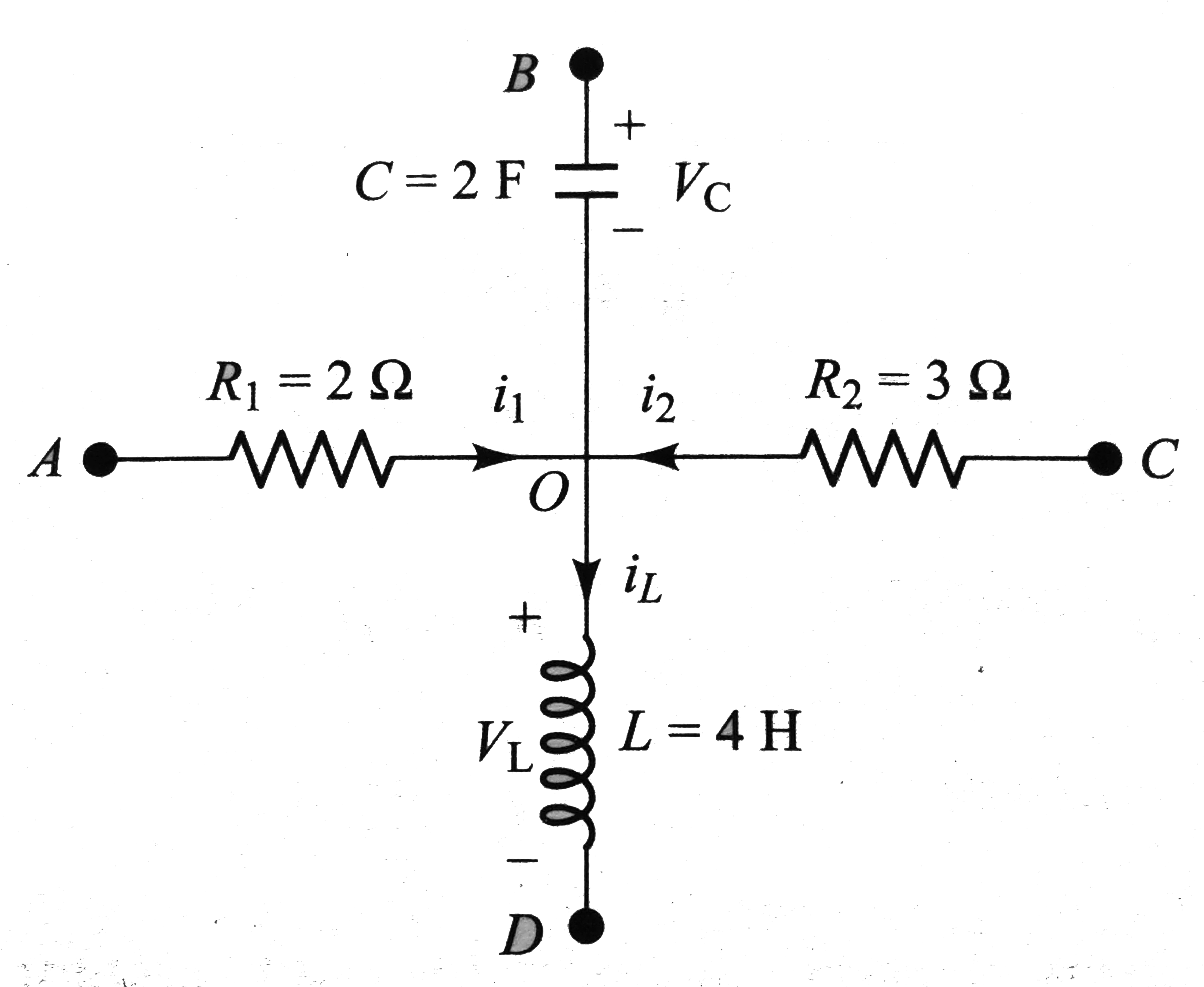
In the Figure shown i1=10e−2tA,i2=4A and VC=3e−2tV. Determine
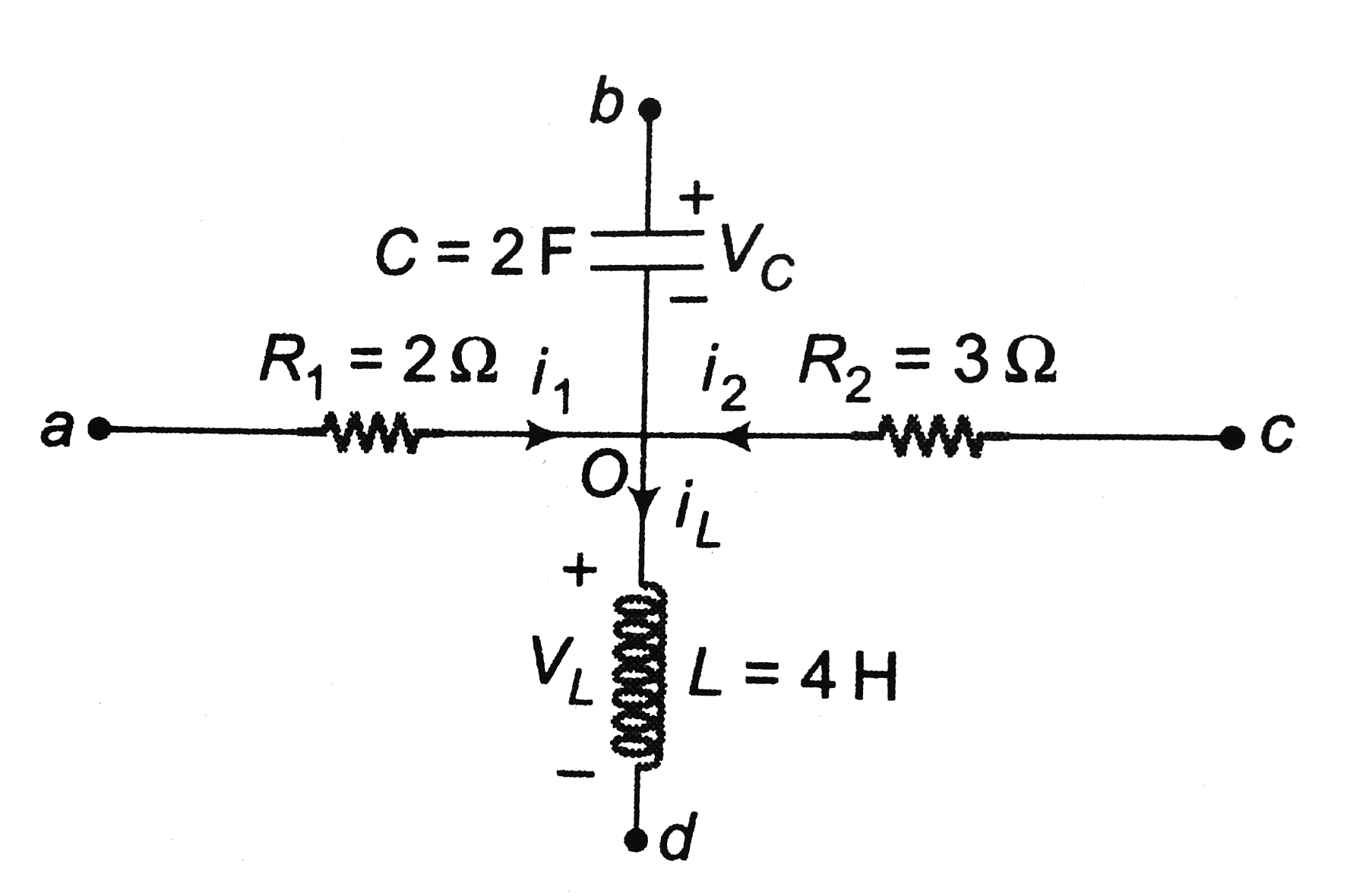
a. iL and VL b. Vac,Vab,Vcd
Video Solution
Text Solution
a. Charge stored in the capacitor at time t,
q=CVC
=(2)(3e−2t)
=6e−2tC
∴ic=dqdt=12e−2tA
(Direction of current is form b to O)
Applying junction rule at O,
iL=i1+i2+ie=10e−2t+4−12e−2t
=(4−2e−2t)A
[2+2(1−e−2t)]A
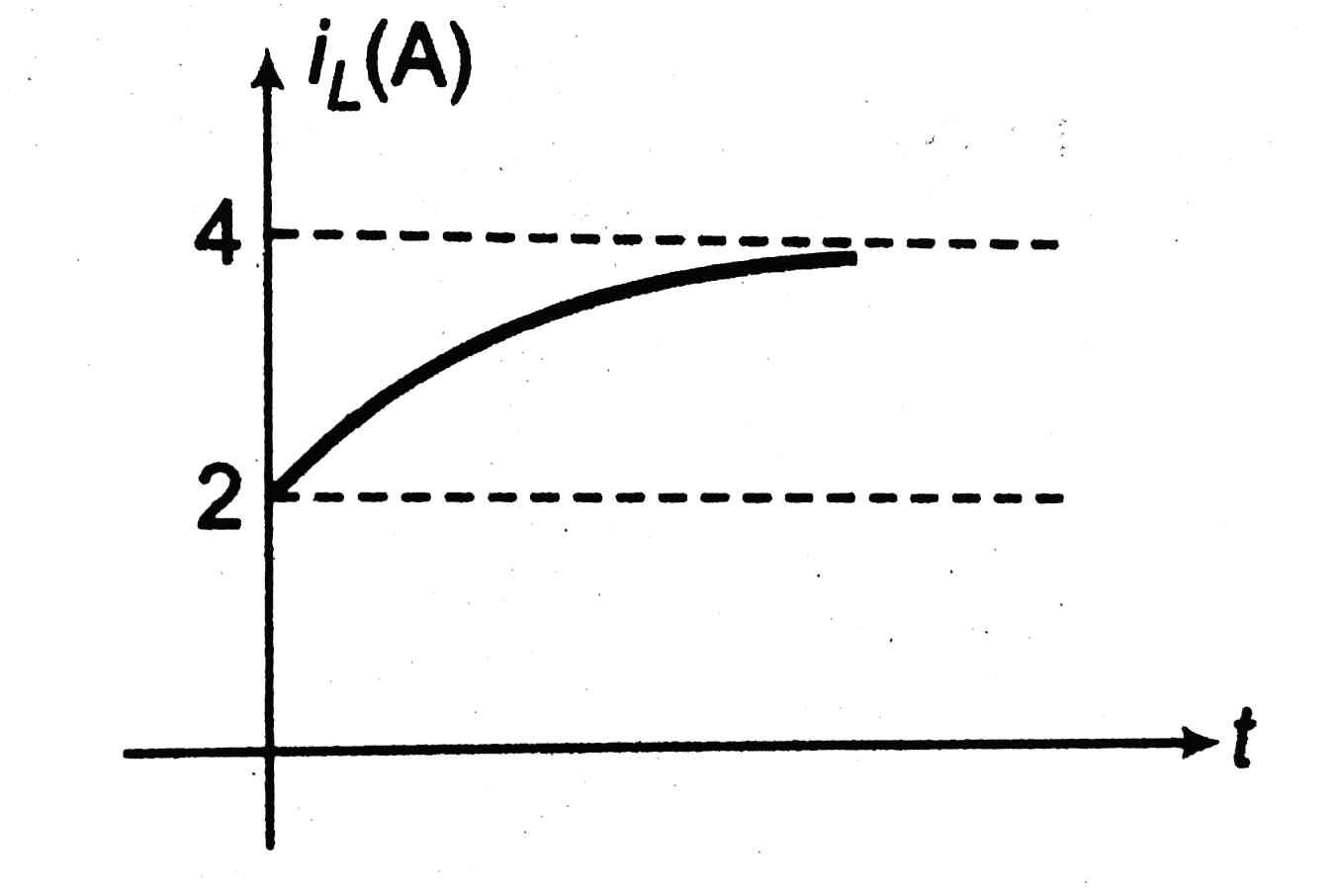
iL versus time graph is as show in figure.
iL increases from 2A to 4A exponentially .
VL=VOd=LdiLdt=(4)ddt(4−2−2t)
=16e−2tV
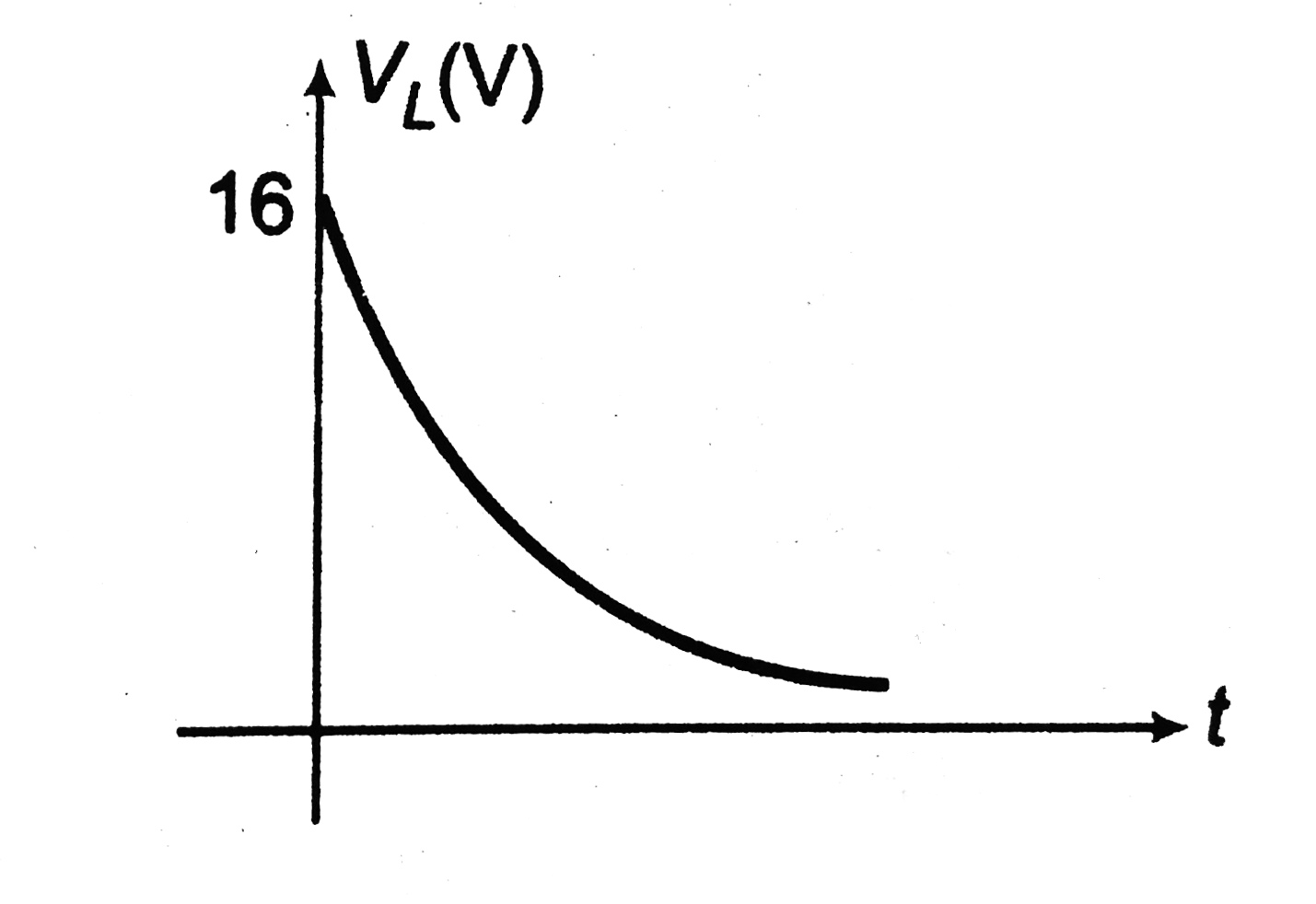
VL versus time graph is an shown in figure.
VL decreases exponentially from 16V to 0.
b. Vac=Va−Vc
Va−i1R1+i2R2=Vc
∴Va−Vc=Vac=i1R11−i2R2
substituting the values we have
Vac=(10e−2t)(2)−(4)(3)
Vac=(20e−2t−12)V
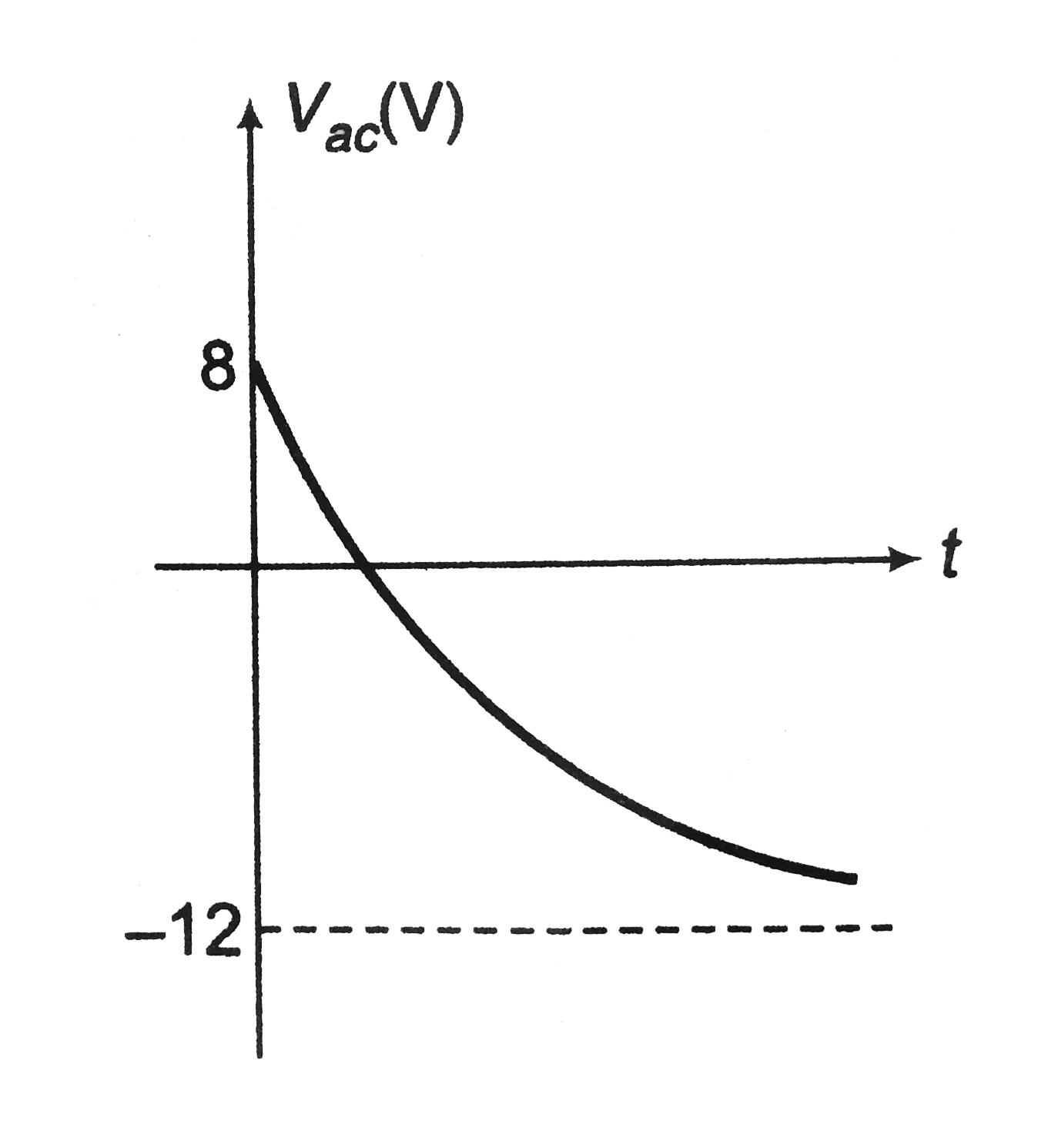
At t=0,Vac=8V and at t=∞,Vac=−12V
Therefore Vac decreases exponentially from 8 to −12V.
Vab=Va−Vb
Va−i1R1+VC=Vb
∴Va−Vb=Vab=i1R1−VC
Substituting the values , we have
Vab=(10e−2t)(2)=3e−2t
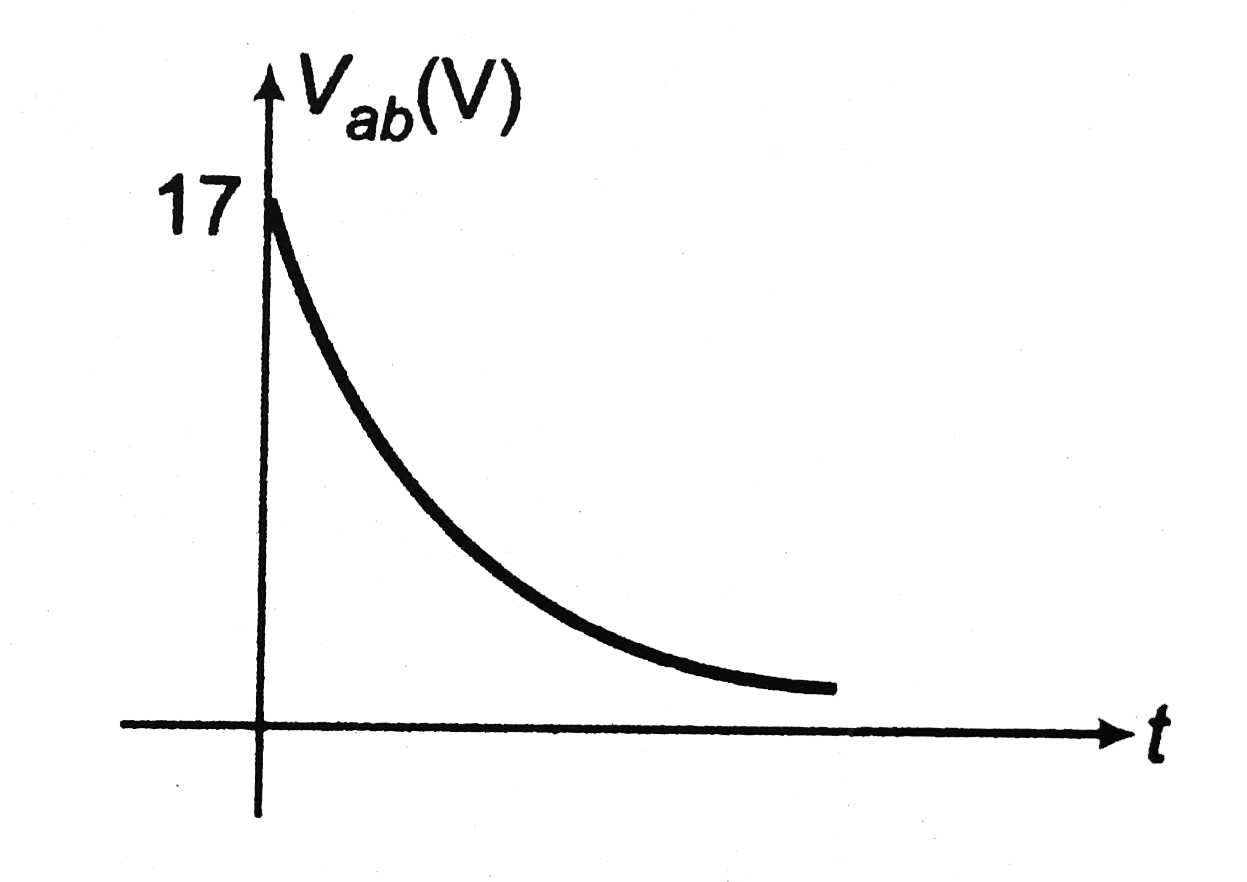
or Vab=17e−2tV
Thus Vab decreses exponentially from 17V to 0.
Vab versus t graph is shown in figure.
Vcd=VC−Vd
Vd−i2R2−VL=V4
∴Vc−Vd=Vcd=i2R2+VL
Substituting the values we have
Vcd=(4)(3)+16e−2t
Vcv=(12+16e−2t)V
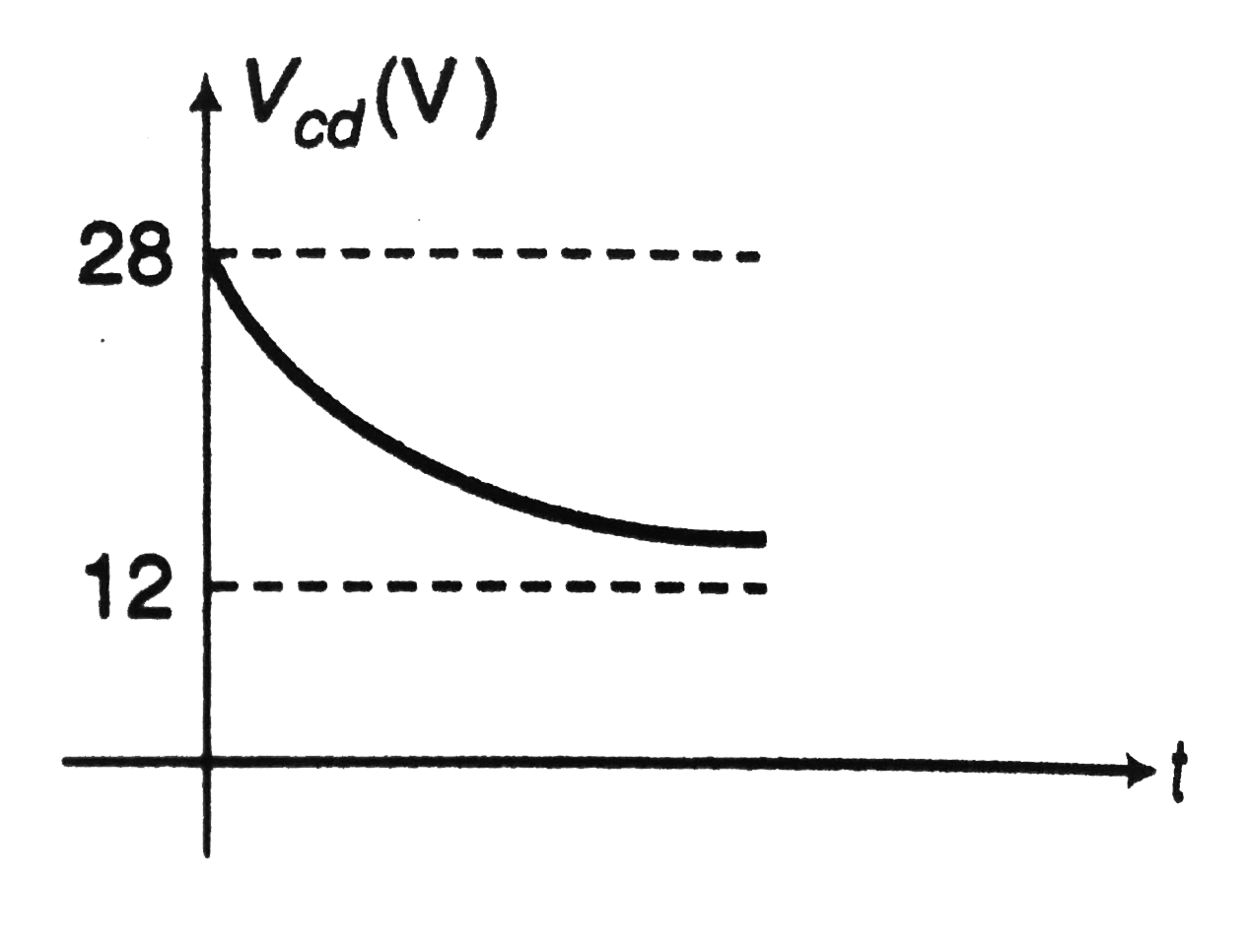
At t=0,Vcd=28 and at t=∞,Vcd=12V
i.e. Vcd decreases exponentially from 28V to 12V
Vcd versus t graph is shown in figure.

|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 3
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 4
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 1
3 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
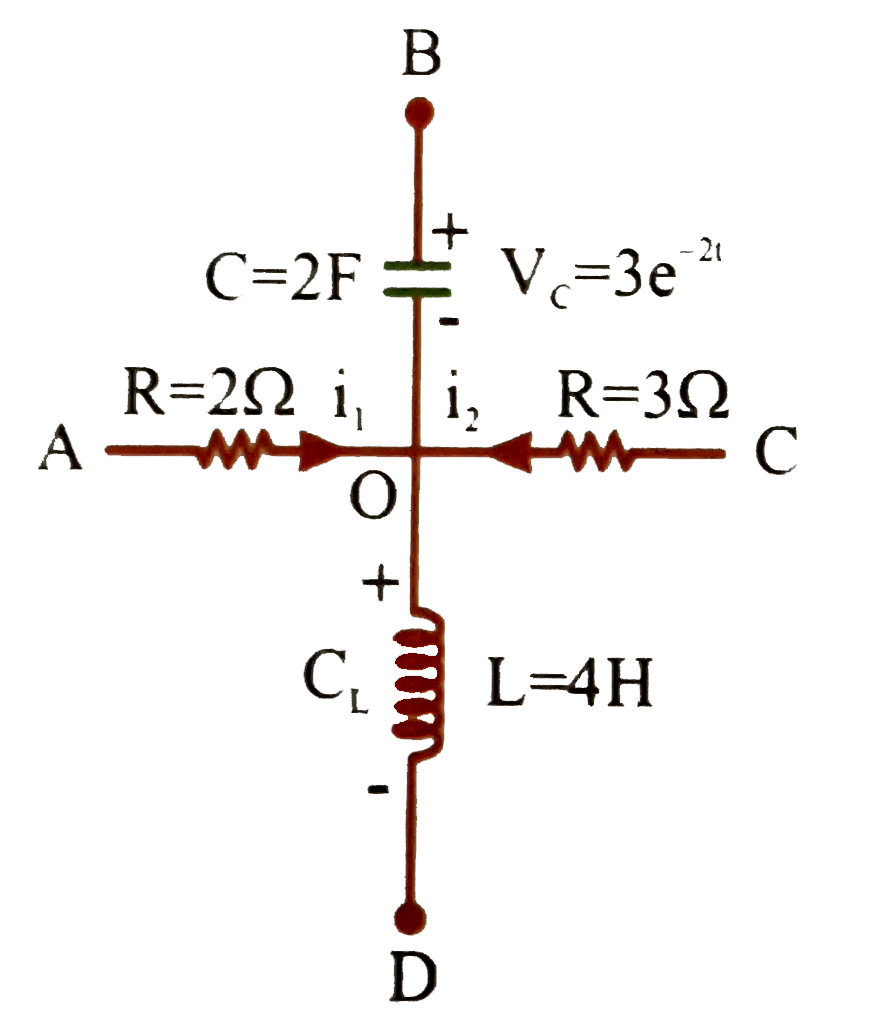
The current iL isA[2−2(1−e−2t)]AB[2+2(1−e−2t)]AC[3−2(1−e−2t)]AD[2+3(1−e−2t)]AIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
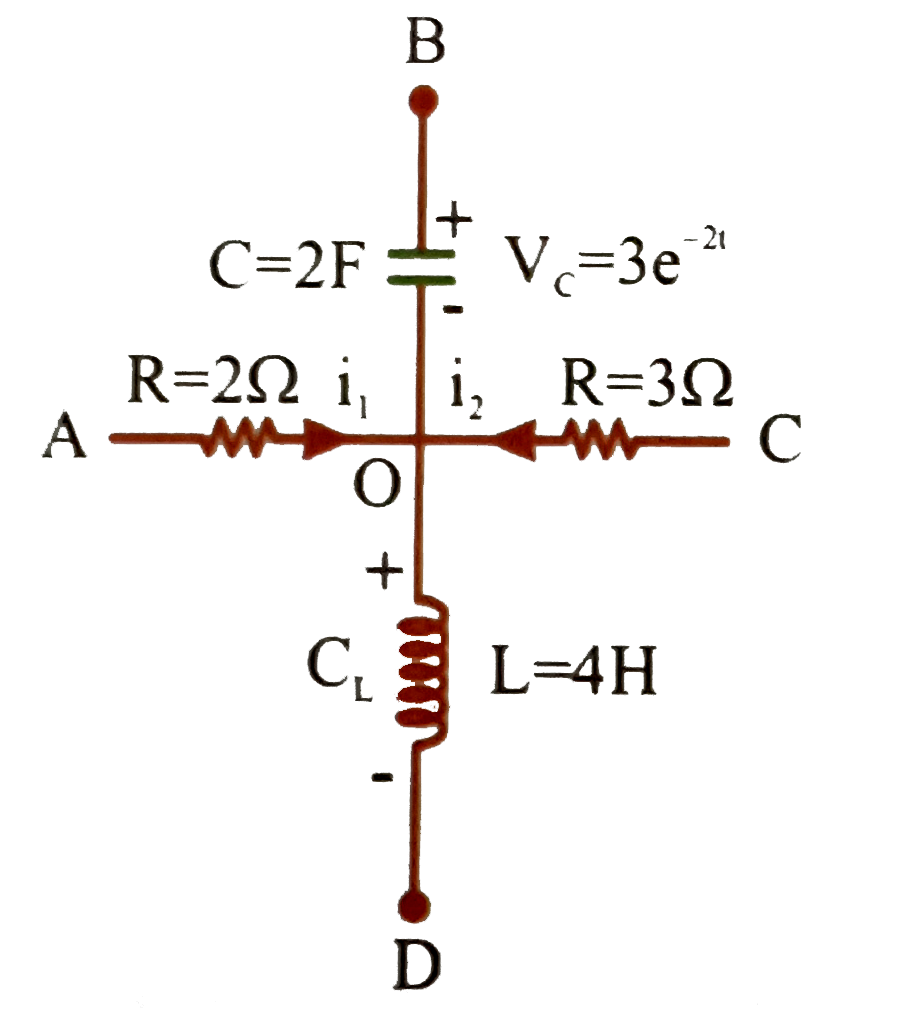
The potential difference across inductor VL is :A8e−2tVB9e−2tVC16e−2tVD18e−2tVIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
the vartiation of potential difference across A and C(VAC) with time can be respresented asA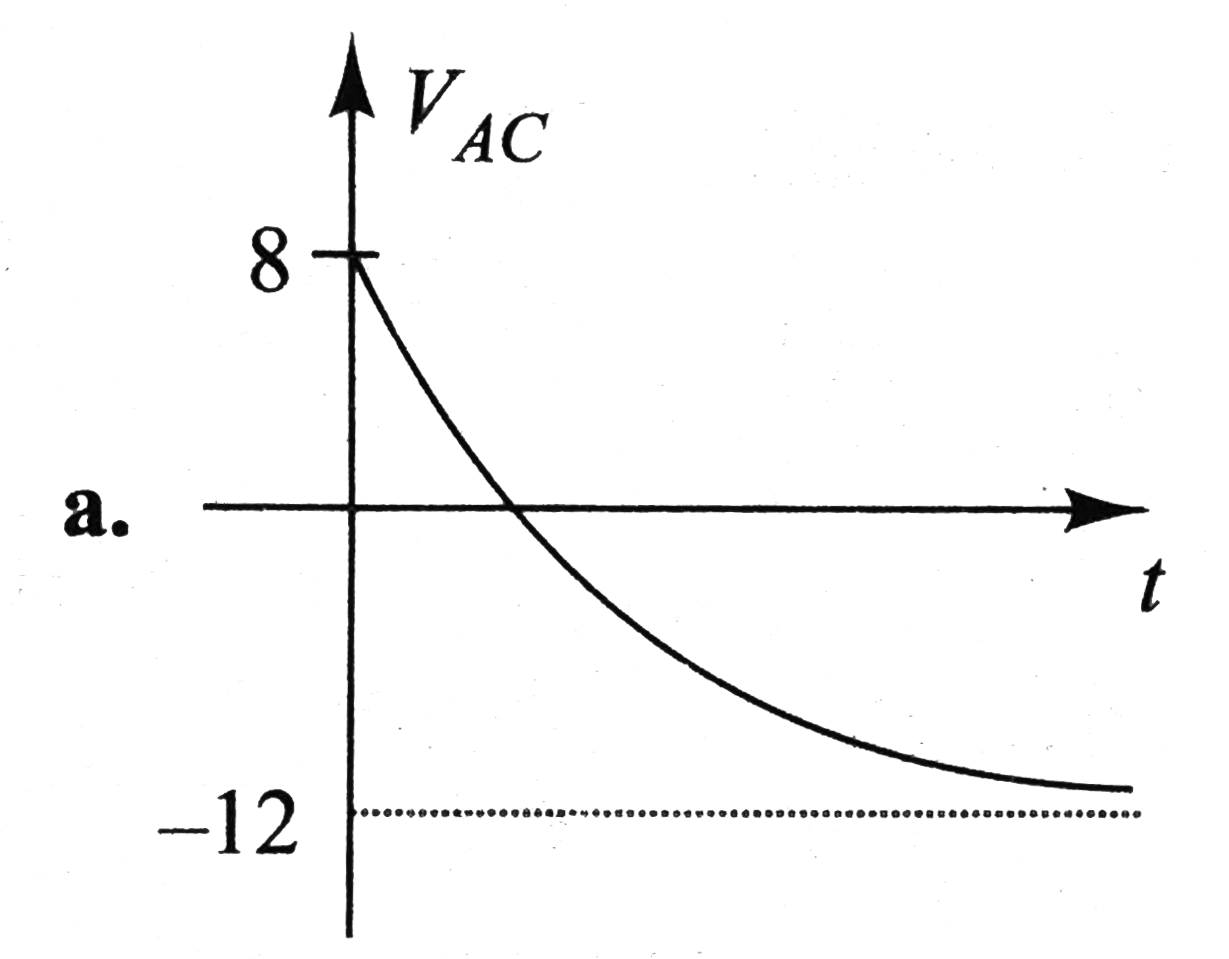 B
B C
C D
D
In the figure shown i=10e−41A. Find BLandVab

View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
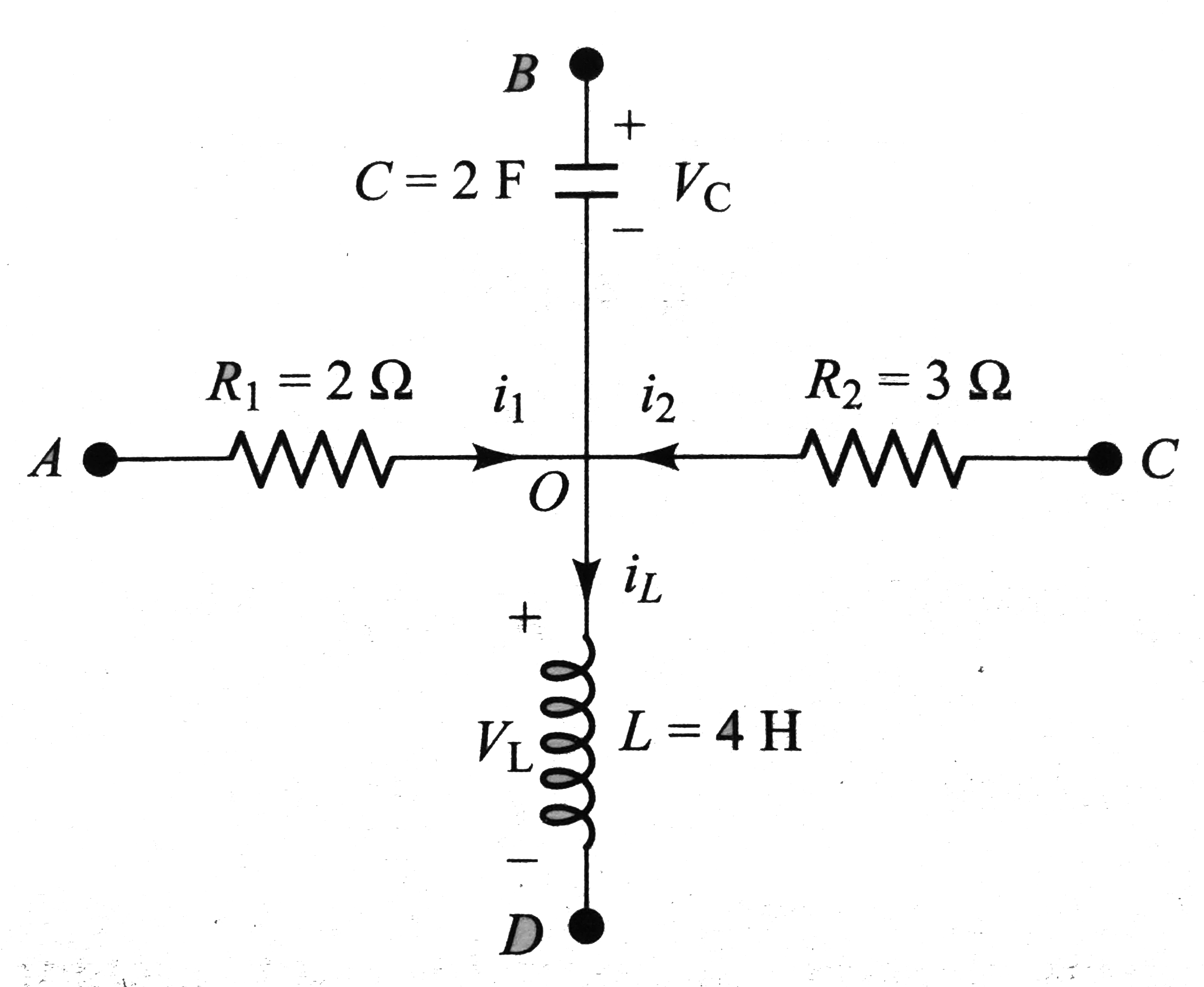
The variation of potential difference across C and D(VCD) with time can be expressed as
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
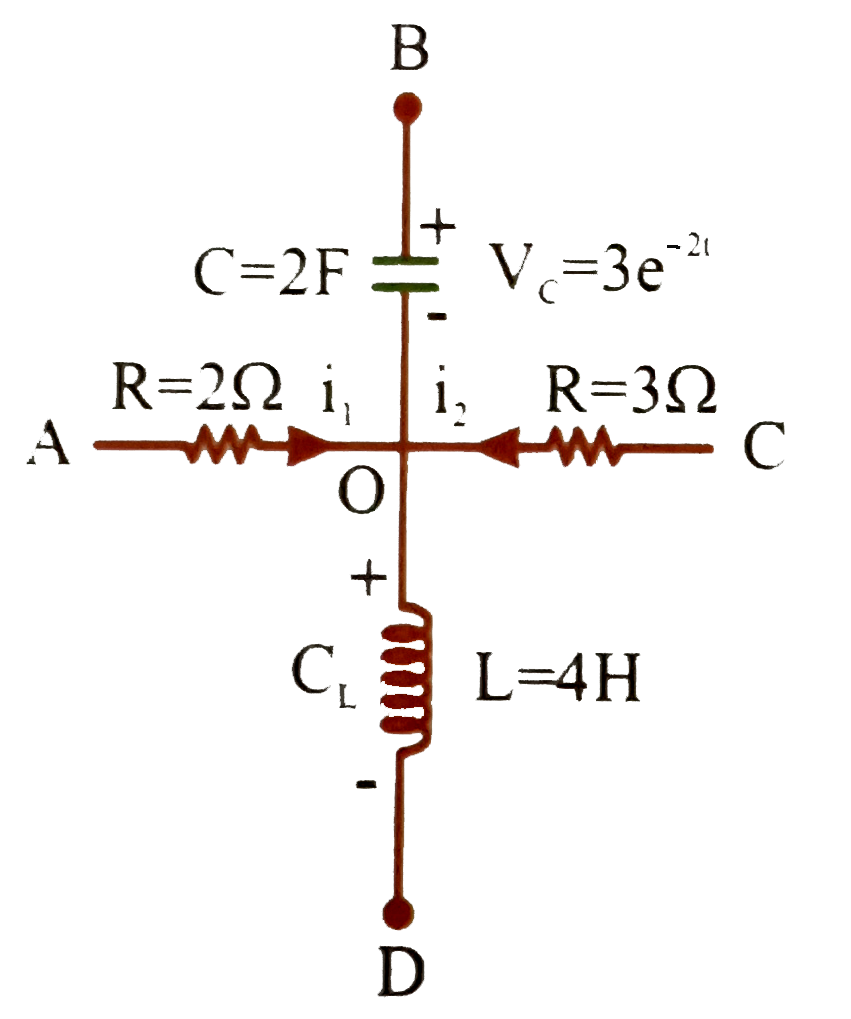
The potential difference across AB(VAB) is:
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
The variation of current in the inductor with time can be represented as
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
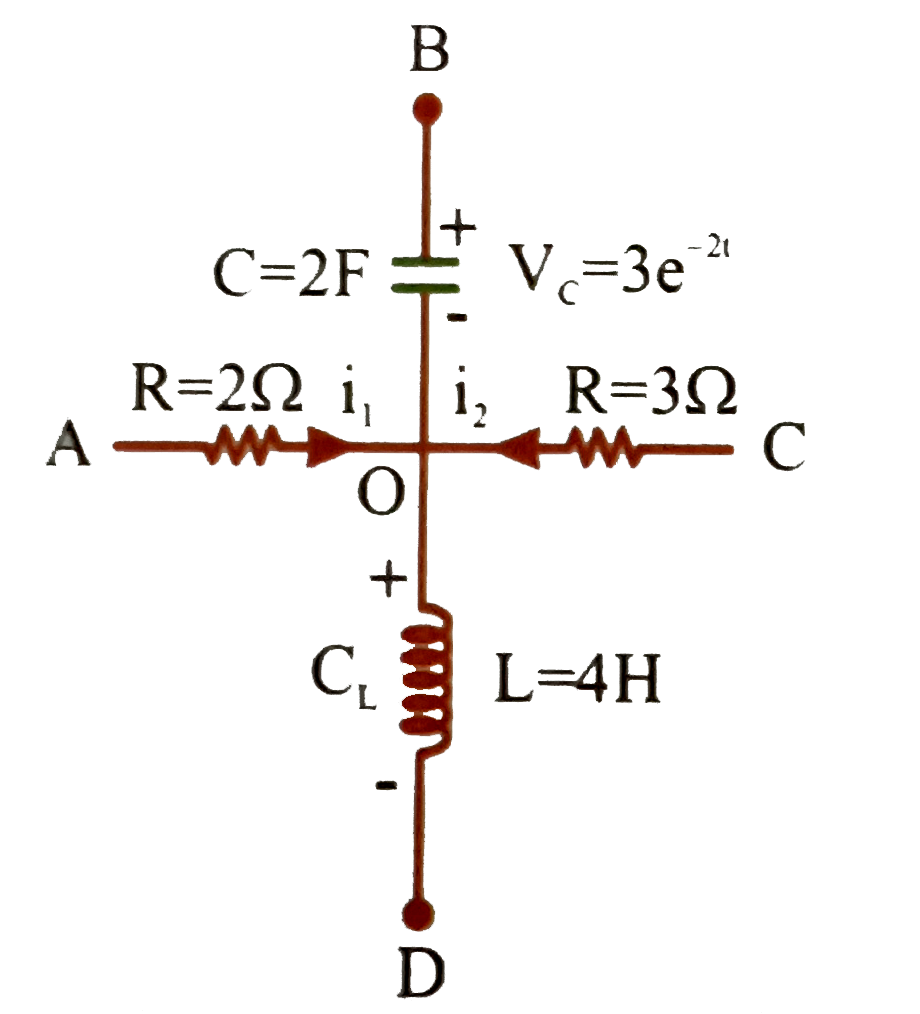
The variaton of current in the inductor with time can be repesented as :
View Solution


