In an L−C circuit, L=3.3H and C=840pF. At t=0 charge on the capacitor is 105μC and maximum. Compute the following quantities at t=2.0ms.
a. The energy stored in the capacitor.
b. The total energy in the circuit,
c. The energy stored in the inductor.
6.0J , 1.56J , 0.56
6.0J , 6.56J , 1.56
4.0J , 6.56J , 0.56
6.0J , 6.56J , 0.56
The correct Answer is:D
Given L=3.3H,C=840×10−12F and q0=105×10−6C
The angular frequency of L−C oscillations is
ω=1√LC=1√3.3×840×10−12
=1.9×104rad/s
Charge stored in the capacitor at time t would be
q=q0cosωt
a. At t=2×10−3s,
q=(105×10−6)cos[1.9×104][2×10−3]
=100.3×10−6C
∴ Energy stored in the capacitor,
UC=12q2C
=(100.3×10−6)22×840×10−12 ltbgt. =6.0J
b. Total energy in thhe circuit,
U=12q20C=(105×10−6)22×840×10−12
=6.56J
c. Energy stored in inductor in the given time
=total energy in circuit-energy stored in capacitor
=(6.56−6.0)J
=0.56J
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 5
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 6
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 3
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
The ratio of energy stored in capacitors C1 and C2
 A98B89C56D65
A98B89C56D65A capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
A2π√LCB12π√LCCπ√LC2D12π√LCIn the circuit shown in, C=6μF. The charge stored in the capacitor of capacity C is
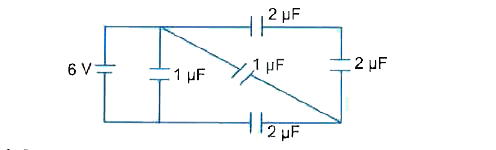
 . AzeroB90μCC40μCD60μC
. AzeroB90μCC40μCD60μC
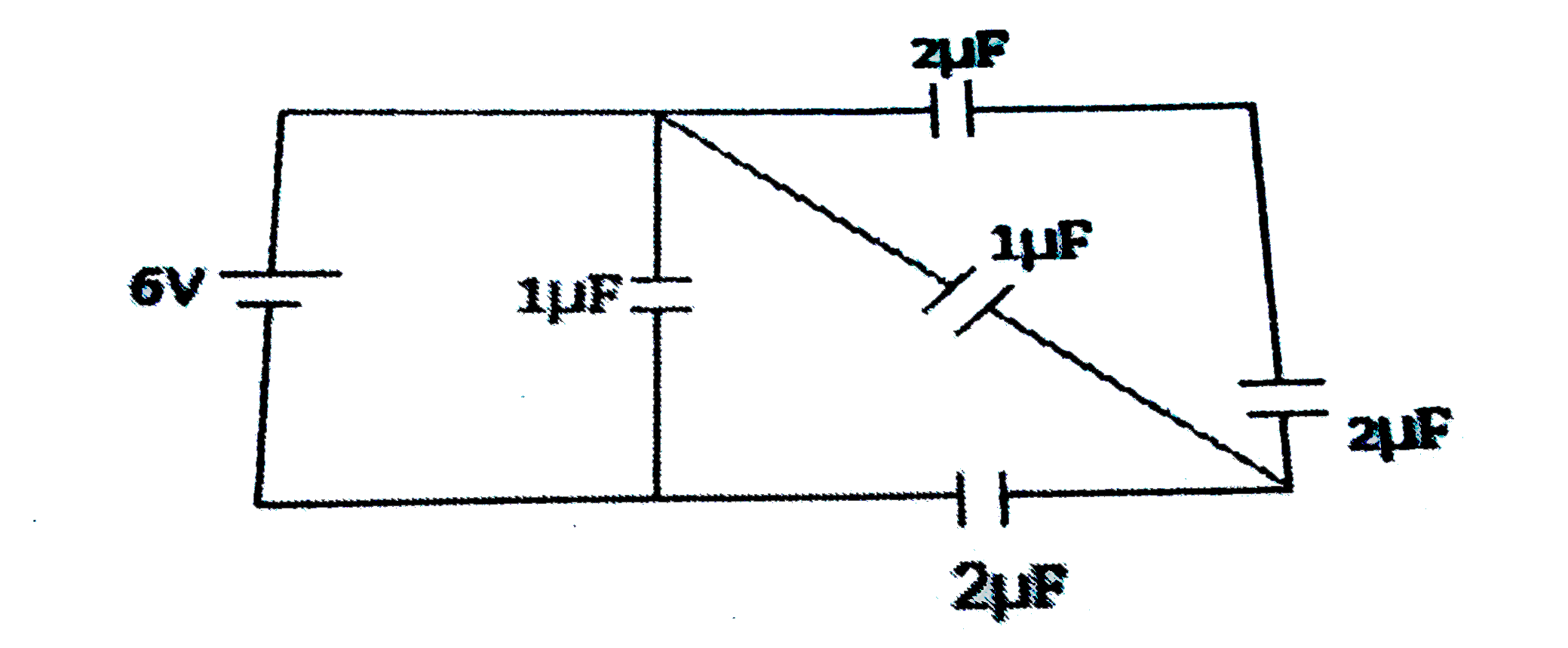
(a) Find charge on capacitors

(b) Find charge on capacitor
(c ) Find energy stored in capacitor.
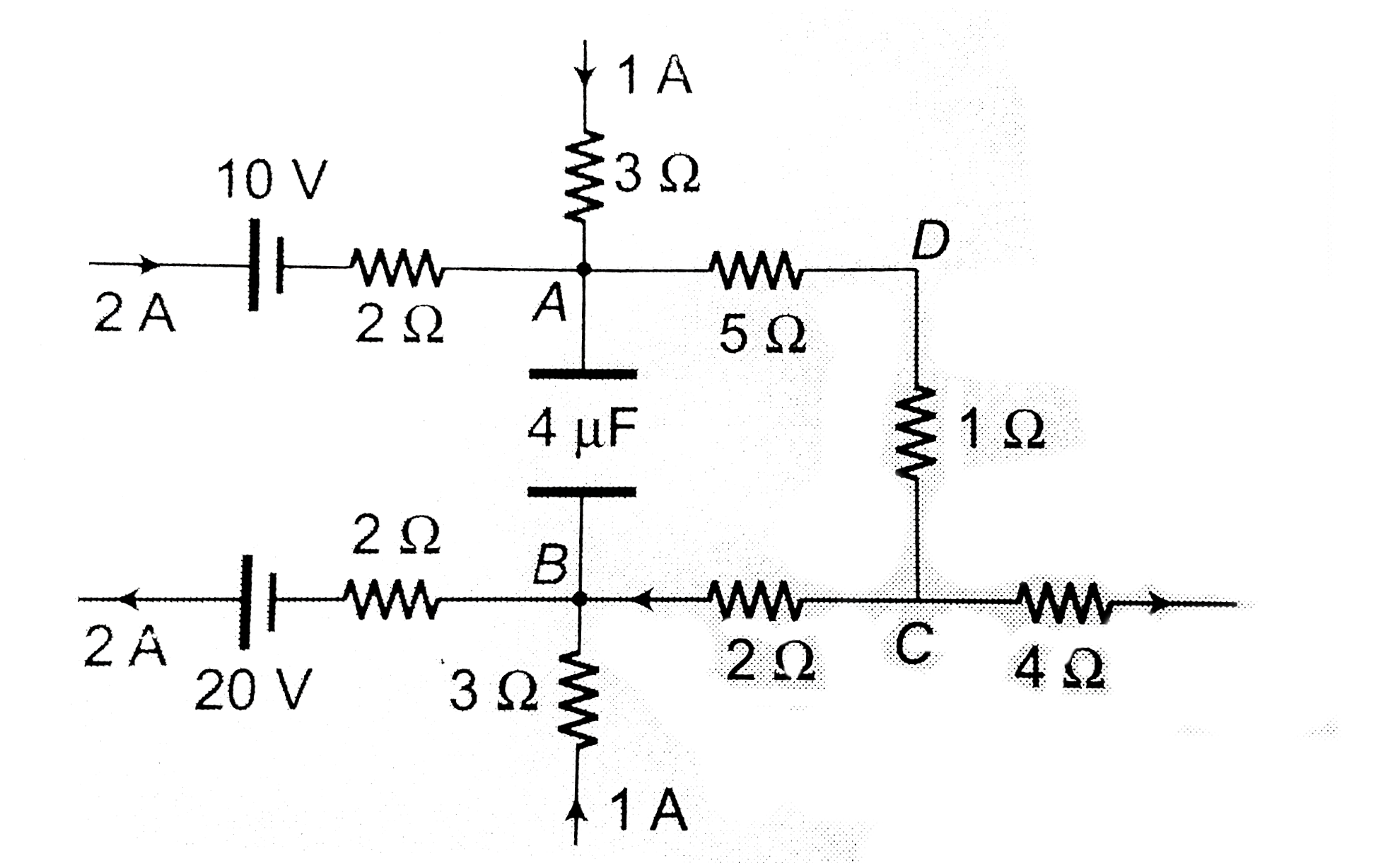
View SolutionIn an oscillating LC circuit, L = 3.00 mH and C = 3.90 μF. At t=0 the charge on the capacitor is zero and the current is 1.75 A. (a) What is the maximum charge that will appear on the capacitor? (b) At what earliest time t > 0 is the rate at which energy is stored in the capacitor greatest, and (c) what is that greatest rate?
View Solution
Find currents I1,I2 and I3 and the energy stored in the capacitors C1andC2 in the circuit shown in figure.
View SolutionIn an oscillating LC circuit, L = 25.0 mH and C = 2.89 μF. At time t=0 the current is 9.20 mA, the charge on the capacitor is 3.80 μC and the capacitor is charging. What are (a) the total energy in the circuit, (b) the maximum charge on the capacitor, and (c) the maximum current? (d) If the charge on the capacitor is given by q= cos(ωt+ϕ), what is the phase angle ϕ? (e) Suppose the data are the same, except that the capacitor is discharging at t= 0. What then is ϕ ?
View SolutionIn the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 10000.

View Solution