An inductor of inductance s connected across a charged capacitor of capacitance and the resulting circuit is set oscillating at its natural frequency. Let denote the instantaneous charge on the capacitor and the current in the circuit. It is found that the maximum value of charge is .
a. When , what is the value of ?
b. When , what is the value of ?
c. Find the maximum value of .
d. When is equal to one-half its maximum value, what is the value of ?
When , what is the value of
When what is the value of ?
Find the maximum value of .
When is equal to one-half of its maximum value, what is the value of ?
This is a problem oscillations.
Charge stored in the capacitor oscillates simple harmonically as
Here maximum value of
Let at then
........i
and ........ii
............iii
a.
or at
or
At from eqn iii:
b. or when i.e. ........
At the time
or
c.
Maximum value of is
d. From energy conservation
or
or
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 52videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 63videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 34videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
An inductor of inductance 2.0mH is connected across a charged capacitor of capacitance 5.0μF and the resulting L−C circuit is set oscillating at its natural frequency. Let Q denote the instantaneous change on the capacitor and i the current in the circuit. It is found that the maximum value of Q is 200μC .
(a) When Q=100μC , what is the value of |di/dt| ?
(b) When Q=200μC , what is the value of i ?
(c)Find the maximum value of i
(d) When i is equal to one-half its maximum value, what is the value of |Q| ?View SolutionAn inductor of inductance 20 mH is connected across a charged capacitor of capacitance 5 μF & resulting L-C circuit is set oscillating at its natural frequency . The maximum charge q is 200 μ C on the capacitor . Find the potential difference across the inductor when the charge is 100 μC .
View Solution
Knowledge Check
- Question 1 - Select One
An inductor of inductance 2.0 mH is connected across a charged capacitor of capacitance 0.5μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. it is found that the maximum value of charge Q is 200μC. what is the maximum value of I (in ampere)?
A1AB1.5AC2AD3A - Question 2 - Select One
An inductor of inductance 2 mH is connected across a charged capacitor of capacitance 5μF and the L-C circuit is set oscillating at its natural frequency. What is the natural angular frequency of its oscillations?
A2×103rad/sB104rad/sC2×104rad/sD0.5×105rad/s - Question 3 - Select One
A non-resistive inductor is connected across a fully charged capacitor and the L-C circuit is set oscillating at its natural frequency. What is the value of the current when the charge on the capacitor has the maximum value of 100μC?
AZeroBInfinityC10μAD100μA
An inductor of inductance 2 mH is connected across a charged capacitor of 5 μ F . Let q denote the instaneous charge on the capacitor and i the current in the circuit . Maximum value of q is Q = 200 μ C.
(a) When q = 100 μ C what is the value of /di/dt / ?
(b) When q = 200 μ C what is the value of i ?View SolutionAn inductance of 1mH and a charged capacitor capacitance of 10 mu F are connected across each other.The resonating angular frequency of circuit is
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
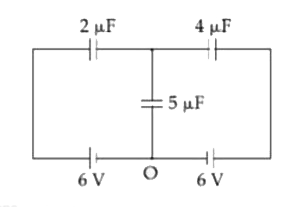 View Solution
View SolutionDetermine the charge on the capacitor in the following circuit in μC ________.
 View Solution
View SolutionThe charge on the 6 μF . Capacitor in the circuit shown is
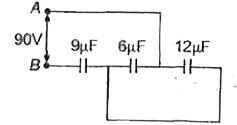 View Solution
View Solution

